ПРОЕКТ на тему «Путешествие в историю математики»

Муниципальное автономное общеобразовательное учреждение

«Белоярская средняя общеобразовательная школа №1»

Белоярского городского округа

ПРОЕКТ

на тему «Путешествие в историю математики»

п. Белоярский

2022 г.

СОДЕРЖАНИЕ

Введение…………………………………………………………………………………..3

• Проблемный вопрос

• Цель

• Задачи

• Методы исследования

Глава 1: ТЕОРЕТИЧЕСКАЯ…………………………...……………………………...4

1.1. История возникновения математики как науки.

1.2. Знаменитые математики древности.

Глава 2: ПРАКТИЧЕСКАЯ…………………………………………………………...10

2.1. Стенд «История возникновения математики».

2.2. Процесс создания стенда.

2.3. анкетирование.

Вывод…………………………………………………………………………….............14

Заключение……………………………………………………………………………...14

Источники информации………………………….….…….…………………………..15

ВВЕДЕНИЕ

Математика – точная дисциплина, которую называют царицей всех наук. Принято считать, что первые числа появились тысячи лет тому назад, вместе с речью. По этому поводу Ф. Энгельс писал, что самый древний источник математических знаний – это пальцы рук. Среди самых древних математических документов, дошедших до наших дней, считают записи вавилонян. По оценкам ученых, они сделаны более восьми тысяч лет назад. Математические записи встречаются и у других народов. Так как появилась математика, и кто ее придумал?

Проблемный вопрос:

В нашей школе нет стенда по истории математики

Цель – создание информационного стенда по истории математики.

Задачи:

1. Изучить историю возникновения математики.

2. Провести анкетирование среди обучающихся школы.

3. Разработать дизайн информационного стенда.

4. Подобрать теоретический материал для его заполнения.

5. Создать стенд.

Методы исследования:

• Поиск и анализ источников информации в сети Интернет.

• Практический метод.

• Опрос.

Продукт проекта:

Стенд «История возникновения математики»

ГЛАВА 1. Теоретическая.

1.1. История возникновения математики.

Никто точно не может сказать, как появилась математика. Сведения о ней содержатся в разных письменах у различных народов. Самые древние сведения, дошедшие до наших дней – клинописные таблички. Найденные артефакты эпохи Вавилона показывают, что даже шесть тысяч лет тому назад люди вели подсчеты домашних расходов, торговых сделок, решали математические задачки. Позже вавилоняне начали решать сложные алгебраические задачки, кубические и квадратные вычисления. А как появилась математика с дробями, когда это было? Такие сложные действия люди научились вычислять не сразу, однако уже в Древнем Египте умели проводить вычисления с дробями, у которых в числителе была единица. Десятичные дроби появились благодаря самаркандскому математику Гияс-ад-дин Джамшид ибн Масуд аль-Каши пятьсот лет назад. Спустя почти два столетия фламандский математик Стивен ввел их в Европе. Даже сегодня в математике совершаются различные открытия. Это связано с тем, что математика – наука, которая не стоит на месте, а постоянно движется вперед.

1.2 Первые открытия

Многие ученые пытаются разгадать загадку истории – как появилась математика. Однако точную дату возникновения науки никто не может назвать. Среди всех существующих открытий, самое значимое – изобретение самого числа и четырех основных действий: сложения, вычитания, деления и умножения. Среди геометрических понятий, первыми достижениями стали прямая и окружность. Далее огромный вклад в развитие науки внесли вавилоняне и египтяне примерно три тысячи лет назад. Исходя из этого, отвечая на вопрос, где появилась математика, можно сказать, что она зародилась в Вавилоне, а затем в Египте. Сохранившиеся таблички показывают, какие вычисления проводились в те времена.

1.3 История о математике

Ученые все еще задаются вопросом, в какой стране появилась математика. Есть свидетельства, показывающие, что простые измерения проводились у инков. Этот народ разработал особую узелковую систему счета, которая позволяла вести подсчеты доходов и расходов. Из Древнего Египта до нас дошли тексты решения задач. Египтяне знали дроби, проводили расчеты площадей, объемов. Одному из документов более четырех тысяч лет – это папирус Ринда. Из библиотеки Ашшурбанипала до нас дошли глиняные таблички. Междуречье считалось высокоразвитым. Здесь даже математика была более высокого уровня, чем в других странах. Не малый вклад в развитие науки сделали древние греки. Около трехсотого года до нашей эры, Евклидий создал манускрипт, посвященный геометрии. Позже вклад в науку внесли другие ученые. В Китае, примерно в двухсотом году до нашей эры, изучали математику по «Арифметике в девяти главах». Это писание было составлено на основе ранних записей.

1.4 Математики древности

Пифагор

Пифагору традиция приписывает введение слов «философия» и «философ». На вопрос «Кто он таков?» Пифагор ответил: «философ», что означает «любомудр». Жизнь для Пифагора была подобна игрищам: «иные приходят на них состязаться, иные — торговать, а самые счастливые — смотреть; так и в жизни иные, подобные рабам, рождаются жадными до славы и наживы, между тем как философы — до единой только истины».

Современные исследователи выделяют две составляющие в учении Пифагора: научный подход к познанию мира и религиозно-мистический образ жизни. Личные заслуги Пифагора в первой части доподлинно неизвестны, так как позднее ему приписывали всё, созданное последователями в рамках школы пифагореизма. Вторая часть превалирует в учении Пифагора, и именно она осталась в сознании большинства античных авторов. Изначально пифагористов делили на «математиков» и «акусматиков». Первые изучали всю суть науки, вторые — лишь получали обобщённый свод знаний в виде «акусм» (устных предписаний). После смерти Пифагора среди его последователей сформировались два течения — математиков (пифагорейцев) и «акусматиков» (пифагористов). Пифагористы с помощью акусм строили свою жизнь. Их учение состояло в повторении изречений Пифагора, к которым они относились как к божественным предписаниям. Они не стремились к созданию чего-либо нового и развитию учения, а считали мудрыми тех, кто усвоил и может применять в повседневной жизни наибольшее количество подобных, приписываемых Пифагору, изречений.

Архимед

Работы Архимеда относились почти ко всем областям математики того времени: ему принадлежат исследования по геометрии, арифметике, алгебре. Он нашёл все полуправильные многогранники, которые теперь носят его имя, значительно развил учение о конических сечениях, дал геометрический способ решения кубических уравнений вида {\displaystyle x^{2}(a\pm x)=b}x^{2}(a\pm x)=b, корни которых он находил с помощью пересечения параболы и гиперболы. Архимед провёл и полное исследование этих уравнений, то есть нашёл, при каких условиях они будут иметь действительные положительные различные корни и при каких корни будут совпадать.

Однако главные математические достижения Архимеда касаются проблем, которые сейчас относят к области математического анализа. Греки до Архимеда сумели определить площади многоугольников и круга, объём призмы и цилиндра, пирамиды и конуса. Но только Архимед нашёл гораздо более общий метод вычисления площадей или объёмов; для этого он усовершенствовал и виртуозно применял метод исчерпывания Евдокса Книдского. В своей работе «Послание к Эратосфену о методе» (иногда называемой «Метод механических теорем») он использовал бесконечно малые для вычисления объёмов. Идеи Архимеда легли впоследствии в основу интегрального исчисления.

Эратосфен

Из сочинений Эратосфена по математике до нашего времени дошло только написанное к царю Птолемею письмо об удвоении куба. Это письмо сохранилось в комментарии Евтокия к трактату Архимеда «О шаре и цилиндре». В письме содержатся некоторые исторические сведения о делийской задаче, а также описание прибора, изобретённого самим автором и известного под именем мезолябия.

Сведения о других математических сочинениях Эратосфена отличаются крайней неполнотой. Папп в двух местах своего «Собрания» называет сочинение Эратосфена «О средних величинах», замечая при этом, что оно во всех своих предположениях стоит в связи с линейными местами.

О сочинении Эратосфена «Платоник», посвящённом пропорциям, говорит Теон Смирнский. Возможно, что именно к Эратосфену восходит алгоритм «разворачивания всех рациональных отношений из отношения равенства», описанный Теоном Смирнским и Никомахом Герасским.

Отрывок из ещё одного сочинения Эратосфена приводит во «Введении в арифметику» Никомах Герасский. То же делает и Ямвлих в своём комментарии к этому сочинению Никомаха. Предмет этого отрывка состоит в изложении найденного Эратосфеном способа определения произвольного количества последовательных простых чисел (так называемое решето Эратосфена). Название «решето» метод получил потому, что во времена Эратосфена писали числа на дощечке, покрытой воском, и прокалывали дырочки в тех местах, где были написаны составные числа. Поэтому дощечка являлась неким подобием решета, через которое «просеивались» все составные числа, а оставались только числа простые

Аристотель

Аристотель считал предметом математики «количественную определенность и непрерывность». В его трактовке «количеством называется то, что может быть разделено на составные части, каждая из которых… является чем-то одним, данным налицо. То или другое количество есть множество, если его можно счесть, это величина, если его можно измерить». Множеством при этом называется то, «что в возможности (потенциально) делится на части не непрерывные, величиною то, что делится на части непрерывные». Прежде чем дать определение непрерывности, Аристотель рассматривает понятие бесконечного, так как «оно относится к категории количества» и проявляется прежде всего в непрерывном. «Что бесконечное существует, уверенность в этом возникает у исследователей из пяти оснований: из времени (ибо оно бесконечно); из разделения величин..; далее, только таким образом не иссякнут возникновение и уничтожение, если будет бесконечное, откуда берется возникающее.

ГЛАВА 2. Практическая.

ПОДВЕДЕНИЕ ИТОГОВ:

Среди учеников был проведен опрос. (62 участника)

Каждый ученик ответил на следующие вопросы:

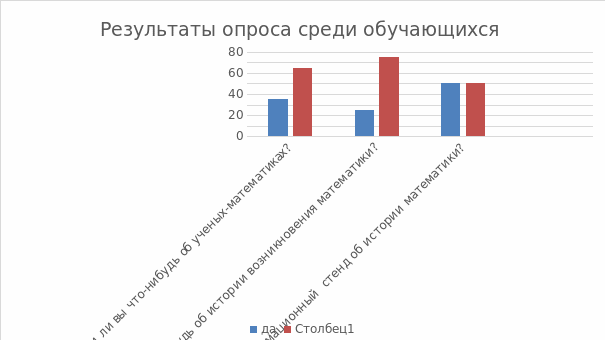
Вывод по опросу: большинство учеников ничего не слышали об ученых-математиках, а также не знают об истории возникновения математики.

Также половина учеников хотели бы видеть стенд об истории математики, а другая нет.

ВЫВОД:

В результате работы над проектом мне удалось добиться поставленной цели. Я изучил историю возникновения математики. На основе изученного материала создал стенд. Провёл опрос МАОУ «Белоярской СОШ № 1».

В ходе мастер-класса я познакомил школьников с изготовлением математической головоломки и предложил решить её. Провел опрос, из которого узнал, что большинству школьников моя головоломка понравилась, её смысл был всем понятен. Также многие ребята считают, что она может быть полезна для их развития. А вот придумать что-то подобное ребята считают сложным.

Я считаю, что всё задуманное было выполнено. Наиболее интересным этапом работы для меня был процесс изготовления математической головоломки. Особых трудностей в работе над проектом я не испытывал. Времени на выполнение работы было достаточно

В процессе работы над проектом я научился ориентироваться в различных источниках информации и обрабатывать ее, определять цель и задачи своей работы, планировать собственную деятельность, подводить итоги.

ЗАКЛЮЧЕНИЕ:

Некоторые головоломки известны с глубокой древности. Оригинальные логические задачи находят на стенах египетских пирамид, в древнегреческих манускриптах и в других исторических памятниках. В настоящее время на рынке появляются новые игры, конструкции и издания, призванные держать интеллект человека в тонусе, развивать логику, тренировать нестандартное мышление и повышать интеллектуальный уровень в целом.

Изготовленное мною изделие может пригодится учителям математики для внеурочных занятий с учениками, школьникам для развития интереса к математике.

ИСТОЧНИКИ ИНФОРМАЦИИ

1. Головоломка — Википедия [Электронный ресурс]. – Режим доступа: https://ru.wikipedia.org/wiki/Головоломка – (Дата обращения 12.12.21).

2. История появления головоломок, пазлов и кроссвордов [Электронный ресурс]. – Режим доступа: https://logictoys.ru/blog/posts/istoriya-golovolomok – (Дата обращения 12.12.21).

3. История появления головоломок, их создание и развитие [Электронный ресурс]. – Режим доступа: https://solunsun.ru/istoriya-poyavleniya-golovolomok/ – (Дата обращения 12.12.21).

4. Игра в 15 — Википедия [Электронный ресурс]. – Режим доступа: https://ru.wikipedia.org/wiki/Игра_в_15 – (Дата обращения 12.12.21).

5. Судоку — Википедия [Электронный ресурс]. – Режим доступа: https://ru.wikipedia.org/wiki/Судоку – (Дата обращения 12.12.21).

6. Танграм — Википедия [Электронный ресурс]. – Режим доступа: https://ru.wikipedia.org/wiki/Танграм – (Дата обращения 12.12.21).

7. Кубик Рубика — Википедия [Электронный ресурс]. – Режим доступа: https://ru.wikipedia.org/wiki/Кубик_Рубика – (Дата обращения 12.12.21).