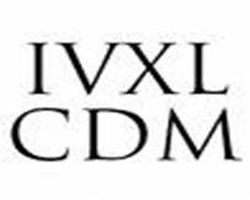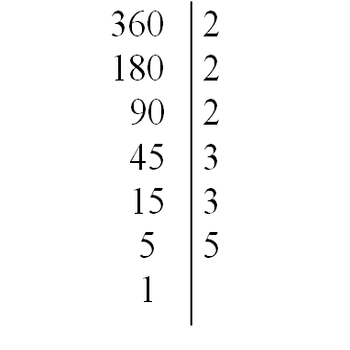Проект "Натуральные числа"

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «ЗЕРНОВСКАЯ СЕДНЯЯЯ ШКОЛА»

САКСКОГО РАЙОНА РЕСПУБЛИКИ КРЫМ

ПРОЕКТ

по математике

НАТУРАЛЬНЫЕ ЧИСЛА

Работу выполнил:

обучающийся 9 класса Умеров Владимир Владимирович

Руководитель: Ягьяева Арина Геннадьевна,

учитель математики

ЗЕРНОВОЕ, 2021

Содержание

Введение
Глава 1. Натуральные числа.
1.1. Причины возникновения натуральных чисел.
1.2. Системы счисления.
Глава 2. Действия над натуральными числами и их свойства.
2.1. Свойства сложения и вычитания.
2.2. Умножение натуральных чисел и его свойства.
2.3. Делимость натуральных чисел и его свойства.
2.4. Простые и составные числа.
Глава 3. Занимательные факты о натуральных числах.
Заключение
Список использованной литературы

Введение

Для счета предметов используются числа 1,2,3,4,5 и т.д. Такие числа подходят для подсчета яблок в вазе, грузовиков в гараже, учебников в классе. Кроме того, они используются для измерения величин: длины, площади, массы, времени, скорости. Но числа появляются не только тогда, когда мы считаем предметы или единицы измерения. Подсчитывать приходиться и многое другое: количество рейсов самолетов между городами, уроков математики в учебном году, глав в книге и т.д.

Для таких чисел используют специальное название – натуральные числа.

В рамках школьной программы история математики изучается поверхностно. Мы мало знаем о происхождении тех или иных терминах и математических понятиях. Понятие натуральных чисел не имеет чёткого и безупречного определения, но математики долгое время опираются на него при определении других важных понятий. Кажется, что человеку всегда приходилось складывать, вычитать, умножать и делить, т.е. числа всегда сопровождали человека по жизни. Но как появились первые натуральные числа, почему они возникли, и какую роль играют в жизни человека?

На эти вопросы я попытался ответить в своей работе.

Я поставил перед собой цели:

1. Выяснить, как сформировалась у людей первое представление о натуральных числах, как оно изменялось с развитием науки математики.

2. Изучить необычные и ранее неизвестные факты о натуральных числах.

3. Изучить теоретический материал по теме работы.

Для достижения поставленных целей необходимо было решить следующие задачи:

1. Ознакомиться с литературой о натуральных числах.

2. Обобщить полученные знания в своей работе.

Объект: натуральные числа.

Предмет: математические действия с натуральными числами.

Глава 1. Натуральные числа

1.1.Причины возникновения натуральных чисел

Натуральные числа – это первая числовая система, с которой встречается человек в своей жизни. Простейший вид чисел - натуральные числа - исторически возник из потребностей счета: одна лодка, два человека, три дерева и т.д.

Лишь на достаточно высоком интеллектуальном уровне было осознано, что у конкретных предметных групп "два камня", "две птицы" и "две руки" есть нечто общее: "два". Абстрактные, отвлеченные числа позволяли сравнивать количество предметов в разных группах, что имело важное значение при обменных операциях типа "раковина за орех".

Число - важнейшее понятие математики. Потребовалось несколько тысячелетий, чтобы это понятие приобрело тот вид, который в настоящий момент признается удовлетворительным для большинства математиков. Однако в соответствующих формулировках используется профессиональный язык такого высокого уровня, что попытка передать их точный смысл "простыми и понятными словами" безнадежна. Приходится довольствоваться лишь общими описаниями.

Числа 1,2,3,4,5,6,7,8,9, использующиеся для счета предметов или для указания порядкового номера того или иного предмета среди однородных предметов, называют натуральными.

1.2. Системы счисления

Развитие счета шло параллельно с изменением в психологическом восприятии понятия "много". Вначале было "один, два, много" или "один, два, три, много", но постепенно граница отодвигалась, формировался натуральный ряд чисел: 1, 2, 3, 4 и т.д.

Пальцы на руках установили первый предел счёта: десять. Принцип группировки по десять позволял охватывать все большие количества предметов, объединяя их в новые единицы счета: десять десятков - сотня, десять сотен - тысяча, дальше десяти тысяч обыденный разум не заглядывал. Так сформировалась десятичная система счисления.

Числа 1,2,3,4,5,6,7,8,9,0 – эти числа называются арабскими.

В древности числа записывали палочками: II - один, IIIII - пять, IIIIIIIIII- десять и т.п. Но это было неудобно, и люди искали и находились другие, каждый раз все более современные способы записи чисел. В Западной Европе вплоть до XVIII века в официальных документах применялась римская буквенная нумерация.

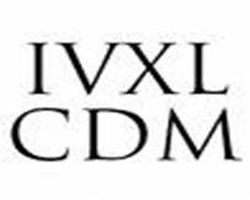
Числа записывали при помощи букв латинского алфавита: I-1, V-5, X-10, L-50, C-100, D-500, M-1000. Число также записывалось в виде последовательности цифр, но из эстетических соображений запрещалось четырехкратное повторение одной и той же цифры. Так что числа 4, 9, 40, 90, 400, 900 обозначались соответственно как IV, IX, XL, XC, CD, CM,- меньшая по значению цифра оказывалась левее большей (но часовщики упорно писали на циферблатах IIII, чтобы не путать с шестеркой VI).

В настоящее время римские цифры обычно применяются при нумерации глав и разделов книги, месяцев года, для обозначения дат, порядковых номеров, значительных событий, годовщины.

В наше время почти все народы пользуются счётом десятками, сотнями, тысячами, то есть десятичной системой счисления. В ней значение цифры зависит от позиции, которое оно занимает в записи числа. Поэтому такую систему счисления называют позиционной. В тёплых странах Африки и Америки, где люди ходили босыми, для счёта применялись не только пальцы рук, но и пальцы ног.

Для чтения многозначных чисел их разбивают, начиная справа, на группы по три цифры в каждой (самая левая группа может состоять из одной или двух цифр). Эти группы называют классами. Три первые цифры справа составляют класс единиц, три следующие – класс тысяч, далее идут классы миллионов, миллиардов и т. д.

Миллион – это тысяча тысяч (1000 тыс.), его записывают 1 млн или 1 000 000.

Миллиард – это 1000 миллионов. Его записывают 1 млр или 1 000 000 000. Чтобы прочитать число, называют слева по очереди число единиц каждого класса и добавляют название класса. Не произносят название класса единиц, а также класса, все три цифры которого – нули.

Немало различных способов записи чисел было создано людьми. В Древней Руси числа обозначали буквами с особым знаком «-» (титло), который писали над буквой. Первые девять букв алфавита обозначали единицы, следующие девять букв – десятки, а последние 9 букв – сотни. Число 10 тысяч называли словами «тьма» (и теперь мы говорим: народу – тьма тьмущая).

Современная достаточно простая и удобная десятичная система записи чисел была заимствована европейцами у арабов, которые в свою очередь переняли у индусов. Поэтому цифры, которыми мы считаем, пользуемся, европейцы называют «арабскими», а арабы – «индейскими». Эта система была введена в Европе примерно в 1120 году английским учёным – путешественником Аделардом.

К 1600 году она была принята в большинстве стран мира. Русские названия чисел тесно связаны с десятичной системой счисления. Например, пятнадцать означает «пять на десять», пятьдесят – «пять десятков», а пятьсот – «пять сотен».

Глава 2. Действия над натуральными числами и их свойства

2.1. Свойства сложения и вычитания

Для натуральных чисел определены операции сложения и умножения, причём сумма и произведение являются также натуральными числами. Натуральные числа можно складывать. Числа, которые складывают, называются слагаемыми. Число, получающееся при сложении этих чисел, называется их суммой. Сложить числа 2+5 – значит прибавить к числу 2 5раз единицу. Получим 2+5=2+1+1+1+1+1=3+1+3=7, короче 2+5=7.

Справедливы следующие свойства сложения натуральных чисел:

Переместительное свойство – это когда сумма чисел не изменяется при перестановке слагаемых.

Например: 2+8=10, 8+2=10.

Сочетательное свойство – это когда нужно прибавить к числу сумму 2х чисел. Надо сначала прибавить I слагаемое, а потом к полученной сумме – второе слагаемое.

Например: 2+(5+3)=2+8=10

(2+5)+3=7+3=10.

Натуральные числа также можно вычитать. Вычитание – это действие, с помощью которого по сумме и одному из слагаемых находят другое слагаемое. Число, из которого вычитают называется уменьшаемым, а число, которое вычитают – вычитаемым. Результат вычитания называют разностью.

При вычитании 10-2=8, число 10 – уменьшаемое, 2 – вычитаемое, 8 – разность. При действиях с натуральными числами уменьшаемое не может быть меньше вычитаемого. Разность 2х чисел, показывает, на сколько первое число больше второго, или на сколько второе число меньше первого.

1. Свойство вычитания суммы из числа.

Чтобы вычесть сумму из числа, надо вычесть из числа первое слагаемое, а потом из полученной разности – второе слагаемое.

Например: (6+3)-2=9-2=7

6+(3-2)=6+1=7

(6-2)+3=4+3=2.

2. Свойство вычитания числа из суммы.

Чтобы из суммы вычесть число, надо вычесть его из одного слагаемого, а к полученной разности прибавить другое слагаемое.

Вычитаемое число должно быть меньше слагаемого, из которого его вычитают, или равно ему. Это свойство называют свойством вычитания числа из суммы.

3. Если из числа вычесть нуль, оно не изменится.

Например: 6-0=6

6+0=6.

4. Если из числа вычесть это число, получится нуль.

Например: 6-6=0.

Число, получаемое в результате выполнения всех указанных действий в числовом выражении, называют значением этого выражения. При решении задач записывают действия, а потом их выполняют. Полученные записи называют числовыми выражениями.

Например: 980+(980+50)=2010, 2010 – значение этого выражения.

Выражение, содержащее буквы, называют буквенным выражением. Числа, которыми заменяют букву, называют значениями этой буквы.

Простым называется натуральное число, не имеющее других делителей, кроме 1 и себя самого. Остальные натуральные числа, за исключением 1, называются составными. Натуральное число 1 не является ни простым, ни составным числом. Представление натурального числа n в виде произведения натуральных чисел n=b*с называется разложением на множители.

Для простых чисел – это разложение состоит только из самого числа. Если натуральное число составное, то можно единственным образом представить в виде произведения простых множителей. 19=1*19 При разложении чисел на простые множители используются признаки делимости и применяется запись столбиком, при котором делитель располагается справа от вертикальной черты, а частное записывается под делимым. Так, для числа 360 эта запись будет выглядеть следующим образом:

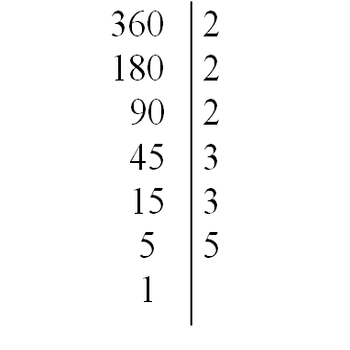
Это и есть основная теорема арифметики.

Из чисел с помощью знаков, арифметических действий и скобок составляют числовые выражения. Если в числовом выражении выполнить указанные действия, соблюдая принятый порядок, то получится число, которое называют значением выражения.

В некоторых случаях, не производя деления натурального числа m на натуральное число n можно ответить на вопрос: выполнимо деление m на n без остатка или нет? Ответ на этот вопрос можно получить с помощью различных признаков делимости:

Теорема 1. Если каждое слагаемое делится на некоторое число, то и сумма делится на это число (теорема о делимости суммы). Не следует, однако, думать, что если каждое слагаемое суммы не делится на какое – то число, то и сумма не делится на это число. Например, сумма 37+19 делится на 4, хотя ни 37, ни 19 не являются кратными числа 4. Заметим, однако, что если все слагаемые, кроме одного, делятся на некоторое число, то сумма не делится на это число.

Теорема 2. Если в произведении один из множителей хотя бы один из множителей делится на некоторое число, то и произведение делится на это число (теорема о делимости произведения). Например, не выполняя умножения, можно утверждать, что произведение 105*48*93*54 делится на 5, так как 105 делится на 5.

Теорема 3. Натуральное число делится на 2 тогда, и только тогда, когда его последняя цифра делится на 2 или равна нулю (признак делимости на 2). Числа, делящие на 2, называются честными и составляют множество честных натуральных чисел.

Теорема 4. Натуральное число делится на 5 тогда, и только тогда, когда его последняя цифра либо 0, либо 5 (признак делимости на 5).

Теорема 5.Натуральное число делится на 19 тогда, и только тогда, когда его последняя цифра 0 (признак делимости на 10).

Теорема 6. Натуральное число, содержащее не менее 3х цифр, делится на 4 двузначное число, образованное последними двумя цифрами заданного числа (признак делимости на 4). Например, число 15436 делится на 4, так как число 36 делится на 4. Число 372506 не делится на 4, так как 06, то есть 6 не делится на 4.

Теорема 7. Натуральное число делится на 3 тогда, и только тогда, когда сумма его цифр делится на 3. Например, число 2742 делится на 3, так как делится на 3 сумм цифр этого числа 2+7+4+2=15. Число 17941 не делится на 3, так как сумма цифр этого числа равна 22, а 22 не делится на 3.

Теорема 8. Натуральное число делится на 9 тогда, когда сумма его цифр делится на 9 (признак делимости на 9).

Глава 3. Занимательные факты о натуральных числах

Кроме ознакомления с теоретическим материалом моей задачей было подобрать занимательные факты из истории натуральных чисел.

^{Число 3}

Число три считалось в древности магическим, потому что оно складывалось из суммы двух предыдущих (3 = 2 + 1), символизировало треугольник, который представляет прошлое, настоящее и будущее. Даже в начале XX века жители некоторых островов Полинезии считали предметы так: один, два, три, много.

Пифагорейцы разбили числа на четные и нечетные. Четные числа считались мужскими, а нечетные – женскими. Одни числа считали счастливыми, а другие –несчастливыми, несущими зло и горе. От Пифагора и его последователей и пошли всякие суеверия, связанные с числами.

Особенно много суеверий связано с числом три.

Те, кто считает его счастливым, говорят: “Бог троицу любит”. Другие напротив, считают его несчастливым. Отсюда и ругательное слово “треклятый”.

Число три играло важную роль в магических обрядах. Все заговоры для придания им большей силы должны были произноситься трижды. От сглаза трижды плюют через левое плечо и трижды стучат по дереву. А троекратный поцелуй по русскому обычаю? В различных поверьях и легендах сохранились триединые действия: скажем, успех

достигался с третьего раза (с третьей попытки). Особенно в спорте. Три попытки попасть в кольцо, полагая, что этого достаточно.

• Легенды тоже не избежали числа три. Например, сказание о том, что Земля

держится на трех китах. Дух триединства проявляет себя везде и во всем. Смотрите сами:

• составляющие времени: прошлое – настоящее – будущее;

• трехмерность пространства: высота – ширина – длина;

• три ветви жизни: животные – растения – микроорганизмы;

• три исторические эпохи: современная – средние века – древний мир;

• три периода жизни человека: молодость – зрелость – старость;

• И, наконец, последний пример: Земля – третья по расстоянию от Солнца

планета Солнечной системы. Да, магическая это цифра – три!

^{Числа 11 и 12}

Наши предки относили к нехорошим числам, число 11. Как теперь установлено, изменения активности Солнца влияют на здоровье людей, а

такие изменения совершаются периодически через каждые 11 лет. Но это совсем не значит, что число 11 имеет мистическое значение.

Очень почиталось число 12, «дюжина». 12 месяцев в году, 12 знаков Зодиака, 12 делений на циферблатах часов, сервизы на 12 персон.

Число 12 замыкало свет, поэтому его считали символом полноты, богатства, счастливым числом. Число 12 имеет собственные делители 2, 3, 4, 6,что при низком уровне вычислений в древности давало большие преимущества.

Вот и закончилось моё исследование на тему «Натуральные числа». Готовя своё исследование, я узнал много нового и интересного о числах, о высказываниях математиков, учёных, живущих в разные века и время.

Эта тема очень обширная и писать можно о числах бесконечно. Чем глубже проникаем в изучение математики, тем больше находим интересных и полезных для себя сведений об этой науке и теме «Натуральные числа».

Математика, скорее всего, никогда не достигла бы такой великой степени совершенства, если бы древние не приложили столько усилий для изучения проблем, которые сегодня воспринимаются нами как истина. Как часто новые методы, новая техника или алгоритм, возникшие при решении, казалось бы, частных задач, приводили науку на новый, более высокий уровень развития!

Без знаний по математики, без знания о натуральных числах, о счёте чисел, мы не смогли бы добиться больших успехов в технике, изобретении, научных открытиях и создании сложных вычислений.

Я буду постоянно следить за литературой о математике, о новых событиях в науке, а также изучать историю математики, работы выдающихся математиков.

1. Большая школьная энциклопедия г. Москва 2004г. «Русское энциклопедическое творчество».

2. Справочник школьника г. Москва 2004г. Авторы: В.А.Гусев и А.Г.Мордкович.

3. Математика – учебник для общеобразовательных учреждений г. Москва 2003г. Авторы: А. Мордкович. Из – во Мнемозина

4. Математика. Г. Москва 1992 г. Авторы: И.В. Степанова, Г.В.Бельтюкова