Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа № 10»
| «Рассмотрено» на школьном методическом совете Протокол № ____от «___» _________ 201 г.
| «Согласовано» Заместитель директора по УВР МБОУ «СОШ № 10» _____ /В.М.Михайлова / «__» __________ 201 г.
| «Утверждаю» Директор МБОУ «СОШ № 10» ______/Т.А Венцкене/ Приказ № ______ от «___» _________ 201 г.
|
РАБОЧАЯ ПРОГРАММА
по алгебре
8 класс
математика
образовательная область
2015-2016 учебный год
Учитель: Зубова Наталья Сергеевна
г. Зима
Пояснительная записка
Рабочая программа по алгебре для 8 класса составлена на основе:
Федерального компонента государственного стандарта (2004 г.);
авторской программы по математике «Алгебра 7-9 классы», И.И.Зубарева, А.Г. Мордкович, издательство «Мнемозина», 2011 год;
учебного плана МБОУ «СОШ№10» на 2015-2016 учебный год, с учетом целей и задач образовательной программы школы и отражает пути реализации содержания учебного предмета.
В настоящей программе реализуется программа развития школы «Развитие культурно-образовательного пространства школы малого города» через включение задач по истории родного города в уроки и факультативные курсы (решение и составление задач, используя различный исторический материал).
Рабочая программа составлена с учетом сформированности мотивационной, интеллектуальной и волевой сфер индивидуальности обучающихся, их образовательных потребностей, индивидуальных особенностей и специфики классных коллективов. В двух 8-х классах обучаются 42 человека. Уровень способностей и мотивации к учению различный. Качество обученности в 8 «а» классе составляет 42 %, тогда как в 8 «б» только 40 %. С учётом этого в содержание уроков включён материал повышенного уровня сложности, предлагаются дифференцированные задания, как на этапе отработки учебного материала, так и на этапе контроля для более подготовленных учащихся, а так же задания по образцу, алгоритму для слабоуспевающих учеников.
В целом восьмиклассники весьма разнородны с точки зрения своих индивидуальных особенностей: памяти, внимания, воображения, мышления, уровня работоспособности, темпа деятельности, темперамента. Это обусловило необходимость использования в работе с ними разных каналов восприятия учебного материала, разнообразных форм и методов работы.
Ведущими методами обучения предмету являются: объяснительно-иллюстративный и репродуктивный, используется и частично-поисковый. На уроках используются элементы технологий личностно-ориентированного обучения, элементы технологий проблемного обучения и деятельностного подхода.
Курс алгебры построен в соответствии с традиционными содержательно-методическими линиями: числовой, функциональной, алгоритмической, уравнений и неравенств, алгебраических преобразований. В 8-м классе продолжается систематизация сведений о преобразовании рациональных выражений и решении уравнений с одним неизвестным. Специальное внимание уделяется новым вопросам: понятиям квадратный корень из числа, квадратное уравнение и неравенство, уравнение с параметром, изучение степени с отрицательным целым показателем. Формируется понятие функции при изучении новых функции и свойства 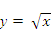 ,
, 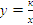 и квадратичной функции. Рассматриваются преобразования графиков функций. Особое внимание уделяется решению квадратных уравнений. Вырабатываются умения применять различные формулы при нахождении корней квадратного уравнения, а также для разложения квадратного трехчлена на множители. Даются первые знания по решению квадратных уравнений с параметром. Серьезное внимание уделяется формированию умений рассуждать, делать простые доказательства, давать обоснования выполняемых действий.
и квадратичной функции. Рассматриваются преобразования графиков функций. Особое внимание уделяется решению квадратных уравнений. Вырабатываются умения применять различные формулы при нахождении корней квадратного уравнения, а также для разложения квадратного трехчлена на множители. Даются первые знания по решению квадратных уравнений с параметром. Серьезное внимание уделяется формированию умений рассуждать, делать простые доказательства, давать обоснования выполняемых действий.
Цели обучения математике в общеобразовательной школе определяются ее ролью в развитии общества в целом и формировании личности каждого отдельного человека. Алгебра нацелена на формирование математического аппарата для решения задач из математики, смежных предметов (физика, химия, основы информатики и вычислительной техники и др.)
Задачи обучения:
овладение системой математических знаний и умений, необходимых для применения практической деятельности изучения смежных дисциплин, продолжения образования;
овладение навыками дедуктивных рассуждений;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, необходимой, в частности, для освоения курса информатики;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и т.д.);
воспитание культуры личности, отношения к математике как части общечеловеческой культуры, понимание значимости математики для научно технического прогресса;
развитие представлений о полной картине мира, о взаимосвязи математики с другими предметами.
Место предмета в учебном плане образовательного учреждения
Согласно учебному плану школы на 2015-2016 учебный год на изучение курса алгебры отводится 102 часа (3 часа в неделю).
Программой предусмотрено проведение:
Контрольная работа №1 по теме: «Алгебраические дроби»
Контрольная работа №2 по теме: «Степень»
Контрольная работа №3 по теме: «Свойства квадратного корня»
Контрольная работа №4по теме: «Квадратичная функция»
Контрольная работа №5 по теме: «Преобразование графика квадратичной функции»
Контрольная работа №6 по теме: «Формулы корней квадратного уравнения»
Контрольная работа №7 по теме: «Квадратные уравнения»
Контрольная работа № 8 по теме: «Неравенства»
Итоговая контрольная работа
Содержание учебного материала
Тема 1. Алгебраические дроби (21 час)
Понятие алгебраической дроби. Основное свойство алгебраической дроби. Сокращение алгебраических дробей. Сложение и вычитание алгебраических дробей. Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень. Рациональное выражение. Рациональное уравнение. Решение рациональных уравнений (первые представления). Степень с отрицательным целым показателем.
Тема 2. Функция 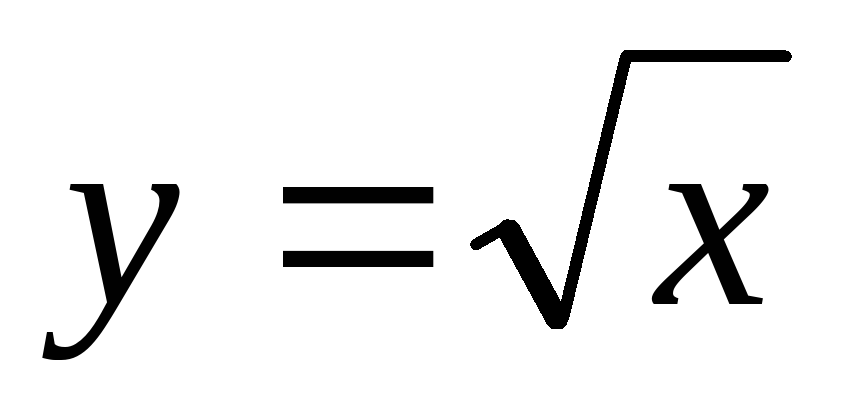 . Свойства квадратного корня (18 часов)
. Свойства квадратного корня (18 часов)
Рациональные числа. Понятие квадратного корня из неотрицательного числа. Иррациональные числа. Множество действительных чисел. Функция 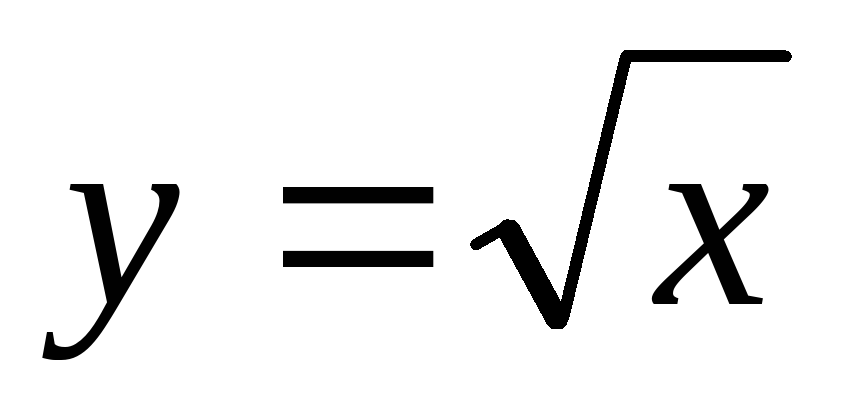 , ее свойства и график. Выпуклость функции. Область значений функции. Свойства квадратных корней. Преобразование выражений, содержащих операцию извлечения квадратного корня. Освобождение от иррациональности в знаменателе. Модуль действительного числа. График функции
, ее свойства и график. Выпуклость функции. Область значений функции. Свойства квадратных корней. Преобразование выражений, содержащих операцию извлечения квадратного корня. Освобождение от иррациональности в знаменателе. Модуль действительного числа. График функции 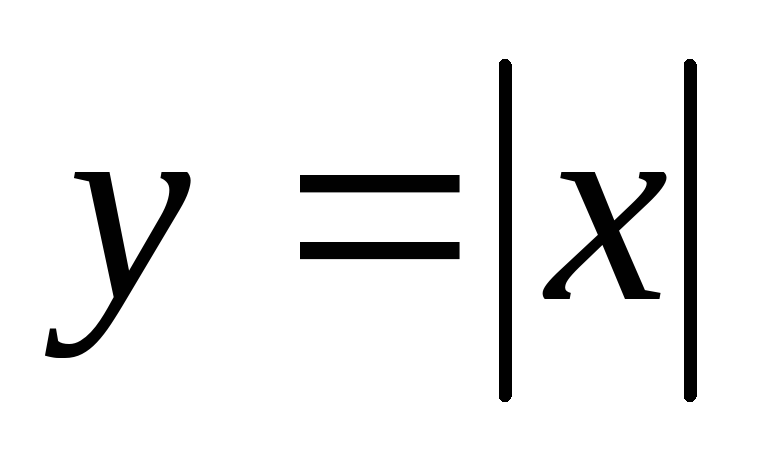 . Формула
. Формула 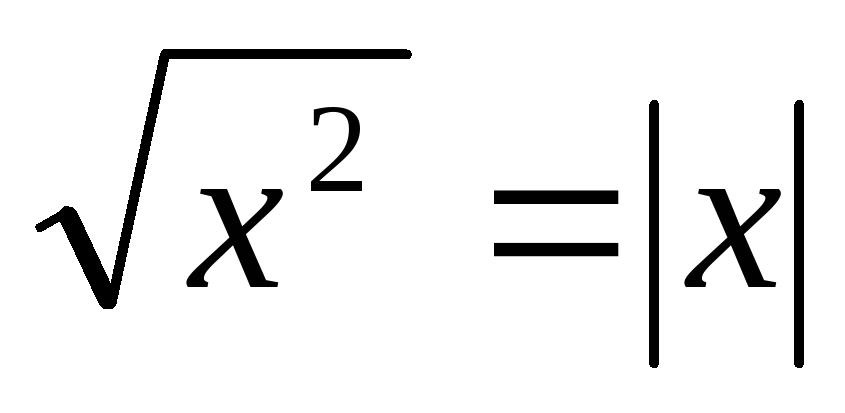 .
.
Тема 3. Квадратичная функция. Функция 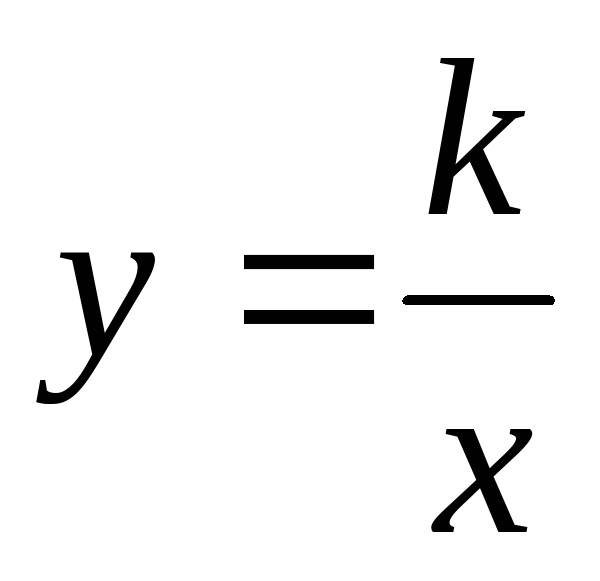 (18 часов).
(18 часов).
Функция  , ее график и свойства. Функция
, ее график и свойства. Функция 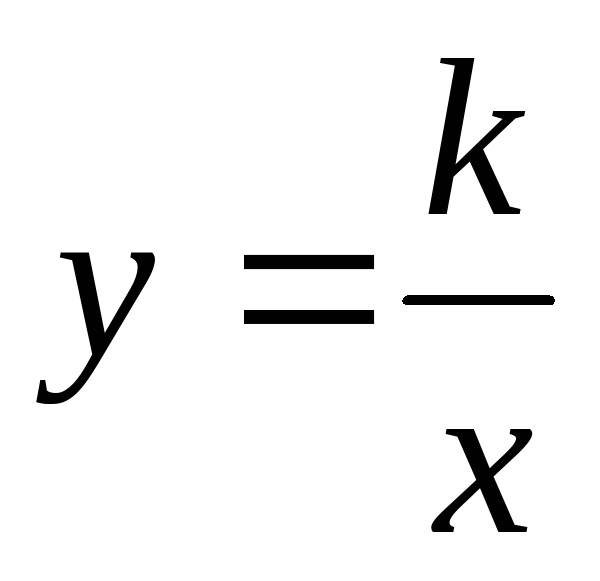 , ее свойства и график. Гипербола. Асимптота. Построение графиков функций у = f(x + l), у = f(x) + т,
, ее свойства и график. Гипербола. Асимптота. Построение графиков функций у = f(x + l), у = f(x) + т,
у = f(x + l) + т, y =- f(x) по известному графику функции y = f(x). Квадратный трехчлен. Квадратичная функция, ее свойства и график. Понятие ограниченной функции. Построение и чтение графиков кусочных функций. Графическое решение квадратных уравнений.
Тема 4. Квадратные уравнения (21 час)
Квадратное уравнение. Приведенное (неприведенное) квадратное уравнение. Полное (неполное) квадратное уравнение. Корень квадратного уравнения. Решение квадратного уравнения методом разложения на множители, методом выделения полного квадрата. Дискриминант. Формулы корней квадратного уравнения. Параметр. Уравнения с параметром (начальные представления). Алгоритм решения рационального уравнения. Биквадратное уравнения. Метод введения новой переменной. Рациональные уравнения как математические модели реальных ситуаций. Частные случаи формулы корней квадратного уравнения. Теорема Виета. Разложение квадратного трехчлена на линейные множители. Иррациональное уравнение. Метод возведения в квадрат. Первые представления о равносильных и неравносильных преобразованиях уравнения. Посторонние корни. Проверка корней.
Тема 5. Неравенства (15 часов)
Свойства числовых неравенств. Неравенство с переменной. Решение неравенств с переменной. Линейное неравенство. Равносильное неравенство. Равносильное преобразование неравенства. Квадратное неравенство. Алгоритм решения квадратного неравенства. Возрастающая функция. Убывающая функция. Исследование функции на монотонность (с использованием свойств числовых неравенств). Приближенные значения действительных чисел, погрешность приближения, приближение по недостатку и избытку. Стандартный вид числа.
Итоговое повторение (9 часов)
Календарно-тематическое планирование
| №№ урока | Дата проведения | Темы |
| план | факт |
| АЛГЕБРАИЧЕСКИЕ ДРОБИ (21 Ч) |
| 01.09. |
| Основные понятия |
| 02.09. |
| Основное свойство алгебраической дроби |
| 04.09. |
| Применение основного свойства дроби |
| 08.09. |
| Правила сложения и вычитания алгебраических дробей с одинаковыми знаменателями |
| 09.09. |
| Сложение и вычитание алгебраических дробей с одинаковыми знаменателями |
| 11.09. |
| Сложение и вычитание алгебраических дробей с разными знаменателями |
| 15.09. |
| Сложение и вычитание алгебраических дробей с разными знаменателями |
| 16.09. |
| Сложение и вычитание алгебраических дробей с разными знаменателями |
| 18.09. |
| Обобщающий урок по теме «Алгебраические дроби» |
| 22.09. |
| Контрольная работа № 1 по теме «Алгебраические дроби» |
| 23.09. |
| Умножение алгебраических дробей. Возведение алгебраической дроби в степень |
| 25.09. |
| Деление алгебраических дробей |
| 29.09. |
| Преобразование рациональных выражений |
| 30.09. |
| Преобразование рациональных выражений |
| 02.10. |
| Преобразование рациональных выражений |
| 06.10. |
| Рациональные уравнения |
| 07.10. |
| Приемы решения рациональных уравнений |
| 09.10. |
| Степень с отрицательным целым показателем |
| 13.10. |
| Действия со степенями |
| 14.10. |
| Обобщающий урок по теме «Степень» |
| 16.10. |
| Контрольная работа № 2 по теме «Степень» |
| ФУНКЦИЯ 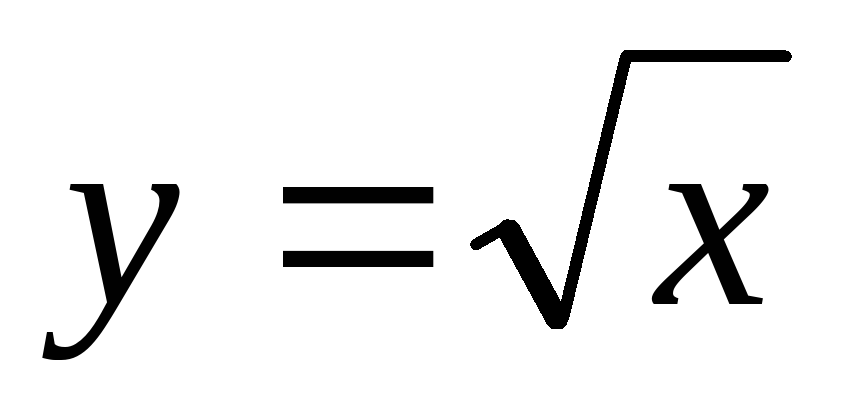 . СВОЙСТВА КВАДРАТНОГО КОРНЯ(18 Ч) . СВОЙСТВА КВАДРАТНОГО КОРНЯ(18 Ч) |
| 20.10. |
| Рациональные числа |
| 21.10. |
| Свойства действий с рациональными числами |
| 23.10. |
| Понятие квадратного корня из неотрицательного числа |
| 27.10. |
| Понятие квадратного корня из неотрицательного числа |
| 28.10. |
| Иррациональные числа |
| 30.10. |
| Множество действительных чисел |
| 10.11. |
| Функция 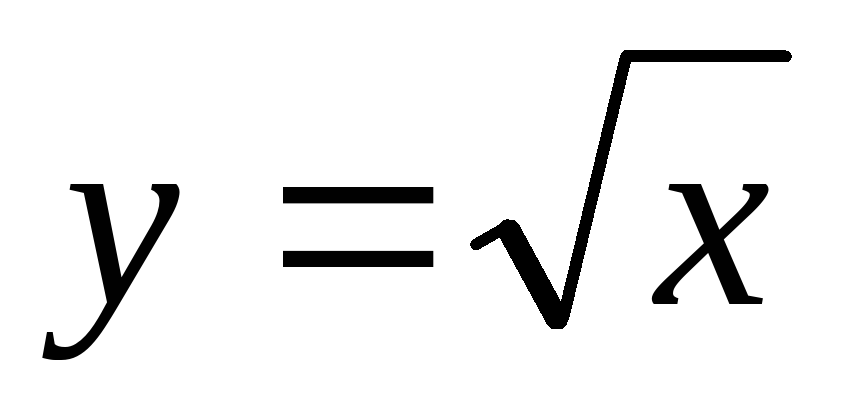 , ее свойства и график , ее свойства и график |
| 11.11. |
| Функция 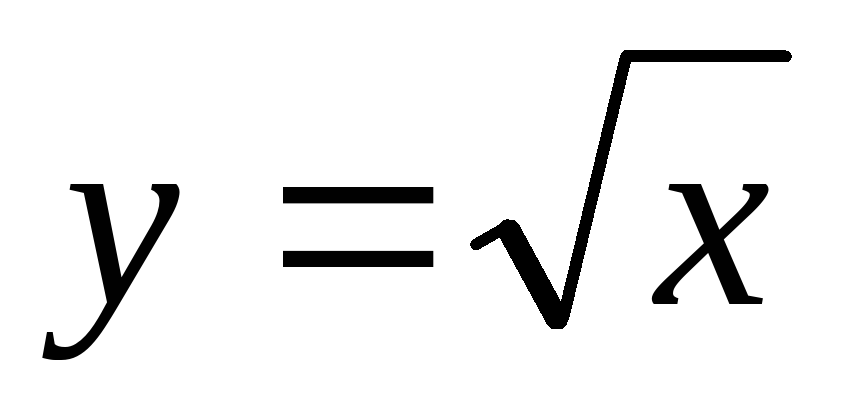 , ее свойства и график , ее свойства и график |
| 13.11. |
| Свойства квадратных корней |
| 17.11. |
| Свойства квадратных корней |
| 18.11. |
| Извлечение квадратного корня |
| 20.11. |
| Преобразование выражений, содержащих операцию извлечения квадратного корня |
| 24.11. |
| Преобразование выражений, содержащих операцию извлечения квадратного корня |
| 25.11. |
| Обобщающий урок по теме «Свойства квадратного корня» |
| 27.11. |
| Контрольная работа № 3 по теме «Свойства квадратного корня» |
| 01.12. |
| Определение модуля |
| 02.12. |
| Модуль действительного числа |
| 04.12. |
| Свойства модуля действительного числа |
| КВАДРАТИЧНАЯ ФУНКЦИЯ. ФУНКЦИЯ 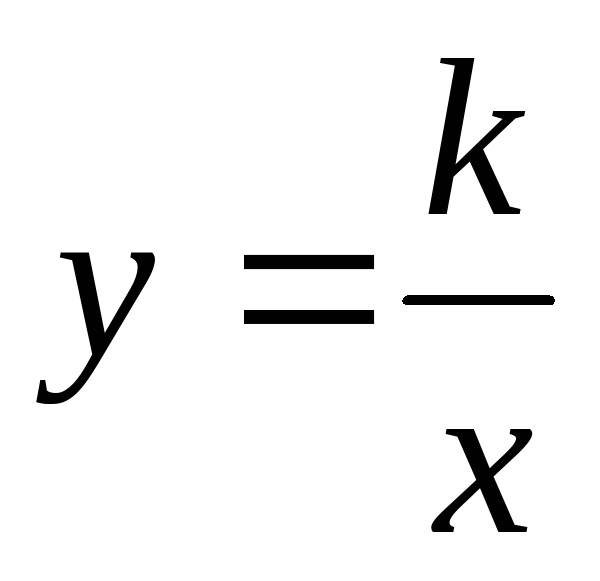 (18 Ч) (18 Ч) |
| 08.12. |
| Функция 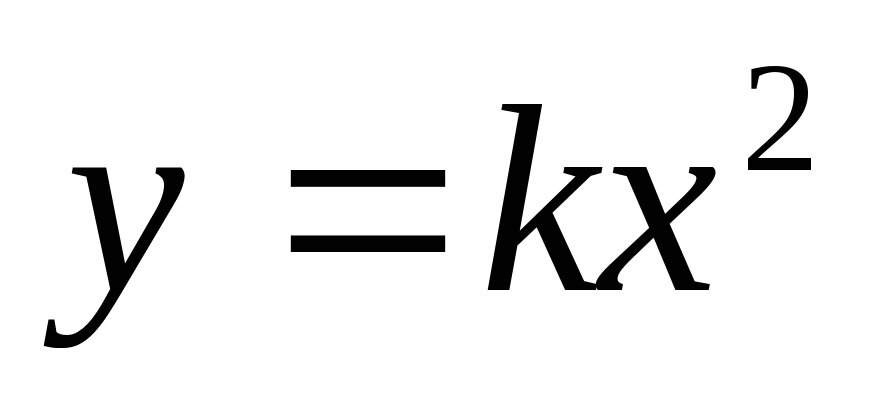 , её свойства и график , её свойства и график |
| 09.12. |
| Функция 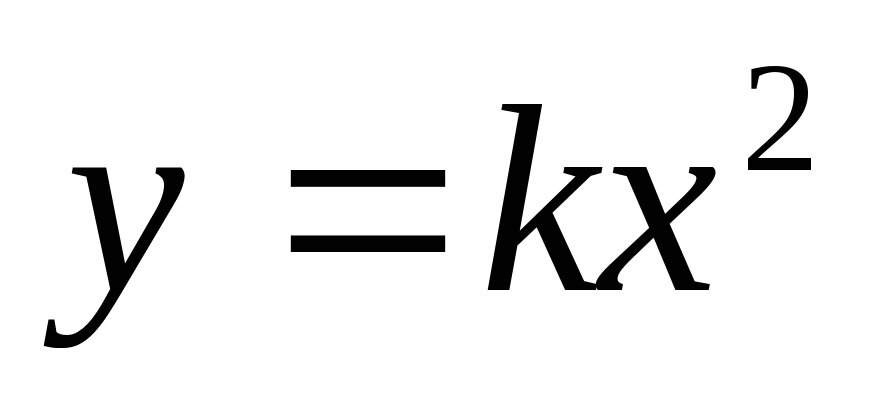 , её свойства и график , её свойства и график |
| 11.12. |
| Функция 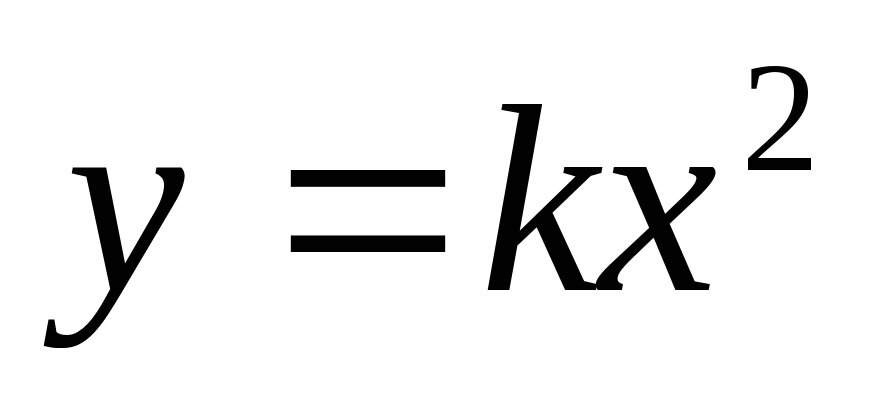 , её свойства и график , её свойства и график |
| 15.12. |
| Функция 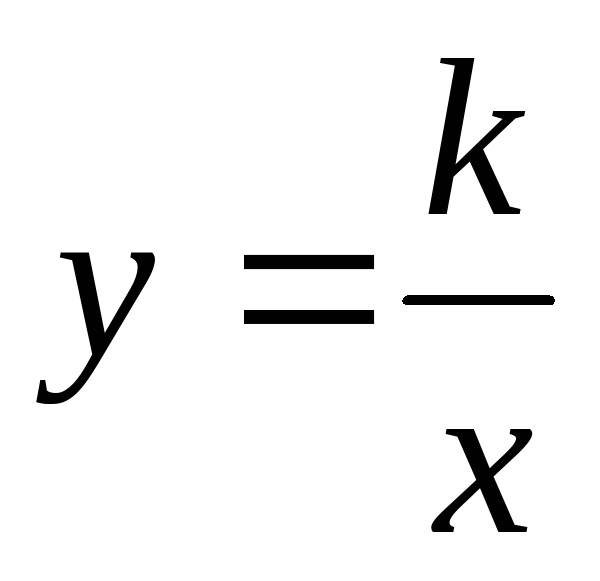 , её свойства и график , её свойства и график |
| 16.12. |
| Функция 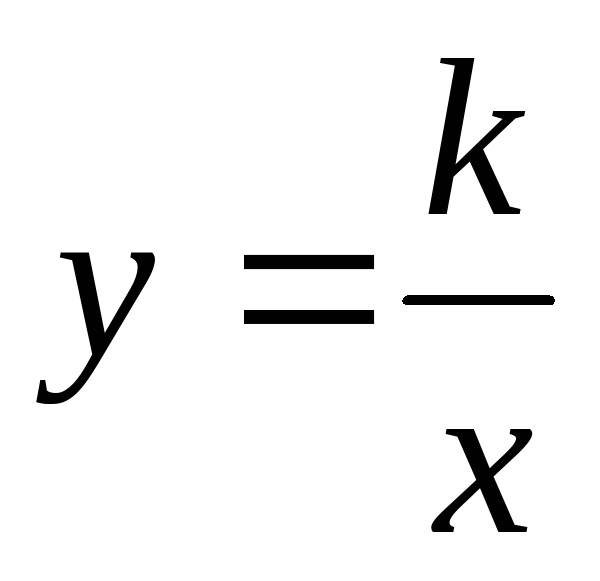 , её свойства и график , её свойства и график |
| 18.12. |
| Контрольная работа № 4 по теме «Квадратичная функция» |
| 22.12. |
| Как построить график функции у = f(x + l), если известен график функции y = f(x) |
| 23.12. |
| Как построить график функции у = f(x + l), если известен график функции y = f(x) |
| 25.12. |
| Как построить график функции у = f(x) + т, если известен график функции y = f(x) |
| 29.12. |
| Как построить график функции у = f(x) + т, если известен график функции y = f(x) |
| 30.12 |
| Как построить график функции у = f(x + l) + m, если известен график функции y = f(x) |
| 12.01. |
| Как построить график функции у = f(x + l) + т, если известен график функции y = f(x) |
| 13.01. |
| Функция у = ах2 + bx + с, ее свойства и график |
| 15.01. |
| Построение графика квадратичной функции |
| 19.01. |
| Построение графика квадратичной функции |
| 20.01 |
| Графическое решение квадратных уравнений |
| 22.01. |
| Обобщающий урок по теме «Преобразование графика квадратичной функции» |
| 26.01. |
| Контрольная работа № 5 по теме «Преобразование графика квадратичной функции» |
| КВАДРАТНЫЕ УРАВНЕНИЯ (21 Ч) |
| 27.01. |
| Основные понятия |
| 29.01. |
| Определение квадратного уравнения и его решений |
| 02.02. |
| Вывод формул корней квадратного уравнения |
| 03.02. |
| Формулы корней квадратного уравнения |
| 05.02. |
| Решение квадратных уравнений с помощью формулы корней |
| 09.02. |
| Рациональные уравнения |
| 10.02. |
| Приемы решения рациональных уравнений |
| 12.02. |
| Обобщающий урок по теме «Формулы корней квадратного уравнения» |
| 16.02. |
| Контрольная работа № 6 по теме «Формулы корней квадратного уравнения» |
| 17.02. |
| Рациональные уравнения как математические модели реальных ситуаций |
| 19.02. |
| Решение текстовых задач с помощью квадратных уравнений |
| 01.03. |
| Решение текстовых задач с помощью квадратных уравнений |
| 02.03. |
| Решение текстовых задач с помощью квадратных уравнений |
| 04.03 |
| Ещё одна формула корней квадратного уравнения |
| 09.03. |
| Ещё одна формула корней квадратного уравнения |
| 11.03. |
| Теорема Виета |
| 15.03. |
| Обобщающий урок по теме «Квадратные уравнения» |
| 16.03. |
| Контрольная работа № 7 по теме «Квадратные уравнения» |
| 18.03. |
| Определение иррационального уравнения и его решений |
| 22.03. |
| Решение иррациональных уравнений |
| 23.03. |
| Решение иррациональных уравнений |
| НЕРАВЕНСТВА (15 Ч) |
| 25.03 |
| Свойства числовых неравенств |
| 29.03. |
| Свойства числовых неравенств |
| 30.03. |
| Свойства числовых неравенств |
| 01.04. |
| Монотонность функций |
| 05.04. |
| Исследование функций на монотонность |
| 06.04. |
| Исследование функций на монотонность |
| 08.04. |
| Линейное неравенство и его решение |
| 19.04. |
| Решение линейных неравенств |
| 20.04. |
| Квадратное неравенство и его решение |
| 22.04. |
| Решение квадратных неравенств |
| 26.04. |
| Решение квадратных неравенств |
| 27.04. |
| Контрольная работа № 8 по теме «Неравенства» |
| 29.04. |
| Приближенные значения действительных чисел |
| 03.05. |
| Погрешность приближения, приближение по недостатку и избытку |
| 04.05. |
| Стандартный вид действительного числа |
| ИТОГОВОЕ ПОВТОРЕНИЕ (9 Ч) |
| 06.05. |
| Преобразование рациональных выражений |
| 10.05. |
| Преобразование рациональных выражений |
| 11.05. |
| Приемы решения квадратных уравнений |
| 13.05. |
| Решение рациональных уравнений |
| 17.05. |
| Итоговая контрольная работа |
| 18.05. |
| Решение текстовых задач с помощью рациональных уравнений |
| 20.05. |
| Решение текстовых задач с помощью рациональных уравнений |
| 24.05. |
| Функции, их свойства и графики |
| 25.05. |
| Преобразование графиков элементарных функций |
Требования к уровню подготовки учащихся 8 классов
В результате изучения курса алгебры 8-го класса учащиеся должны уметь:
систематизировать сведения о рациональных и получить первоначальные представления об иррациональных числах;
бегло и уверенно выполнять арифметические действия с рациональными числами;
вычислять значения числовых выражений, содержащих степени и корни;
научиться рационализировать вычисления;
применять определение и свойства арифметических квадратных корней для вычисления значений числовых выражений и преобразования алгебраических выражений, содержащих квадратные корни;
решать квадратные уравнения и уравнения, сводящиеся к ним, используя приемы и формулы для решения различных видов квадратных уравнений, графический способ решения уравнений;
задачи, сводящиеся к решению квадратных уравнений;
решать линейные неравенства с одной переменной, используя понятие числового промежутка и свойства числовых неравенств, системы линейных неравенств, задачи, сводящиеся к ним;
понимать графическую интерпретацию решения уравнений и систем уравнений, неравенств;
понимать содержательный смысл важнейших свойств функции;
по графику функции отвечать на вопросы, касающиеся её свойств;
строить графики функций – линейной, прямой и обратной пропорциональностей, квадратичной функции и функции у = к/х ;
использовать приобретенные знания, умения, навыки в практической деятельности и повседневной жизни для:
решения несложных практических расчетных задач, в том числе с использованием при необходимости справочной литературы, калькулятора, компьютера;
устной прикидки, и оценки результата вычислений, проверки результата вычислений выполнением обратных действий;
выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;
моделирования практических ситуаций и исследовании построенных моделей с использованием аппарата алгебры;
описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
интерпретации графиков реальных зависимостей между величинами.
Общеучебные умения, навыки и способы деятельности.
В ходе преподавания математики в основной школе, работы над формированием у учащихся перечисленных в программе знаний и умений, следует обращать внимание на то, чтобы они овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:
планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;
решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;
исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;
ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;
проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;
поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.
В результате изучения курса алгебры 8 –го класса учащиеся должны знать:
Понятия:
алгебраическая дробь;
числитель и знаменатель алгебраической дроби;
основное свойство алгебраической дроби;
приведение нескольких алгебраических дробей к общему знаменателю;
рациональное выражение, целое выражение, дробное выражение;
рациональное уравнение;
степень с отрицательным целым показателем;
бесконечная десятичная периодическая дробь (рациональное число);
бесконечная десятичная непериодическая дробь (иррациональное число);
числовая прямая;
квадратный корень из неотрицательного числа;
кубический корень из неотрицательного числа;
подкоренное выражение;
извлечение квадратного (кубического) корня;
освобождение от иррациональности в знаменателе;
модуль;
геометрический смысл модуля;
парабола;
гипербола;
коэффициент обратной пропорциональности;
квадратичная функция;
квадратное уравнение;
квадратный трехчлен;
старший коэффициент, второй коэффициент, свободный член (для квадратного уравнения),
полное квадратное уравнение, неполное квадратное уравнение;
неприведенное и приведенное квадратное уравнение;
корень квадратного уравнения;
дискриминант квадратного уравнения (квадратного трехчлена);
рациональное уравнение;
биквадратное уравнение;
иррациональное уравнение;
параметр, уравнение с параметром;
посторонний корень (для рационального или иррационального уравнения);
равносильные уравнения;
равносильные и неравносильные преобразования уравнения;
линейное неравенство, квадратное неравенство;
решение неравенства;
равносильные неравенства, равносильные преобразования неравенств;
среднее арифметическое, среднее геометрическое двух чисел;
неравенства одинакового смысла, неравенства противоположного смысла;
приближенное значение числа по недостатку, по избытку;
округление чисел;
погрешность (точность) приближения;
стандартный вид положительного числа;
порядок числа.
Формулы и их словесные формулировки:
умножение степеней с одинаковыми основаниями;
деление степеней с одинаковыми основаниями;
возведение степени в степень;
возведение в степень произведение;
возведение в степень дробь;
квадратный корень из произведения;
корень из дроби;
вершины параболы;
корней квадратного уравнения;
разложения квадратного трехчлена на множители;
теорема Виета
свойства числовых неравенств
Свойства функции:
выпуклость функции вверх,
выпуклость функции вниз,
область значений функции,
ограниченность функции снизу,
ограниченность функции сверху.
Алгоритмы:
сложения (вычитания) алгебраических дробей;
отыскания общего знаменателя для нескольких алгебраических дробей;
приведения алгебраических дробей к общему знаменателю;
построения графика функции у = f(x + l) + m;
построения параболы ах2 + bх + с = 0;
решения квадратного уравнения;
решения рационального уравнения;
решения квадратного неравенства.
Правила:
приведение нескольких алгебраических дробей к общему знаменателю;
сложения, вычитания, умножения и деления алгебраических дробей;
возведения алгебраической дроби в натуральную степень;
решения уравнения Р(х) : Q(х) = 0, где Р(х) и Q (х) – многочлены;
преобразования графиков;
решения неравенств с одной переменной;
округления чисел.
Виды контроля результатов обучения
Текущий контроль осуществляется с помощью математических диктантов, самостоятельных и проверочных работ, тестов, блицопросов, тренажеров, устного опроса.
Тематический контроль осуществляется по завершению крупного блока (темы) в форме контрольной работы, тестирования, тренажеров.
Итоговый контроль осуществляется по завершению учебного материала, как оценка результатов обучения за определённый достаточно большой промежуток времени – модуль, полугодие, год.
Методы и формы организации контроля
Устный опрос требует устного изложения учеником изученного материала. Такой опрос может строиться как беседа, рассказ ученика, объяснение, чтение текста, сообщение.
Письменный опрос заключается в проведении различных самостоятельных и контрольных работ.
Тренажеры - электронные и печатные. Они дают возможность тренировать учеников в решении задач и примеров по темам алгебры и обеспечивают эффективную тренировку учеников в устном счете и решении типовых задач. Электронные тренажеры позволяют объективно оценить знания по выбранной теме (оценка выставляется компьютером). Применяю тренажеры как на обычном компьютере при индивидуальном обучении, так и в классе при использовании электронной интерактивной доски.
Тренажеры имеют два режима работы:
1. Режим обучения. Предназначены для использования учеником во время учебного процесса. Он выбирает тему, а тренажер генерирует задание. Каждое последующее задание по теме отличается от предыдущего параметрами, условием и формулировкой вопроса.
2. Режим контроля. В этом режиме формируется группа из нескольких заданий, решение которых позволяет объективно оценить знания по выбранной теме (оценка выставляется компьютером).
Тестирование.
тестовые задания закрытого типа (каждый вопрос сопровождается готовыми вариантами ответов, из которых необходимо выбрать один или несколько правильных);
тестовые задания открытого типа (на каждый вопрос испытуемый должен предложить свой ответ: дописать слово, словосочетание, предложение, знак, формулу и т.д.)
Тестирование проводится с целью диагностики пробелов знаний, контроля уровня обученности учащихся, тренировки технике тестирования. Тесты предлагаются как в печатном, так и в компьютерном варианте. Причем в компьютерном варианте всегда с ограничением времени.
Самостоятельная работа – небольшая по времени (15-20 мин) письменная проверка знаний и умений школьников по небольшой (ещё не пройденной до конца) теме курса. Одной из главных целей этой работы являются проверка усвоения школьниками способов решения учебных задач: осознание понятий, ориентировка в конкретных правилах и закономерностях.
Контрольные работы используются при фронтальном текущем и итоговом контроле с целью проверки знаний и умений школьника по достаточно крупной и полностью изученной теме программы.
Итоговая промежуточная аттестация проходит в форме теста или контрольной работы.
Система контроля складывается из следующих компонентов:
Математические диктанты - форма проверочной работы. Проводится с целью проверки первичного усвоения темы, т.е. обязательный минимум знаний. Обычно на втором уроке после изучения темы. Выставляются только положительные оценки.
Тестирование. Оцениваются выборочные работы.
Самостоятельные работы проводятся с целью проверки закрепления изученной темы. Выставляются только положительные оценки.
Тренажеры - электронные и печатные. Оценка выставляется компьютером за электронные тренажеры, печатные оцениваются все работы.
Контрольные работы составлены по крупным блокам материала или главам учебника. В каждой работе по 5-6 заданий, первые три из них соответствуют уровню обязательной подготовки, последние задания, более продвинутые по уровню сложности. На выполнение контрольной работы отводится 40 минут. Оцениваются все работы.
Система оценки достижений учащихся.
1. Оценка письменных контрольных работ обучающихся по математике.
Ответ оценивается отметкой «5», если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
2.Оценка устных ответов обучающихся по математике
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна – две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке учащихся» в настоящей программе по математике);
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
3. Общая классификация ошибок.
При оценке знаний, умений и навыков учащихся следует учитывать все ошибки (грубые и негрубые) и недочёты.
3.1. Грубыми считаются ошибки:
- незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
- незнание наименований единиц измерения;
- неумение выделить в ответе главное;
- неумение применять знания, алгоритмы для решения задач;
- неумение делать выводы и обобщения;
- неумение читать и строить графики;
- неумение пользоваться первоисточниками, учебником и справочниками;
- потеря корня или сохранение постороннего корня;
- отбрасывание без объяснений одного из них;
- равнозначные им ошибки;
- вычислительные ошибки, если они не являются опиской;
- логические ошибки.
3.2. К негрубым ошибкам следует отнести:
- неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;
- неточность графика;
- нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
- нерациональные методы работы со справочной и другой литературой;
- неумение решать задачи, выполнять задания в общем виде.
3.3. Недочетами являются:
- нерациональные приемы вычислений и преобразований;
- небрежное выполнение записей, чертежей, схем, графиков.
При тестировании все верные ответы берутся за 100%, тогда отметка выставляется в соответствии с таблицей:
| Процент выполнения задания | Отметка |
| 65 % и более | отлично |
| 47-64 %% | хорошо |
| 25-46 %% | удовлетворительно |
| 0-24 %% | неудовлетворительно |
На различных этапах урока применяю компьютер, использую демонстрационный материал и различные мультимедийные продукты как свои, так и готовые.
Литература:
1. А.Г. Мордкович Алгебра – 8.Часть 1. Учебник. Мнемозина, 2008
2. А.Г.Мордкович, Т.Н.Мишустина, Е.Е.Тульчинская, Л.А.Александрова Алгебра-8.
Часть 2. Задачник. Мнемозина, 2008.
3. Л.А.Александрова. Алгебра 8 класс. Контрольные работы. Мнемозина, 2008
4. Л.А.Александрова. Алгебра 8 класс. Самостоятельные работы. Мнемозина, 2008.
12















