СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока

Рабочая программа по алгебре в 8 классе, Алимов
Пояснительная записка
- Цель изучения учебного предмета
Изучение математики в основной школе направлено на достижение следующих целей:
Овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
Развитие таких качеств личности, как ясность и точность мысли, логическое мышление, пространственное воображение, алгоритмическая культура, интуиция, критичность и самокритичность;
Формирование представлений об идеях и методах математики как универсального языка науки и техники, средстве моделирования процессов и явлений;
Воспитание средствами математики культуры личности, знакомство с жизнью и деятельностью видных отечественных и зарубежных ученых – математиков, понимания значимости математики для общественного прогресса.
Просмотр содержимого документа
«Рабочая программа по алгебре в 8 классе, Алимов»
Муниципальное бюджетное образовательное учреждение
«Большеберезниковская средняя общеобразовательная школа »
| Рассмотрено на заседании МО учителей математики Протокол № От« » ------------------ 2014г. Руководитель МО Беськаева Л. И. | Согласовано Зам. директора по УВР
Прокина Н.И.
« » ---------------- 2016г. | Утверждено Директор школы
Кулагин И. А.
« » ----------------- 2016г. |
Рабочая программа
учебного курса алгебра
в 8 «А» классе
3 часа в неделю
Всего 102 часа
Составитель: учитель математики
Устимкина Л. И.
2016-17 учебный год
с. Большие Березники
Пояснительная записка
Цель изучения учебного предмета
Изучение математики в основной школе направлено на достижение следующих целей:
Овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
Развитие таких качеств личности, как ясность и точность мысли, логическое мышление, пространственное воображение, алгоритмическая культура, интуиция, критичность и самокритичность;
Формирование представлений об идеях и методах математики как универсального языка науки и техники, средстве моделирования процессов и явлений;
Воспитание средствами математики культуры личности, знакомство с жизнью и деятельностью видных отечественных и зарубежных ученых – математиков, понимания значимости математики для общественного прогресса.
Общая характеристика учебного предмета
Краткая характеристика
Алгебра формирует математический аппарат для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира. Одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры. Рассматриваемый курс алгебры в 7-9 классах позволяет развивать вычислительные и формально – оперативные алгебраические умения до уровня, позволяющего уверенно использовать их при решении задач математики и смежных предметов (физика, химия, информатика и др.), усваивать аппарат уравнений и неравенств как основное средство математического моделирования прикладных задач, осуществлять функциональную подготовку школьников. Курс характеризуется повышением теоретического уровня обучения, постепенным усилением роли теоретических обобщений и дедуктивных заключений. Прикладная направленность курса обеспечивается систематическим обращением к примерам, раскрывающим возможности применения математики к изучению действительности и решению практических задач.
Указание, на основании которой разработана рабочая программа
Рабочая программа по алгебре разработана на основе: государственных образовательных стандартов по математике, обязательного минимума содержания математического образования; Программы общеобразовательных учреждений. Алгебра. 7 – 9 класса, составитель Т.А.Бурмистрова ..- М.: Просвещение, 2011; методических рекомендаций к разработке календарно-тематического планирования по УМК Алимова Ш.А., Ю.М. Колягин и др. Алгебра. 8 класс. - М.: Просвещение, 2012.
Изменения, внесенные в авторскую программу:
| № п/п | Наименование разделов и тем | Количество часов | |
| По программе | ПТП | ||
| 1 2 3 4 5 6 7 8
| Повторение курса алгебры 7 класса Неравенства Приближенные вычисления Квадратные корни Квадратные уравнения Квадратичная функция Квадратные неравенства Итоговое повторение курса | - 19 14 14 23 16 12 4 | 2 19 10 15 23 16 13 4
|
|
| Итого | 102 | 102 |
|
Общий объем часов на изучение дисциплины, предусмотренный учебным планом. Данная программа разработана в соответствии с учебным планом образовательного учреждения. На изучение предмета алгебра в 8 классе отводится 102 часа. Место учебного предмета в учебном плане среди других учебных дисциплин на определенной ступени образования. На изучение предмета алгебра в 8 классе в инвариантной части школьного учебного плана предусмотрено 102 часа из расчета 3 учебных часа в неделю. | |||
Результаты освоения курса
Требования к уровню подготовки учащихся
Требования к результатам обучения направлены на реализацию деятельностного и личностно ориентированного подходов; освоение учащимися интеллектуальной и практической деятельности; овладение знаниями и умениями, востребованными в повседневной жизни, позволяющими ориентироваться в окружающем мире, значимыми для сохранения окружающей среды и собственного здоровья.
Рубрика «Знать/ понимать» включает требования к учебному материалу, которые усваиваются и воспроизводятся учащимися.
Рубрика «Уметь» включает требования, основанные на более сложных видах деятельности, в том числе творческой: объяснять, изучать, распознавать и описывать, выявлять, сравнивать, определять, анализировать и оценивать, проводить самостоятельный поиск необходимой информации и т.д.
В рубрике «Использовать приобретенные знания и умения в практической деятельности и повседневной жизни» представлены требования, выходящие за рамки учебного процесса и нацеленные на решение разнообразных жизненных задач.
В результате изучения математики ученик должен:
Знать/понимать:
Существо понятия математического доказательства; приводить примеры доказательств;
Существо понятия алгоритма; приводить примеры алгоритмов;
Как используются математические формулы, уравнения и неравенства, примеры их применения для решения математических и практических задач;
Как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
Как потребности практики привели математическую науку к необходимости расширения понятия числа;
Вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов; каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;
Смысл идеализации, позволяющей решать задачи реальной действительности математическими методами и примеры ошибок, возникающих при идеализации.
Арифметика
Уметь:
Выполнять устный счет с целыми числами, обыкновенными и десятичными дробями;
Переходить от одной формы записи чисел к другой, выбирая наиболее подходящую, в зависимости от конкретной ситуации; представлять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной, проценты – в виде дроби и дробь – в виде процентов; применять стандартный вид числа для записи больших и малых чисел; выполнять умножение и деление чисел, записанных в стандартном виде;
Изображать числа точками на координатной прямой;
Выполнять арифметические действия с рациональными числами, сравнивать рациональные числа, находить значения степеней с целыми показателями и корней, находить значения числовых выражений;
Округлять целые числа и десятичные дроби, находить приближенное значение числового выражения;
Пользоваться основными единицами длины, массы, времени, скорости, площади, объема; выражать более крупные единицы через более мелкие и наоборот;
Решать текстовые задачи, включая задачи на движение и работу, задачи, связанные с отношением и с пропорциональностью величин, основные задачи на дроби и на проценты, задачи с целочисленными неизвестными.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни:
Для решения несложных практических расчетных задач, в том числе с использованием, при необходимости. Справочных материалов и простейших вычислительных устройств;
Для устной прикидки и оценки результата вычислений; проверки результата вычисления на правдоподобие, используя различные приемы, интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений.
Алгебра
Уметь:
Составлять буквенные выражения и формулы по условиям задач; осуществлять подстановку одного выражения в другое, осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления; выражать из формул одни переменные через другие;
Выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
Применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
Решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы уравнений;
Решать линейные неравенства с одной переменной и их системы; квадратные неравенства;
Решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, учитывать ограничения целочисленности, диапазона изменения величин;
Определять значения тригонометрических выражений по заданным значениям углов;
Находить значения тригонометрических функций по значению одной из них;
Определять координаты точки в координатной плоскости, строить точки с заданными координатами; решать задачи на координатной плоскости; изображать различные соотношения между двумя переменными, находить координаты точек пересечения графиков;
Применять графические представления при решении уравнений, систем, неравенств;
Находить значения функций, заданных формулой, таблицей, графиком, решать обратную задачу;
Строить графики изученных функций, описывать их свойства, определять свойства функции по ее графику.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни:
Для выполнения расчетов по формулам, понимая формулу как алгоритм вычисления; для составления формул, выражающих зависимости между реальными величинами; для нахождения нужной формулы в справочных материалах;
При моделировании практических ситуаций и исследовании построенных моделей;
При интерпретации графиков зависимостей между величинами; переводя на язык функций и исследуя реальные зависимости;
Для расчетов, включающих простейшие тригонометрические формулы;
При решении планиметрических задач с использованием аппарата тригонометрия.
Элементы логики, комбинаторики, статистики и теории вероятностей
Уметь:
Оценивать логическую правильность рассуждений, в своих доказательствах использовать только логически корректные действия, понимать смысл контрпримеров;
Извлекать информацию, представленную в таблицах, на диаграммах, на графиках, составлять таблицы, строить диаграммы и графики;
Решать комбинаторные задачи путем систематического перебора возможных вариантов и с использованием правила умножения;
Вычислять средние значения результатов измерений;
Находить частоту события;
В простейших случаях находить вероятности случайных событий, в том числе с использованием комбинаторики.
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни:
При записи математических утверждений, доказательств, решении задач;
В анализе реальных числовых данных. Представленных в виде диаграмм, графиков;
При решении учебных и практических задач, осуществляя систематический перебор возможных вариантов;
При сравнении шансов наступления случайных событий;
Для оценки вероятности случайного события в практических ситуациях, сопоставления модели с реальной ситуацией.
Личностные
1) умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
2) критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
3) представление о математической науке как сфере человеческой деятельности, об этапах ее развития, о ее значимости для развития цивилизации;
4) креативность мышления, инициатива, находчивость, активность при решении математических задач;
5) умение контролировать процесс и результат учебной математической деятельности;
6) способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений;
Метапредметные
1) первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;
2) умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
3) умение находить в различных источниках информацию, необходимую для решения математических проблем, и пред-ставлять ее в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
4) умение понимать и использовать математические средства наглядности (графики, диаграммы, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации;
5) умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;
Предметные
1) овладение базовым понятийным аппаратом по основным разделам содержания; представление об основных изучаемых понятиях ( число, геометрическая фигура, уравнение, функция, вероятность) как важнейших математических моделях, позволяющих описывать и изучать реальные процессы и явления;
2) умение работать с математическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики, использовать различные языки математики, проводить классификации, логические обоснования, доказательства математических утверждений;
3) развитие представлений о числе и числовых системах от натуральных до действительных чисел; овладение навыками устных, письменных, инструментальных вычислений;
4) овладение символьным языком алгебры, приемами выполнения тождественных преобразований рациональных выражений, решения уравнений, систем уравнений, неравенств и систем неравенств; умение использовать идею координат на плоскости для интерпретации уравнений, неравенств, систем; умение применять алгебраические преобразования, аппарат уравнений и неравенств для решения задач из различных разделов курса;
5) овладение системой функциональных понятий, функциональным языком и символикой; умение использовать функционально-графические представления для описания и анализа реальных зависимостей;
6) овладение основными способами представления и анализа статистических данных; наличие представлений о статистических закономерностях в реальном мире и о различных способах их изучения, о вероятностных моделях.
7) умение применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использованием при необходимости справочных мат-лов, калькулятора, компьютера.
Тематическое планирование по дисциплине «Алгебра »
| № п/п | Наименование разделов и тем | Максимальная нагрузка учащего. ч | Из них | ||||
| Теоретическое обучение, ч | Лабораторные и практические работы, ч | Контрольные работы, ч | Экскурсии, ч | Самостоятельные работы, | |||
| 1 | Повторение курса алгебры 7 класса | 2 |
|
|
|
|
|
| 2 | Неравенства | 19 | 16 |
| 1 |
| 2 |
| 3 | Приближенные вычисления | 10 | 9 |
|
|
| 1 |
| 4 | Квадратные корни | 15 | 13 |
| 1 |
| 1 |
| 5 | Квадратные уравнения | 23 | 21 |
| 1 |
| 1 |
| 6 | Квадратичная функция | 16 | 14 |
| 1 |
| 1 |
| 7 | Квадратные неравенства | 13 | 11 |
| 1 |
| 1 |
| 8 | Итоговое повторение курса | 4 | 3 |
| 1 |
|
|
|
| Итого | 102 | 89 |
| 6 |
| 7 |
|
| |||||||
Содержание тем учебного курса
1. Повторение курса алгебры 7 класса (2 ч).
2. Неравенства (19 ч).
Положительные и отрицательные числа. Числовые неравенства. Основные свойства числовых неравенств. Сложение и умножение неравенств. Строгие и нестрогие неравенства. Неравенства с одним неизвестным. Решение неравенств. Системы неравенств с одним неизвестным. Числовые промежутки. Решение систем неравенств. Модуль числа. уравнения и неравенства, содержащие модуль.
Самостоятельная работа по теме «Решение неравенств».
Самостоятельная работа по теме «Решение систем неравенств».
После изучения темы учащиеся должны:
Знать: определение положительного и отрицательного чисел; определение рационального числа; свойства чисел; определение большего числа; основные свойства числовых неравенств; теоремы о сложении и умножении неравенств; понятие строгого и не строгого неравенства; определение решения неравенства; алгоритм решения неравенств; определение решения систем неравенств; определение числовых промежутков; алгоритм решения систем неравенств; определение модуля числа; правило решения уравнений с модулем; правило решения неравенств с модулем;
Уметь: формулировать свойства числовых неравенств, обосновывать их опираясь на координатную прямую; применять свойства неравенств в ходе решения задач. Решать линейные неравенства, системы линейных неравенств. Изображать на координатной прямой множество решений неравенств. Выполнять вычисления, доказывать неравенства, решать уравнения используя свойства числовых неравенств; сравнивать числовые неравенства, доказывать неравенства; применять основные свойства неравенств; доказывать неравенства с применением свойств; доказывать и решать неравенства с применением теорем об умножении и сложении; решать линейные неравенства и показывать на числовой прямой множество их решений; решать системы неравенств; записывать результаты с помощью числовых промежутков; решать простейшие уравнения и неравенства содержащие модуль.
3. Приближенные вычисления(10 часов).
Приближенные значения величин. Погрешность приближения. Оценка погрешности. Округление чисел. Относительная погрешность. Простейшие вычисления на микрокалькуляторе. Стандартный вид числа. Вычисления на микрокалькуляторе степени числа, обратного данному. Последовательное выполнение операций на микрокалькуляторе. Вычисления на микрокалькуляторе с использованием ячейки памяти.
Самостоятельная работа по теме «Стандартный вид числа».
После изучения темы учащиеся должны:
Знать: определение абсолютной погрешности приближения; правило нахождения оценки погрешности; правило округления чисел; определение относительной погрешности; запись числа в стандартном виде; правило сложения и вычитания, умножения и деления приближенных значений; Определение степени с натуральным показателем;
Уметь: находить, анализировать, сопоставлять числовые характеристики объектов окружающего мира; использовать запись числа в стандартном виде для выражения размеров объектов, длительности процессов в окружающем мире; сравнивать числа и величины, записанные с использованием степени 10; использовать разные формы записи приближенных значений; округлять натуральные числа и десятичные дроби; выполнять прикидку и оценку результатов вычислений. Находить абсолютную погрешность приближения; находить приближенное значение с недостатком и с избытком; давать оценку абсолютной погрешности; округлять числа; находить относительную погрешность; записывать числа в стандартном виде; выполнять задания с применением правил сложения, вычитания, умножения и деления приближенных значений
4. Квадратные корни (15 часов).
Арифметический квадратный корень. Действительные числа. Квадратный корень из степени. Квадратный корень из произведения. Квадратный корень из дроби.
Самостоятельная работа по теме «Квадратный корень из дроби и произведения».
После изучения темы учащиеся должны:
Знать: определение арифметического квадратного корня; алгоритм преобразования обыкновенной дроби в десятичную, алгоритм преобразования бесконечной периодической дроби в обыкновенную; квадратный корень из степени; квадратный корень из произведения; квадратный корень из дроби;
Уметь: доказывать свойства арифметических квадратных корней; применять их к преобразованию выражений; вычислять значения выражений, содержащих квадратные корни; Вычислять арифметический квадратный корень из чисел; записывать обыкновенные дроби в виде конечной или бесконечной периодической десятичной дроби; записывать бесконечные периодические десятичные дроби в виде обыкновенных; применять теоремы о корне из степени, произведения, дроби при выполнении вычислений
5. Квадратные уравнения (23 часа).
Квадратное уравнение и его корни. Неполные квадратные уравнения. Метод выделения полного квадрата. Решение квадратных уравнений. Приведенное квадратное уравнение. Теорема Виета. Уравнения, сводящиеся к квадратным. Решение задач с помощью квадратных уравнений. Решение простейших систем, содержащих уравнение второй степени.
Самостоятельная работа по теме «Решение квадратных уравнений».
После изучения темы учащиеся должны:
Знать: определение квадратного уравнения; теорему о корнях квадратного уравнения;
Виды неполных квадратных уравнений; метод выделения полного квадрата; формулу корней квадратного уравнения общего вида; алгоритм решения квадратных уравнений; определение приведенного квадратного уравнения; формулу корней приведенного квадратного уравнения; теорему Виета и ей обратную; теорему о разложении квадратного трехчлена на множители; определение биквадратного уравнения; Приемы решения простейших систем, содержащих уравнения второй степени;
Уметь: распознавать квадратные уравнения; решать квадратные уравнения, а так же уравнения сводящиеся к ним; решать дробно-рациональные уравнения; определять наличие корней квадратного уравнения по дискриминанту и коэффициентам; решать текстовые задачи алгебраическим способом: переходить от словесной формулировки условия задачи к алгебраической модели путем составления уравнения; решать составленное уравнение; интерпретировать результат. Находить квадратные уравнения; находить корни простейшего квадратного уравнения; решать неполные квадратные уравнения; выделять полный квадрат; решать квадратные уравнения методом выделения полного квадрата; решать квадратные уравнения с помощью формулы корней квадратного уравнения общего вида; решать приведенные квадратные уравнения с использованием формулы корней и теоремы обратной теореме Виета; раскладывать квадратный трехчлен на множители; решать биквадратное уравнение; решать уравнения содержащие неизвестное в знаменателе; Решать задачи с помощью квадратного уравнения; решать простейшие системы, содержащие уравнения второй степени;
6. Квадратичная функция (16 часов).
Определение квадратичной функции. Функция у =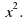 Функция у =
Функция у = 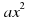 . Функция у =
. Функция у = 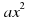 + вх + с. Построение графика квадратичной функции.
+ вх + с. Построение графика квадратичной функции.
Самостоятельная работа по теме «Построение графика квадратичной функции».
После изучения темы учащиеся должны:
Знать: определение квадратичной функции; свойства функции у=х2; у=ах2; у=ах2+bх+с; Что такое функция; Способы задания функции; Как построить график линейной функции.
Уметь: вычислять значение функций заданных формулами; строить по точкам графики функции; описывать свойства функции на основе ее графического представления; строить графики квадратичных функций и описывать их свойства по графику. Распознавать квадратичную функцию; Находить нули функции; строить графики квадратичной функции; описывать свойства квадратичной функции
7. Квадратные неравенства (13 часов).
Квадратное неравенства и его решение. Решение квадратного неравенства с помощью графика квадратичной функции. Метод интервалов. Исследование квадратного трехчлена.
Самостоятельная работа по теме «Метод интервалов»
После изучения темы учащиеся должны:
Знать: определение квадратного неравенства; алгоритм решения неравенства с помощью графика; метод интервалов; теоремы о зависимости дискриминанта и квадратичной функции.
Уметь: распознавать квадратные неравенства; решать квадратные неравенства; решать квадратные неравенства использую графические представления. Решать квадратное неравенство путем перехода к системе неравенств; решать неравенство с помощью графика; решать неравенства методом интервалов; исследовать квадратичную функцию.
|
|
Обобщение и систематизация знаний. Повторение основных понятий и типичных задач. Проверить знания учащихся и выяснить степень усвоения ими материала 8 класса.
|
|
Календарно – тематическое планирование
Количество часов в неделю -3
Всего 102
| № п/п | Наименование разделов и тем | Вид занятия | Количество часов | Вид самостоятельной работы | Дата проведения занятий | |
| планируемая | фактическая | |||||
| 1 | Повторение курса алгебры 7 класса | Обобщение и систематизация знаний | 2 |
|
|
|
| 2 | Неравенства |
| 19 |
|
|
|
| 2.1 | Положительные и отрицательные числа | Введение в тему | 1 |
|
|
|
| Закрепление изученного материала | 1 |
|
|
| ||
| 2.2 | Числовые неравенства | Введение в тему | 1 |
|
|
|
| 2.3 | Основные свойства числовых неравенств | Введение в тему | 1 |
|
|
|
| Закрепление изученного материала | 1 |
|
|
| ||
| 2.4 | Сложение и умножение неравенств | Введение в тему | 1 |
|
|
|
| 2.5 | Строгие и нестрогие неравенства | Введение в тему | 1 |
|
|
|
| 2.6 | Неравенства с одним неизвестным | Введение в тему | 1 |
|
|
|
| 2.7 | Решение неравенств | Введение в тему | 1 |
|
|
|
| Закрепление изученного материала | 1 |
|
|
| ||
|
|
| Применение знаний и умений | 1 | Тест |
|
|
| 2.8 | Системы неравенств с одним неизвестным. Числовые промежутки | Введение в тему | 1 |
|
|
|
| 2.9 | Решение систем неравенств | Введение в тему | 1 |
|
|
|
| Закрепление изученного материала | 1 |
|
|
| ||
| Применение знаний и умений | 1 | Тест |
|
| ||
| 2.10 | Модуль числа. уравнения и неравенства, содержащие модуль | Введение в тему | 1 |
|
|
|
| Закрепление изученного материала | 1 |
|
|
| ||
| 2.11 | Обобщающий урок | Обобщение и систематизация знаний | 1 |
|
|
|
| 2.12 | Контрольная работа №1 по теме «Неравенства» | Контроль знаний и умений | 1 |
|
|
|
| 3 | Приближенные вычисления |
| 10 |
|
|
|
| 3.1 | Приближенные значения величин. Погрешность приближения | Введение в тему | 1 |
|
|
|
| 3.2 | Оценка погрешности | Введение в тему | 1 |
|
|
|
| 3.3 | Округление чисел | Введение в тему | 1 |
|
|
|
| 3.4 | Относительная погрешность | Введение в тему | 1 |
|
|
|
| 3.5 | Простейшие вычисления на микрокалькуляторе | Введение в тему | 1 |
|
|
|
| 3.6 | Стандартный вид числа | Введение в тему Применение знаний и умений | 1 1 |
Самостоятельная работа |
|
|
| 3.7 | Вычисления на микрокалькуляторе степени числа, обратного данному | Применение знаний и умений | 1 |
|
|
|
| 3.8 | Последовательное выполнение операций на микрокалькуляторе | Применение знаний и умений | 1 |
|
|
|
| 3.9 | Вычисления на микрокалькуляторе с использованием ячейки памяти | Применение знаний и умений | 1 |
|
|
|
| 4 | Квадратные корни |
| 15 |
|
|
|
| 4.1 | Арифметический квадратный корень | Введение в тему | 1 |
|
|
|
| Закрепление изученного материала | 1 |
|
|
| ||
| 4.2 | Действительные числа | Введение в тему | 1 |
|
|
|
| Закрепление изученного материала | 1 |
|
|
| ||
| 4.3 | Квадратный корень из степени | Введение в тему | 1 |
|
|
|
| Закрепление изученного материала | 1 |
|
|
| ||
| Применение знаний и умений | 1 |
|
|
| ||
| 4.4 | Квадратный корень из произведения | Введение в тему | 1 |
|
|
|
| Закрепление изученного материала | 1 |
|
|
| ||
| Применение знаний и умений | 1 |
|
|
| ||
| 4.5 | Квадратный корень из дроби | Введение в тему | 1 |
|
|
|
| Закрепление изученного материала | 1 |
|
|
| ||
| Применение знаний и умений | 1 |
Проверочная работа |
|
| ||
| 4.6 | Обобщающий урок | Обобщение и систематизация знаний | 1 |
|
|
|
| 4.7 | Контрольная работа №2 по теме «Квадратные корни» | Контроль знаний и умений | 1 |
|
|
|
| 5 | Квадратные уравнения |
| 23 |
|
|
|
| 5.1 | Квадратное уравнение и его корни | Введение в тему | 1 |
|
|
|
| Закрепление изученного материала | 1 |
|
|
| ||
| 5.2 | Неполные квадратные уравнения | Введение в тему | 1 |
|
|
|
| 5.3 | Метод выделения полного квадрата | Введение в тему | 1 |
|
|
|
| 5.4
| Решение квадратных уравнений | Введение в тему | 1 |
|
|
|
| Закрепление изученного материала | 1 |
|
|
| ||
| Применение знаний и умений | 1 |
|
|
| ||
| Применение знаний и умений | 1 | Проверочная работа |
|
| ||
| 5.5 | Приведенное квадратное уравнение. Теорема Виета | Введение в тему Закрепление изученного материала | 1 1 |
|
|
|
| Применение знаний и умений | 1 |
|
|
| ||
| 5.6 | Уравнения, сводящиеся к квадратным | Введение в тему | 1 |
|
|
|
| Закрепление изученного материала | 1 |
|
|
| ||
| Применение знаний и умений | 1 |
|
|
| ||
| 5.7 | Решение задач с помощью квадратных уравнений | Введение в тему | 1 |
|
|
|
| Закрепление изученного материала Применение знаний и умений | 1 |
|
|
| ||
| Применение знаний и умений | 1 |
|
|
| ||
| Расширение и углубление знаний по теме | 1 |
|
|
| ||
| 5.8 | Решение простейших систем, содержащих уравнение второй степени | Введение в тему | 1 |
|
|
|
| Закрепление изученного материала | 1 |
|
|
| ||
| Применение знаний и умений | 1 |
|
|
| ||
| 5.9 | Обобщающий урок | Обобщение и систематизация знаний | 1 |
|
|
|
| 5.10 | Контрольная работа №3 по теме «Квадратные уравнения» | Контроль знаний и умений | 1 |
|
|
|
| 6 | Квадратичная функция |
| 16 |
|
|
|
| 6.1 | Определение квадратичной функции | Введение в тему | 1 |
|
|
|
| 6.2 | Функция у = | Введение в тему | 1 |
|
|
|
| 6.3 | Функция у = | Введение в тему | 1 |
|
|
|
| Закрепление изученного материала | 1 |
|
|
| ||
| Применение знаний и умений | 1 |
|
|
| ||
| 6.4 | Функция у = | Введение в тему | 1 |
|
|
|
| Закрепление изученного материала | 1 |
|
|
| ||
| Применение знаний и умений | 1 |
|
|
| ||
| 6.5 | Построение графика квадратичной функции | Введение в тему | 1 |
|
|
|
| Закрепление изученного материала | 1 |
|
|
| ||
| Применение знаний и умений | 1 |
|
|
| ||
| Расширение и углубление знаний по теме | 1 |
|
|
| ||
| Расширение и углубление знаний по теме | 1 | Проверочная работа |
|
| ||
| Расширение и углубление знаний по теме | 1 |
|
|
| ||
| 6.6 | Обобщающий урок | Обобщение и систематизация знаний | 1 |
|
|
|
| 6.7 | Контрольная работа №4 по теме «Квадратичная функция» | Контроль знаний и умений | 1 |
|
|
|
| 7 | Квадратные неравенства |
| 13 |
|
|
|
| 7.1 | Квадратное неравенства и его решение | Введение в тему | 1 |
|
|
|
| Закрепление изученного материала | 1 |
|
|
| ||
| 7.2 | Решение квадратного неравенства с помощью графика квадратичной функции | Введение в тему | 1 |
|
|
|
| Закрепление изученного материала | 1 |
|
|
| ||
| Применение знаний и умений Применение знаний и умений | 1 |
|
|
| ||
| Расширение и углубление знаний по теме | 1 |
|
|
| ||
| Расширение и углубление знаний по теме | 1 |
|
|
| ||
| 7.3 | Метод интервалов | Введение в тему Закрепление изученного материала | 1 1 |
|
|
|
| Применение знаний и умений | 1 | Тест |
|
| ||
| 7.4 | Исследование квадратного трехчлена | Введение в тему | 1 |
|
|
|
| 7.5 | Обобщающий урок | Обобщение и систематизация знаний | 1 |
|
|
|
| 7.6 | Контрольная работа №5 по теме «Квадратные неравенства» | Контроль знаний и умений | 1 |
|
|
|
| 8 | Итоговое повторение курса | Обобщение и систематизация знаний | 4 |
|
|
|
| 8.1 | Итоговая контрольная работа №6 | Контроль знаний и умений | 1 |
|
|
|
|
| Итого |
| 102 | 7 |
|
|
Контроль уровня обученности
(Контрольно-измерительный материал)
Контрольная работа №1 по теме «Неравенства»
Контрольная работа №2 по теме «Квадратные корни»
Контрольная работа №3 по теме «Квадратные уравнения»
Контрольная работа №1 по теме «Квадратичная функция»
Контрольная работа №5 по теме «Квадратные неравенства»
Итоговая контрольная работа №6
Материально – техническое обеспечение
Перечень оборудования
| № п/п | Перечень оборудования (имеющего в наличии) | Примечание |
|
| Библиотечный фонд (книгопечатная продукция) |
|
| 1 2
3 4 5 6
| Стандарт среднего общего образования по предмету математика Примерная программа общеобразовательного учреждения. Математика, 5-11 классы Учебники по математике, алгебре, геометрии, рекомендованные Министерством образования и науки РФ Учебные пособия по математике Энциклопедии по математике, справочные пособия Методические пособия по математике |
|
|
| Информационно-коммуникационные средства |
Входит в материально-техническое обеспечение образовательного учреждения |
| 8 | Мультимедийные обучающие программы и учебники | |
|
| Технические средства обучения (ТСО) | |
| 9 10 11 12 13 14 15 | Мультимедийный компьютер Аудиторная доска с магнитной поверхностью и набором приспособлений для крепления таблиц Экран (навесной) Мультимедийный проектор Сканер Копировальный аппарат
|
Учебно – методическое обеспечение
Учебно – программные материалы
1.Программы общеобразовательных учреждений: Алгебра , 7 – 9 классы, составитель Т. А. Бурмистрова. Москва, «Просвещение»,2010.
2. Программно - методические материалы. Математика, 5 – 11 классы. Москва, 2004.
3. Сборник нормативных документов. Математика. Федеральный компонент государственного стандарта. Федеральный базисный план. Москва, «Дрофа», 2006.
Учебно – теоретические материалы
1. Алгебра: Учебник для 8 класса общеобразовательных учреждений / Ш. А. Алимов, Ю М. Колягин, Ю. В. Сидоров и др. – М.: «Просвещение», 2011.
2.Изучение алгебры в 7 -9 классах: кН. Для учителя Ю. М. Колягин, Ю. В. Сидоров, М. В. Ткачева и др. - М.: Просвещение, 2008.
3. Ткачева М. В. Элементы статистики и вероятность: учебн. пособие для 7 – 9 кл./ М. В. Ткачева, Н. Е. Федорова. – М.: Просвещение, 2008.
Учебно – практические материалы
1.Звавич Л. И., Кузнецова Л. В., Суворова С. Б. Дидактические материалы по алгебре для 8 класса. - М.: «Просвещение», 2011.
2.Контрольно – измерительные материалы. Алгебра: 8 класс/ Сост. В. В. Черноруцкий. – М.: ВАКО, 2011.
3. Ткачева М. В.Сборник задач по алгебре для 7 – 9 классов / М. В. Ткачева, Р. Г. Газарян. - М.: Просвещение, 2008.
Муниципальное бюджетное образовательное учреждение
«Большеберезниковская средняя общеобразовательная школа »
| Рассмотрено на заседании МО учителей математики Протокол № От« » ------------------ 2016г. Руководитель МО Беськаева Л. И. | Согласовано Зам. директора по УВР
Прокина Н.И.
« » ---------------- 2016г. | Утверждено Директор школы
Кулагин И. А.
« » ----------------- 2016г. |
Рабочая программа
учебного курса геометрия
в 8 «А» классе
2 часа в неделю, всего 68 часов
Составитель: учитель математики
Устимкина Л. И.
2016-17 учебный год
с. Большие Березники
Пояснительная записка
Цель изучения учебного предмета
Изучение геометрии в основной школе направлено на достижение следующих целей:
Овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
Развитие таких качеств личности, как ясность и точность мысли, логическое мышление, пространственное воображение, алгоритмическая культура, интуиция, критичность и самокритичность;
Формирование представлений об идеях и методах математики как универсального языка науки и техники, средстве моделирования процессов и явлений;
Воспитание средствами математики культуры личности, знакомство с жизнью и деятельностью видных отечественных и зарубежных ученых – математиков, понимания значимости математики для общественного прогресса.
Общая характеристика учебного предмета
Краткая характеристика
Геометрия – один из важнейших компонентов математического образования, необходимый для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания учащихся, Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства. Рассматриваемый курс геометрии в 7-9 классах характеризуется рациональным сочетанием логической строгости и геометрической наглядности. Увеличивается теоретическая значимость изучаемого материала, расширяются внутренние логические связи курса, повышается роль дедукции, степень абстрактности изучаемого материала. Учащиеся овладевают приемами аналитико – синтетической деятельности при доказательстве теорем и решении задач. Систематическое изложение курса позволяет начать работу по формированию представлений учащихся о строении математической теории, обеспечивает развитие логического мышления школьников. Изложение материала характеризуется постоянным обращением к наглядности, использованием рисунков и чертежей на всех этапах обучения и развитием геометрической интуиции на этой основе. Целенаправленное обращение к примерам из практики развивает умения учащихся вычленять геометрические факты, формы и отношения в предметах и явлениях действительности, использовать язык геометрии для их описания.
-Указание, на основании которой разработана рабочая программа
Рабочая программа составлена на основе:
федерального компонента государственного стандарта общего образования,
федерального перечня учебников, рекомендованных Министерством образования Российской Федерации к использованию в образовательном процессе в общеобразовательных учреждениях на 2016-2017 учебный год,
на основе программы для общеобразовательных учреждений. Геометрия , 7 – 9 классы. Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др., 2009г, в соответствии с федеральным компонентом государственного образовательного стандарта по предмету математика, примерной программой среднего (полного) общего образования, федеральным базисным планом.
Изменения, внесенные в авторскую программу:
1 час из итогового повторения добавлен на вводное повторение. Поэтому на вводное повторение отводится 1 час, а на итоговое повторение –3 часа.
Общий объем часов на изучение дисциплины, предусмотренный учебным планом.
Данная программа разработана в соответствии с учебным планом образовательного учреждения. На изучение предмета геометрия в 8 классе отводится 68 часов.
Место учебного предмета в учебном плане, среди других учебных дисциплин на определенной ступени образования.
На изучение предмета геометрия в 8 классе в инвариантной части школьного учебного плана предусмотрено 68 часов из расчета 2 учебных часа в неделю.
Результаты освоения курса
Требования к уровню подготовки учащихся
Требования к результатам обучения направлены на реализацию деятельностного и личностно ориентированного подходов; освоение учащимися интеллектуальной и практической деятельности; овладение знаниями и умениями, востребованными в повседневной жизни, позволяющими ориентироваться в окружающем мире, значимыми для сохранения окружающей среды и собственного здоровья.
Рубрика «Знать/ понимать» включает требования к учебному материалу, которые усваиваются и воспроизводятся учащимися.
Рубрика «Уметь» включает требования, основанные на более сложных видах деятельности, в том числе творческой: объяснять, изучать, распознавать и описывать, выявлять, сравнивать, определять, анализировать и оценивать, проводить самостоятельный поиск необходимой информации и т.д.
В рубрике «Использовать приобретенные знания и умения в практической деятельности и повседневной жизни» представлены требования, выходящие за рамки учебного процесса и нацеленные на решение разнообразных жизненных задач.
В результате изучения математики ученик должен:
Знать/понимать:
Существо понятия математического доказательства; приводить примеры доказательств;
Существо понятия алгоритма; приводить примеры алгоритмов;
Как используются математические формулы, уравнения и неравенства, примеры их применения для решения математических и практических задач;
Как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
Как потребности практики привели математическую науку к необходимости расширения понятия числа;
Вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
Каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;
Смысл идеализации, позволяющей решать задачи реальной действительности математическими методами и примеры ошибок, возникающих при идеализации.
Уметь:
Пользоваться геометрическим языком для описания предметов окружающего мира;
Распознавать геометрические фигуры, различать их взаимное расположение;
Изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразования фигур;
Распознавать на чертежах, моделях и в окружающей обстановке основные пространственные тела, изображать их;
В простейших случаях строить сечения и развертки пространственных тел;
Проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами;
Вычислять значения геометрических величин ( длин, углов, площадей, объемов); в том числе: для углов от 0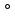 до 180
до 180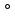 определять значения тригонометрических функций по заданным значениям углов; находить значения тригонометрических функций по значению одной из них, находить стороны, углы и площади треугольников, длины ломаных, дуг окружности, площадей основных геометрических фигур и фигур, составленных из них;
определять значения тригонометрических функций по заданным значениям углов; находить значения тригонометрических функций по значению одной из них, находить стороны, углы и площади треугольников, длины ломаных, дуг окружности, площадей основных геометрических фигур и фигур, составленных из них;
Решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, соображения симметрии;
Проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;
Решать простейшие планиметрические задачи в пространстве;
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни:
Описания реальных ситуаций на языке геометрии;
Расчетов, включающих простейшие тригонометрические формулы;
Решения геометрических задач с использованием тригонометрии;
Решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);
Построений геометрическими инструментами (линейка, угольник, циркуль, транспортир).
Результаты освоения курса
Личностные
1) умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
2) критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
3) представление о математической науке как сфере человеческой деятельности, об этапах ее развития, о ее значимости для развития цивилизации;
4) креативность мышления, инициатива, находчивость, активность при решении математических задач;
5) умение контролировать процесс и результат учебной математической деятельности;
6) способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений;
Метапредметные
1) первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;
2) умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
3) умение находить в различных источниках информацию, необходимую для решения математических проблем, и пред-ставлять ее в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
4) умение понимать и использовать математические средства наглядности (графики, диаграммы, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации;
5) умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;
Предметные
1) овладение базовым понятийным аппаратом по основным разделам содержания; представление об основных изучаемых понятиях ( число, геометрическая фигура, уравнение, функция, вероятность) как важнейших математических моделях, позволяющих описывать и изучать реальные процессы и явления;
2) умение работать с математическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики, использовать различные языки математики, проводить классификации, логические обоснования, доказательства математических утверждений;
3) развитие представлений о числе и числовых системах от натуральных до действительных чисел; овладение навыками устных, письменных, инструментальных вычислений;
4) овладение символьным языком алгебры, приемами выполнения тождественных преобразований рациональных выражений, решения уравнений, систем уравнений, неравенств и систем неравенств; умение использовать идею координат на плоскости для интерпретации уравнений, неравенств, систем; умение применять алгебраические преобразования, аппарат уравнений и неравенств для решения задач из различных разделов курса;
5) овладение системой функциональных понятий, функциональным языком и символикой; умение использовать функционально-графические представления для описания и анализа реальных зависимостей;
6) овладение основными способами представления и анализа статистических данных; наличие представлений о статистических закономерностях в реальном мире и о различных способах их изучения, о вероятностных моделях.
7) умение применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использованием при необходимости справочных мат-лов, калькулятора, компьютера.
Тематическое планирование по дисциплине «Геометрия»
| № | Наименование разделов и тем | Максималь ная нагрузка учащегося, ч | Из них | ||||
| Теоретическое обучение, ч | Лабораторные и практи ческие работы, ч | Контрольные работы, ч | Самостоя тельные работы, ч | Экскур сии, ч | |||
| 1 | Вводное повторение
| 1 | 1 |
|
|
|
|
| 2 | Четырехугольники
| 14 | 11 |
| 1 | 2 |
|
| 3 | Площадь | 14 | 11 |
| 1 | 2 |
|
| 4 | Подобные треугольники | 19 | 15 |
| 2 | 2 |
|
| 5 | Окружность
| 17 | 14 |
| 1 | 2 |
|
| 6 | Итоговое повторение | 3 | 2 |
| 1 |
|
|
|
| Итого | 68 | 54 |
| 6 | 8 |
|
Cодержание учебного предмета
1. Вводное повторение (1 час)
2. Четырехугольники( 14 часов)
Многоугольники. Параллелограмм и трапеция. Прямоугольник, ромб, квадрат.
Самостоятельная работа по теме «Параллелограмм, трапеция».
Самостоятельная работа по теме «Прямоугольник, ромб, квадрат».
После изучения темы учащиеся должны:
Знать: определение многоугольника и четырёхугольника и их элементов; понятие выпуклого многоугольника; утверждение о сумме углов выпуклого многоугольника; определение и признаки параллелограмма, свойство противолежащих углов и сторон параллелограмма, свойство диагоналей параллелограмма, определение трапеции, равнобокой и прямоугольной трапеции; определение треугольника, ромба и квадрата как частных видов параллелограмма, определение фигур, обладающих центральной и осевой симметрией; понимать, какие точки симметричны относительно оси и точки.
Уметь: изображать многоугольники и четырёхугольники, называть по рисунку их элементы: диагонали, вершины, стороны, соседние и противоположные вершины и стороны, применять полученные знания в ходе решения задач; воспроизводить доказательства признаков и свойств параллелограмма и трапеции и применять их при решении задач; применять свойства прямоугольника, ромба и квадрата при решении задач, изображать, обозначать и распознавать на рисунке точки, симметричные данным относительно прямой и точки, решать простейшие задачи на применение понятий центральной и осевой симметрии.
3.Площадь(14 часов)
Площадь многоугольника. Площади параллелограмма, треугольника и трапеции. Теорема Пифагора.
Самостоятельная работа по теме «Площадь параллелограмма и трапеции».
Самостоятельная работа по теме «Теорема Пифагора».
После изучения темы учащиеся должны:
Знать: основные свойства площади, формулу площади прямоугольника; формулы для вычисления площади параллелограмма, треугольника, трапеции; формулировки теоремы Пифагора и теоремы, обратной теореме Пифагора.
Уметь: выводить формулу площади прямоугольника, применять полученные знания в ходе решения задач; проводить доказательства справедливости полученных формул, воспроизводить доказательства теоремы Пифагора; применять доказанные теоремы в решении задач применять их для решения задач.
4. Подобные треугольники (19 часов).
Определение подобных треугольников. Признаки подобия треугольников. Применение подобия к доказательству теорем и решению задач. Соотношение между сторонами и углами треугольника.
Самостоятельная работа по теме «Применение подобия к доказательству теорем и решению задач».
Самостоятельная работа по теме «Соотношение между сторонами и углами треугольника».
После изучения темы учащиеся должны:
Знать: определение пропорциональных отрезков и подобных треугольников, коэффициента подобия, формулировку теоремы об отношении площадей подобных треугольников; формулировки и доказательства признаков подобия треугольников; определение средней линии треугольника, формулировка теоремы о средней линии треугольника, пропорциональные отрезки в прямоугольном треугольнике; определение синуса, косинуса и тангенса острого угла прямоугольного треугольника, основное тригонометрическое тождество, значения синуса, косинуса и тангенса углов 300, 450 и 600.
Уметь: доказывать теорему об отношении площадей подобных треугольников, применять полученные сведения в решении простейших задач; применять признаки подобия треугольников для решения задач; воспроизводить доказательство теоремы о средней линии треугольника и применять её при решении задач, решать задачи на построение методом подобия; вычислять значения синуса, косинуса и тангенса острого угла прямоугольного треугольника при решении конкретных задач, строить угол по значению его синуса, косинуса и тангенса, решать задачи на вычисление элементов прямоугольного треугольника .
5. Окружность (17 часов).
Касательная к окружности. Центральные и вписанные углы. Четыре замечательные точки треугольника. Вписанные и описанные окружности.
Самостоятельная работа по теме «Центральные и вписанные углы»
Самостоятельная работа по теме «Вписанные и описанные окружности»
После изучения темы учащиеся должны:
Знать: определение секущей и касательной к окружности, свойство касательной и признак касательной, случаи взаимного расположения прямой и окружности; что такое центральный угол, градусная мера дуги окружности, определение угла, вписанного в окружность, формулировки теорем о точках пересечения биссектрис, высот и медиан треугольника, а также серединных перпендикуляров к сторонам треугольника; определение окружности, вписанной в многоугольник, и окружности, описанной около многоугольник; определение многоугольника, вписанного в окружность и многоугольника, описанного около окружности, формулировки теорем об окружности, вписанной в треугольник, и окружности, описанной около треугольника, формулировки свойств и признаков вписанных и описанных четырёхугольников; формулировка теоремы о вписанных углах и её следствия .
Уметь: доказывать свойство касательной и признак касательной, применять полученные сведения при решении задач; изображать и распознавать центральный угол и дугу окружности, изображать и распознавать центральный угол и дугу окружности, соответствующую данному центральному углу, вписанный угол, - применять полученные знания при решении задач; воспроизводить доказательство изученных теорем, применять изученные теоремы в процессе решения задач; доказывать теоремы об окружности, вписанной в треугольник, и окружности, описанной около треугольника, использовать изученные понятия и теоремы в решении задач.
6.Итоговое повторение (3 часа).
Календарно-тематическое планирование
| № п/п | Наименование разделов и тем | Вид занятия | Количество часов | Вид самостоятельной работы | Дата проведения | ||
| планируемая | фактическая | ||||||
| 1 | Вводное повторение |
| 1 |
|
|
| |
| 2 | Четырехугольники |
| 14 |
|
|
| |
| 2.1 | Многоугольники | Введение в тему | 1 |
|
|
| |
|
|
| Применение знаний и умений | 1 |
|
|
| |
| 2.2 | Параллелограмм и трапеция | Введение в тему | 1 |
|
|
| |
|
|
| Комбинированное | 1 |
|
|
| |
|
|
| Комбинированное | 1 |
|
|
| |
|
|
| Применение знаний и умений | 1 |
|
|
| |
|
|
| Применение знаний и умений Практикум | 1
1 | Тест |
|
| |
| 2.3
| Прямоугольник, ромб, квадрат | Введение в тему Комбинированное | 1
1 |
|
|
| |
|
|
| Комбинированное | 1 |
|
|
| |
|
|
| Применение знаний и умений | 1 | Тест
|
|
| |
| 2.4 | Решение задач | Практикум | 1 |
|
|
| |
| 2.5 | Контрольная работа № 1 по теме: «Четырёхугольники» | Контроль знаний и умений | 1 |
|
|
| |
| 3 | Площадь |
| 14 |
|
|
| |
| 3.1 | Площадь многоугольника | Введение в тему | 1 |
|
|
| |
|
|
| Применение знаний и умений | 1 |
|
|
| |
| 3.2 | Площади параллелограмма, треугольника и трапеции | Введение в тему
| 1 |
|
|
| |
|
|
| Комбинированное | 1 |
|
|
| |
|
|
| Комбинированное | 1 |
|
|
| |
|
|
| Применение знаний и умений | 1 |
|
|
| |
|
|
| Практикум
| 1 | Тест
|
|
| |
|
|
| Практикум
| 1 |
|
|
| |
| 3.3 | Теорема Пифагора | Введение в тему | 1 |
|
|
| |
|
|
| Применение знаний и умений
| 1 |
|
|
| |
|
|
| Практикум | 1 | Самостоятельная работа
|
|
| |
| 3.4 | Решение задач | Практику | 1 |
|
|
| |
|
|
| Практикум | 1 |
|
|
| |
| 3.5 |
Подобные треугольники | Контроль знаний и умений | 1 | | | | |
| 4 | | 19 | | | | ||
| 4.1 | Определение подобных треугольников | Введение в тему | 1 | | | | |
| | | Применение знаний и умений | 1 | | | | |
| 4.2 | Признаки подобия треугольников. | Введение в тему | 1 | | | | |
| | | Применение знаний и умений | 1 | | | | |
| | | Комбинированное | 1 | | | | |
| | | Применение знаний и умений | 1 | | | | |
| | | Практикум | 1 | | | | |
| 4.3 | Контрольная работа № 3 по теме: «Подобные треугольники» | Контроль знаний и умений | 1 | | | | |
| 4.4 | Применение подобия к доказательству теорем и решению задач | Введение в тему | 1 | | | | |
| | | Комбинированное | 1 | | | | |
| | | Комбинированное | 1 | Тест | | | |
| | | Применение знаний и умений | 1 | | | | |
| | | Применение знаний и умений | 1 | | | | |
| | | Практикум | 1 | | | | |
| | | Практикум | 1 | | | | |
| 4.5 | Соотношение между сторонами и углами треугольника | Введение в тему | 1 | | | | |
| | | Применение знаний и умений | 1 | Самостоятельная работа | | | |
| | | Практикум | 1 | | | | |
| 4.6 | Контрольная работа № 4 по теме: «Применение подобия к решению задач» | Контроль знаний и умений | 1 | | | | |
| 5 | Окружность | | 17 | | | | |
| 5.1 | Касательная к окружности | Введение в тему | 1 | | | | |
| | | Применение знаний и умений | 1 | | | | |
| | | Практикум | 1 | | | | |
| 5.2 | Центральные и вписанные углы | Введение в тему | 1 | | | | |
| | | Комбинированное | 1 | | | | |
| | | Применение знаний и умений | 1 | Тест | | | |
| | | Практикум | 1 | | | | |
| 5.3 | Четыре замечательные точки треугольника | Введение в тему | 1 | | | | |
| | | Комбинированное | 1 | | | | |
| | | Комбинированное | 1 | | | | |
| 5.4 | Вписанные и описанные окружности | Введение в тему | 1 | | | | |
| | | Комбинированное | 1 | | | | |
| | | Комбинированное | 1 | Тест | | | |
| | | Применение знаний и умений | 1 | | | | |
| 5.5 | Решение задач | Практикум | 1 | | | | |
| | | Практикум | 1 | | | | |
| 5.6 | Контрольная работа № 5 по теме: «Окружность» | Контроль знаний и умений | 1 | | | | |
| 6 | Итоговое повторение | Обобщение и систематиза ция знаний | 3 | | | | |
| 6.1 | Итоговая контрольная работа №6 | Контроль знаний и умений | 1 | | | | |
| | Итого | | 68 | 8 | | | |
Контроль уровня обученности
(Контрольно-измерительный материал)
Контрольная работа № 1 по теме: «Четырёхугольники»
Контрольная работа № 2 по теме: «Площади»
Контрольная работа № 3 по теме: «Подобные треугольники»
Контрольная работа № 4 по теме: «Применение подобия к решению задач»
Контрольная работа № 5 по теме: «Окружность»
Итоговая контрольная работа №6
Материально – техническое обеспечение
Перечень оборудования
| № п/п | Перечень оборудования (имеющего в наличии) | Примечание |
|
| Библиотечный фонд (книгопечатная продукция) |
|
| 1
2
3
4 | Стандарт среднего общего образования по предмету математика Примерная программа общеобразовательного учреждения. Математика, 5-11 классы Учебники по математике, алгебре, геометрии, рекомендованные Министерством образования и науки РФ Учебные пособия по математике Энциклопедии по математике, справочные пособия Методические пособия по математике |
|
| 5 | Информационно-коммуникационные средства | Входит в материально-техническое обеспечение образовательного учреждения |
| 6 | Мультимедийные обучающие программы и учебники | |
| 7 8 | Технические средства обучения (ТСО) | |
| 9 10 11 12 13 14 15 | Мультимедийный компьютер Аудиторная доска с магнитной поверхностью и набором приспособлений для крепления таблиц Экран (навесной) Мультимедийный проектор Сканер Копировальный аппарат |
Учебно – методическое обеспечение
Учебно – программные материалы
1.Программы общеобразовательных учреждений:Геометрия, 7 – 9 классы, составитель Т. А. Бурмистрова. Москва, «Просвещение»,2010.
2.Программно - методические материалы. Математика, 5 – 11 классы. Москва, 2004.
3. Сборник нормативных документов. Математика. Федеральный компонент государственного стандарта. Федеральный базисный план. Москва, «Дрофа», 2006
Учебно – теоретические материалы
1. Геометрия: Учебник для 7 - 9 классов общеобразовательных учреждений / Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др. – М.: «Просвещение», 2008.
2.Изучение геометрии в 7 -9 классах: кн. для учителя / Л. С. Атанасян, В. Ф. Бутузов, Ю. А. Глазков, И. И. Юдина и др. - М.: Просвещение, 2008.
Учебно – практические материалы
1.Зив Б. Г. Дидактические материалы по геометрии для 8 класса. - М.: «Просвещение», 2008.
2.Контрольно – измерительные материалы. геометрия: 8 класс/ Сост. Н. Ф. Гаврилова. – М.: ВАКО, 2011.