Рабочая программа учебного курса по математике для 8 класса.
Пояснительная записка
Рабочая программа составлена в соответствии с:
Федеральным компонентом государственного образовательного стандарта начального общего, основного общего и среднего (полного) общего образования (Приказ МО РФ от 05.03.2004 №1089).
Примерной программой основного общего образования по математике.
Федеральным базисным учебным планом для среднего (полного) общего образования (Приложение к приказу Минобразования России от 09.03.2004 № 1312).
Методическими рекомендациями авторов учебников: «Алгебра 8» А. Г. Мордковича.; «Геометрия 7-9» И. М. Смирнова, В. А. Смирнов.
Срок реализации данной программы 1 год.
В течение года возможны коррективы рабочей программы, связанные с объективными причинами.
Согласно Федеральному базисному учебному плану данная рабочая программа предусматривает обучение в объеме 170 часов (5 часов в неделю). Из них: Алгебра – 102 часа, Геометрия – 68 часов.
Промежуточная аттестация проводится в форме тестов, самостоятельных, проверочных работ и математических диктантов (по 10 - 15 минут) в конце логически законченных блоков учебного материала. Итоговая аттестация предусмотрена в виде административной контрольной работы.
Самостоятельные, тестовые и контрольные работы используемые при обучении взяты из дидактического материала составленного к УМК. Самостоятельных работ - 56, контрольных работ – 15 , тестов – 13.
Цели обучения математике:
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.
Реализация календарно-тематического плана обеспечивает освоение общеучебных умений и компетенций в рамках информационно-коммуникативной деятельности:
создание условия для умения логически обосновывать суждения, выдвигать гипотезы и понимать необходимость их проверки, ясно, точно и грамотно выражать свои мысли в устной и письменной речи;
формирование умения использовать различные языки математики, свободно переходить с языка на язык для иллюстрации, интерпретации, аргументации и доказательства, интегрирования в личный опыт новой, в том числе самостоятельно полученной информации;
создание условия для плодотворного участия в работе в группе, самостоятельной и мотивированной организации своей деятельности, использования приобретенных знаний и навыков в практической деятельности и повседневной жизни для исследования (моделирования) несложных практических ситуаций на основе изученных формул.
Педагогические технологии используемые на уроках
| № | Название технологии | Результат использования |
| 1 | Развивающее обучение | Всестороннее гармоничное развитие личности |
| 2 | Проблемное обучение | Разработка новых подходов к объяснению нового материала |
| 3 | Разноуровневое обучение | Разработка разноуровневых заданий, формирование практико-лабораторной базы |
| 4 | Технология блочно-модульного обучения | Усиление здоровьесберегающего аспекта предметного обучения, разработка мониторинга |
| 5 | Лекционно - зачётная система | Повышение качества обученности на базе на базе отработки образовательных стандартов |
| 6 | Технология игрового обучения | Усиление здоровьесберегающего аспекта предметного обучения |
| 7 | Технология перспективно - опережающего обучения | Развитие навыков публичного обучения |
| 8 | Информационно – коммуникативные технологии | Использование обучающего программирования развития навыков работы с компьютером, в Интернете |
| 9 | Обучение в сотрудничестве | Развитие взаимоответственных способов обучения при поддержке одноклассников |
| 10 | Технология уровневой дифференциации | Отработка образовательных стандартов |
| 11 | Проектные методы обучения | Выход проектов за рамки предметного обучения |
Условные обозначения
Типы уроков:
УОНМ — урок ознакомления с новым материалом.
УЗИМ — урок закрепления изученного материала.
УПЗУ — урок применения знаний и умений.
УОСЗ — урок обобщения и систематизации знаний.
УПКЗУ — урок проверки и коррекции знаний и умений
. КУ – комбинированный урок
Виды контроля:
С – самостоятельная работа
Т – тест
Содержание тем учебного курса математики для 8 класса
Алгебра
Алгебраические дроби (21 ч)
Понятие алгебраической дроби. Основное свойство алгебраической дроби. Сокращение алгебраических дробей.
Сложение и вычитание алгебраических дробей.
Умножение и деление алгебраических дробей. Возведение алгебраической дроби в степень.
Рациональное выражение. Рациональное уравнение. Решение рациональных уравнений (первые представления).
Степень с отрицательным целым показателем.
Цель изучения:
– формирование представлений о многочлене от одной переменной, алгебраической дроби, о рациональном выражении;
– формирование умений деления многочлена на многочлен с остатком, разложения многочлена на множители, сокращения дробей, приведения алгебраических дробей к общему знаменателю;
– овладение умением упрощения выражений, сложения и вычитания, умножения и деления алгебраических дробей с разными знаменателями;
– овладение навыками преобразования рациональных выражений, доказательства тождеств, решения рациональных уравнений способом освобождения от знаменателей с составлением математической модели реальной ситуации.
Функция у = х. Свойства квадратного корня (18 ч)
Рациональные числа. Понятие квадратного корня из неотрицательного числа. Иррациональные числа. Множество действительных чисел.
Функция у = х, её свойства и график. Выпуклость функции. Область значений функции.
Свойства квадратных корней. Преобразование выражений, содержащих операцию извлечения квадратного корня. Освобождение от иррациональности в знаменателе дроби. Модуль действительного числа. График функции у = х. Формула х2 =х.
Цель изучения:
– формирование представлений о квадратном корне из неотрицательного числа, о функции у = х;
– формирование умений построения графика функции у = х и описания ее свойств, использования алгоритма извлечения квадратного корня;
– овладение умением преобразовывать выражения, содержащие операцию извлечения квадратного корня, применяя свойства квадратных корней;
– овладение навыками решения уравнений, содержащих радикал.
– овладение умением построения графика функции модуль, описания ее свойств;
– формирование представлений о рациональных, иррациональных и действительных числах, модуле действительного числа, о делимости чисел, признаках делимости, необходимом и достаточном условии делимости чисел, о НОД и НОК нескольких натуральных чисел;
– формирование умений применять основную теорему арифметики, находить каноническое разложение на простые множители.
Квадратичная функция. Функция у = к/х (18 ч)
Функция у = ах2, её график и свойства.
Функция у = к/х, её свойства и график. Гипербола. Асимптота.
Построение графиков функций у = (х + l), y = (х) + m, у = (х + l) + m, y = -(х) по известному графику функции y = (х).
Квадратный трёхчлен. Квадратичная функция, её свойства и график. Понятие ограниченной функции. Построение и чтение графиков кусочных функций, составленных из функций у = С, у = kx + m, y = k/x, y = ax2 + bx + c, y = х, y = х.
Графическое решение квадратных уравнений.
Цель изучения:
– формирование представлений о функции y = kx2, функции у = k/x, гиперболе, перемещении графика по координатной плоскости, квадратичной функции y = ax2 + bx + c;
– формирование умений построения графиков функций y = kx2, у = k/x, y = ax2 + bx + c и описание их свойств;
– овладение умением использования алгоритма построения графика функции y = f(x + l) + m, y = f(x + l), y = f(x) + m;
– овладение навыками решения квадратных уравнений графическим способом, построения дробно-линейной функции.
Квадратные уравнения (21 ч)
Квадратное уравнение. Приведённое (неприведённое) квадратное уравнение. Полное (неполное) квадратное уравнение. Корень квадратного уравнения. Решение квадратного уравнения методом разложения на множители, методом выделения полного квадрата.
Дискриминант. Формулы корней квадратного уравнения. Параметр. Уравнение с параметром (начальные сведения).
Алгоритм решения рационального уравнения. Биквадратное уравнение. Метод введения новой переменной.
Рациональные уравнения как математические модели реальных ситуаций.
Частные случаи формулы корней квадратного уравнения.
Теорема Виета. Разложение квадратного трёхчлена на линейные множители.
Иррациональное уравнение. Метод возведения в квадрат. Первые представления о равносильных и неравносильных преобразованиях уравнения. Посторонние корни. Проверка корней.
Цель изучения:
– формирование представлений о полном, приведенном, неполном квадратном уравнении, дискриминанте квадратного уравнения, формулах корней квадратного уравнения, теореме Виета;
– формирование умений решить приведенное квадратное уравнение, применяя обратную теорему Виета;
– овладение умением разложения квадратного трехчлена на множители, решения квадратного уравнения по формулам корней квадратного уравнения;
– овладение навыками решения рационального и иррационального уравнения как математической модели реальных ситуаций.
Неравенства (15 ч)
Свойства числовых неравенств.
Неравенство с переменной. Решение неравенств с переменной. Линейно неравенство. Равносильные неравенства. Равносильное преобразование неравенства.
Квадратное неравенство. Алгоритм решения квадратного неравенства.
Исследование функций на монотонность ( с использованием свойств числовых неравенств).
Приближённые значения действительных чисел, погрешность приближения, приближение по недостатку и избытку. Стандартный вид числа.
Цель изучения:
– формирование представлений о числовых неравенствах, неравенстве с одной переменной
о среднем арифметическом и среднем геометрическом, о неравенстве Коши;
– формирование умений исследования функции на монотонность, применения приближенных вычислений;
– овладение навыками решения линейных, квадратных неравенств, решения неравенств, содержащих переменную величину под знаком модуль;
– овладение умением и навыками доказывать числовых неравенств, применяя свойства числовых неравенств
Обобщающее повторение (9 ч)
Алгебраические дроби. Свойства квадратного корня. Квадратные уравнения. Неравенства.
Цель изучения:
– обобщение и систематизация знаний по алгебре за курс 8 класса;
– формирование понимания возможности использования приобретенных знаний и умений в практической деятельности и повседневной жизни.
Геометрия.
Четырехугольники (14 ч)
Многоугольник. Выпуклый многоугольник. Четырёхугольник.
Параллелограмм. Признаки параллелограмма. Трапеция.
Прямоугольник. Ромб и квадрат. Осевая и центральная симметрии.
В результате изучения учащиеся должны:
- распознавать плоские геометрические фигуры, различать их взаимное расположение, аргументировать суждения, с использованием определений, свойств, признаков;
- изображать планиметрические фигуры;
- выполнять чертежи по условию задач; осуществлять преобразования фигур.
Площадь (14 ч)
Понятие площади многоугольника. Площадь прямоугольника.
Площадь параллелограмма. Площадь треугольника. Площадь трапеции.
В результате изучения учащиеся должны:
- применять полученные знания для вычисления площадей основных геометрических фигур с помощью формул (используя при необходимости справочники и технические средства);
- применять при решении задач теорему Пифагора.
Подобные треугольники (19 ч)
Пропорциональные отрезки. Определение подобных треугольников. Отношение площадей подобных треугольников.
Первый признак подобия треугольников. Второй признак подобия треугольников. Третий признак подобия треугольников.
Средняя линия треугольника. Пропорциональные отрезки в прямоугольном треугольнике. Практические приложения подобия треугольников. О подобии произвольных фигур.
Синус, косинус и тангенс острого угла прямоугольного треугольника. Значения синуса, косинуса и тангенса для углов 30°, 45°, и 60°.
В результате изучения учащиеся должны:
- знать и уметь применять признаки подобия треугольников, теоремы о пропорциональных отрезках;
- проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их прикладного использования;
- знать определения синуса, косинуса, и их значения для углов 30, 45, 60.
Окружность (17 ч)
Взаимное расположение прямой и окружности. Касательная к окружности.
Градусная мера дуги окружности. Теорема о вписанном угле.
Свойства биссектрисы угла и серединного перпендикуляра к отрезку. Теорема о пересечении высот треугольника.
Вписанная окружность. Описанная окружность.
В результате изучения учащиеся должны:
- доказывать и применять при решении задач свойства и признак касательной и секущей, понятие центрального и вписанного углов;
- знать теоремы об окружностях, вписанных и описанных около треугольника и уметь их применять при решении задач, в том числе на доказательство.
Обобщающее повторение (16ч)
Треугольники. Параллельные прямые. Четырёхугольники. Площадь фигур. Подобные треугольники. Окружность. Алгебраические дроби. Действия с алгебраическими дробями. Свойства квадратного корня. Квадратные уравнения. Неравенства. Текстовые задачи.
Задачи на движение. Задачи на работу. Задачи на проценты.
В результате изучения учащиеся должны:
– обобщение и систематизация знаний по геометрии и алгебре за курс 8 класса;
– формирование понимания возможности использования приобретенных знаний и умений в практической деятельности и повседневной жизни.
Учебно-тематический план
| Наименование разделов и тем | Всего часов | В том числе на: |
| уроки | Тестовые работы | Самостоятельные работы | Контрольные работы |
| Алгебраические дроби | 10 | 8 |
| 5 | 2 |
| Повторение | 2 | 2 |
|
|
|
| Четырехугольники | 8 | 8 |
| 3 |
|
| Алгебраические дроби | 11 | 10 | 1 | 5 | 1 |
| Четырехугольники | 6 | 5 | 1 | 2 | 1 |
| Функция 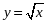 . Свойства квадратного корня. . Свойства квадратного корня. | 18 | 17 | 1 | 12 | 1 |
| Площадь | 14 | 13 | 1 | 4 | 1 |
| Квадратичная функция. Функция у = k/х. | 6 | 5 | 1 | 3 | 1 |
| Подобные треугольники | 8 | 7 |
| 2 | 1 |
| Квадратичная функция. Функция у = k/х. | 11 | 10 | 1 | 7 | 1 |
| Подобные треугольники | 11 | 10 | 1 | 3 | 1 |
| Квадратные уравнения | 9 | 8 |
| 3 | 1 |
| Окружность | 7 | 7 |
| 2 |
|
| Квадратные уравнения | 12 | 11 | 1 | 5 | 1 |
| Окружность | 11 | 10 | 1 | 2 | 1 |
| Неравенства | 15 | 14 |
| 7 | 1 |
| Повторение | 16 | 14 | 4 | 1 | 1 |
|
|
| Итого: | 175 | 159 | 13 | 66 | 15 |
Требования к уровню подготовки выпускников 8 класса
Учащиеся должны знать/понимать:
– значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
– значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии;
– универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности; вероятностный характер различных процессов окружающего мира;
владеть компетенциями: познавательной, коммуникативной, информационной и рефлексивной;
решать следующие жизненно-практические задачи:
– самостоятельно приобретать и применять знания в различных ситуациях;
– работать в группах;
– аргументировать и отстаивать свою точку зрения;
– уметь слушать других; извлекать учебную информацию на основе сопоставительного анализа объектов;
– пользоваться предметным указателем энциклопедий и справочников для нахождения информации;
– самостоятельно действовать в ситуации неопределённости при решении актуальных для них проблем.
Алгебра
должны уметь:
– выполнять арифметические действия, сочетая устные и письменные приемы; находить значения корня натуральной степени, степени с рациональным показателем, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
– составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
– выполнять основные действия со степенями с целыми показателями, с многочленами и алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
– применять свойства арифметических квадратов корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
– решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные уравнения;
– решать линейные и квадратные неравенства с одной переменной и их системы;
– решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
– изображать числа точками на координатной прямой;
– определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;
– находить значения функции, заданной формулой, таблицей, графиком по её аргументу; находить значения аргумента по значению функции, заданной графиком или таблицей;
– определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
– описывать свойства изученных функций, строить их графики;
– извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;
– вычислять средние значения результатов измерений.
Геометрия
должны уметь:
- пользоваться геометрическим языком для описания предметов окружающего мира;
- распознавать геометрические фигуры, различать их взаимное расположение;
- изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразование фигур;
- вычислять значения геометрических величин (длин, углов, площадей), в том числе: определять значение тригонометрических функций по заданным значениям углов; находить значения тригонометрических функций по значению одной из них; находить стороны, углы и площади треугольников, дуг окружности, площадей основных геометрических фигур и фигур, составленных из них;
- решать геометрические задания, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, соображения симметрии;
- проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;
- решать простейшие планиметрические задачи в пространстве.
Критерии и нормы оценки знаний, умений и навыков обучающихся по математике Оценка письменных контрольных работ обучающихся по математике.
Ответ оценивается отметкой «5», если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
Отметка «1» ставится, если:
работа показала полное отсутствие у обучающегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
Оценка устных ответов обучающихся по математике
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна – две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала;
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Отметка «1» ставится, если:
ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изученному материалу.
Перечень учебно- методического обеспечения
УМК
1. Александрова Л. А. Алгебра 8. Самостоятельные работы / Л. А. Александрова. – М.: Мнемозина, 2009.
2. Александрова Л. А. Алгебра 8. Контрольные работы / Л. А. Александрова. – М.: Мнемозина, 2009.
3.Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселёва Л.С., Позняк Э.Г. Геометрия, 7-9 : учеб. для. общеобразоват. учреждений / Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др. – М. : Просвещение, 2009.
4. Атанасян Л.С., Бутузов В.Ф., Глазков Ю.А., Юдина И.И. Геометрия. Рабочая тетрадь для 8 класса : учебное издание для общеобразовательных учреждений / Л.С.Атанасян, В.Ф.Бутузов, Ю.А. Глазков, И.И. Юдина. – М. : Просвещение, 2008.
5. Зив Б.Г. Геометрия : дидактические материалы для 8 класс / Б.Г. Зив, В.М. Мейлер - М. : Просвещение, 2008.
6. Ключникова Е.М. Тесты по алгебре: 8 класс: к учебнику А. Г. Мордкович «Алгебра. 8 класс» / Е.М Ключникова., И.В Комиссарова. - М.: Издательство «Экзамен», 2010.
7. Мордкович А. Г. Алгебра-8. Ч. 1. Учебник / А. Г. Мордкович. – М.: Мнемозина, 2009.
8. Мордкович А. Г. Алгебра-8. Ч. 2. Задачник / А. Г. Мордкович, Т. Н. Мишустина, Е. Е. Тульчинская. – М.: Мнемозина, 2009.
9. Мордкович А. Г. Тесты по алгебре для 7–9 классов / А. Г. Мордкович, Е. Е. Тульчинская. – М.: Мнемозина, 2008.
10. Тульчинская Е.Е. Алгебра-8. Блицопрос / Е. Е. Тульчинская. – М.: Мнемозина, 2008.
Для информационно-компьютерной поддержки учебного процесса предполагается использование следующих программно-педагогических средств, реализуемых с помощью компьютера:
1. CD. АЛГЕБРА 7-11класс. Электронный учебник-справочник .
2. CD. Математика, 5–11классы. Практикум.
3. CD. Открытая математика. Планиметрия. Полный интерактивный курс планиметрии.
4. CD. Открытая математика. Алгебра. Полный интерактивный курс «Алгебра».
5. CD. Открытая математика. Функции и графики. Полный интерактивный курс «Функции и графики».
6. CD. Интерактивные модели на уроках математики.
Для обеспечения плодотворного учебного процесса предполагается использование информации и материалов следующих Интернет-ресурсов:
Министерство образования РФ: http://www.informika.ru/; http://www.ed.gov.ru/; http://www.edu.ru/.
Педагогическая мастерская: http://teacher.fio.ru/; http://www.openklass.ru
Новые технологии в образовании: http://edu.secna.ru/main/.
Путеводитель «В мире науки» для школьников: http://www.uic.ssu.samara.ru/~nauka/.
Мегаэнциклопедия Кирилла и Мефодия: http://mega.km.ru.
Сайты «Мир энциклопедий»: http://www.rubricon.ru/; http://www.encyclopedia.ru/
Список литературы
для учащихся:
1. Крамор, В. С. Задачи с параметрами и методы их решения / В. С. Крамор. – М.: ООО «Издательство “Оникс”»; ООО «Издательство “Мир и Образование”», 2007.
2. Мантуленко, В. Г. Кроссворды для школьников. Математика / В. Г. Мантуленко, О. Г. Гетманенко. – Ярославль: Академия развития, 1998.
3. Энциклопедия. Я познаю мир. Великие ученые. – М.: ООО «Издательство АСТ», 2003.
4. Энциклопедия. Я познаю мир. Математика. – М.: ООО «Издательство АСТ», 2003.
5. Энциклопедия для детей. Математика. Т. 11. – М. : Просвещение, 1998.
для учителя:
1. Алгебра. 8 класс: поурочные планы по учебнику А. Г. Мордковича /авт.- сост. Е.А. Ким. – Волгоград: Учитель, 2008.
2. Арутюнян, Е. Б. Математические диктанты для 5–9 классов / Е. Б. Арутюнян. – М.: Просвещение, 1995.
3. Гаврилова Н.Ф. Геометрия. 8 класс : поурочные планы по учебнику Атанасяна Л.С. и др. / авт. –сост. Н.Ф. Гаврилова. – М.: Просвещение, 2008.
4. Заболотнева, Н. В. Олимпиадные задания по математике: 5–8 классы / Н. В. Заболотнева. – Волгоград: Учитель, 2006.
5. Клименченко, Д. В. Задачи по математике для любознательных / Д. В. Клименченко. – М.: Просвещение, 2007.
6. Математика: еженедельное приложение к газете «Первое сентября».
7. Математика в школе: ежемесячный научно-методический журнал.
8. Мордкович А. Г. Алгебра. 8 класс : методическое пособие для учителя / А. Г. Мордкович. – М. : Мнемозина, 2010.
9. Пичурин, Л. Ф. За страницами учебника алгебры / Л. Ф. Пичурин. – М.: Просвещение, 1990.
Дополнение к рабочей программе
В связи с выпадением часов из-за праздничных дней произведено уменьшение часов за счёт объединения тем раздела «Повторение». Нехватка – 5 часов.
22
















