Рабочая программа Логика для 5-6 классов

Муниципальное бюджетное общеобразовательное учреждение

«Лицей Технополис»

ПРИНЯТО решением методического объединения учителей-предметников образовательных областей «Естественно-научного цикла и математики» ____________________________ от «____» августа 202 года № ___	СОГЛАСОВАНО Заместитель директора по УВР __________________ __________________ от «______» августа 202 года
ПРИНЯТО решением методического объединения учителей-предметников образовательных областей «Естественно-научного цикла и математики» ____________________________ от «____» августа 202 года № ___	СОГЛАСОВАНО Заместитель директора по УВР __________________ __________________ от «______» августа 202 года
ПРИНЯТО решением методического объединения учителей-предметников образовательных областей «Естественно-научного цикла и математики» ____________________________ от «____» августа 202 года № ___	СОГЛАСОВАНО Заместитель директора по УВР __________________ __________________ от «______» августа 202 года

Рабочая программа учебного предмета

«Логика»

для основного общего образования (5 М, 6М класс)

Срок освоения: 2 года

Учебники: Математика 5, 6 класс Дорофеев Г.В., Петерсон Л.Г.

Составитель: Коренева А.В., учитель математики

2022

Пояснительная записка

Рабочая программа учебного курса «Логика» обязательной предметной области «Математика и информатика» для основного общего образования (5-9 классы) является частью основной образовательной программы основного общего образования (далее – ООП ООО) МБОУ «Лицей Технополис» и разработана на основе Федерального государственного образовательного стандарта основного общего образования, Концепции духовно-нравственного развития и воспитания личности гражданина России, планируемых результатов основного общего образования.

 Нормативные документы:

1. Федеральный закон от 29 декабря 2012 г. № 273-ФЗ «Об образовании в Российской Федерации».

2. Постановлением Главного государственного санитарного врача Российской Федерации Постановление от 28 января 2021 г. N 2 Об утверждении санитарных правил и норм САНПИН 1.2.3685-21 "ГИГИЕНИЧЕСКИЕ НОРМАТИВЫ И ТРЕБОВАНИЯ К ОБЕСПЕЧЕНИЮ БЕЗОПАСНОСТИ И (ИЛИ) БЕЗВРЕДНОСТИ ДЛЯ ЧЕЛОВЕКА ФАКТОРОВ СРЕДЫ ОБИТАНИЯ" (Зарегистрировано в Минюсте России 29.01.2021 N 62296).

3. Постановление Главного государственного санитарного врача Российской Федерации от 28.09.2020г. № 28 «Об утверждении санитарных правил СП 2.4.4.3648-20 «Санитарно-эпидемиологические требования к организациям воспитания и обучения, отдыха и оздоровления детей и молодежи»).

4. Приказ Минобрнауки России от 17.12.2010 N 1897 "Об утверждении федерального государственного образовательного стандарта основного общего образования".

5. Приказ Минобрнауки России от 09.06.2016 № 699 "Об утверждении перечня организаций, осуществляющих выпуск учебных пособий, которые допускаются к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования"

6. Основная образовательная программа основного общего образования МБОУ «Лицей Технополис».

 Информационно-методические материалы:

1. Примерная основная образовательная программа основного общего образования (Одобрена решением от 08.04.2015, протокол №1/15 (в редакции протокола № 1/20 от 04.02.2020 – fgosreestr.ru).

2. Примерная основная образовательная программа основного общего образования (Примерная программа по учебному предмету «Математика»)

3. Авторские программы «Математика» (5 6 классы) Л.Г. Петерсон, Г.В. Дорофеев.

Место предмета в учебном плане.

Учебное время на изучение математики в классах, с углубленным изучением отдельных предметов, МБОУ «Лицей Технополис» увеличено за счет части, формируемой участниками образовательных отношений и часов внеурочной деятельности. В 5-6 классах выделены дополнительные часы на изучение курса «Логика», для дополнительной (углубленной) подготовки по предмету. В 5-6 классах за счёт дополнительных часов углубляются межпредметные связи. Математическая логика является основой при построении теорий в математике. На основе понятий простых и сложных высказываний и операций над ними формируется умение проводить логический анализ тех или иных рассуждений. Простые и сложные высказывания исследуются с помощью таблиц истинности, формул алгебры высказываний на выполнимые, противоречивые, тавтологии и др. На основе формул алгебры высказываний учащиеся учатся методам доказательств, строят прямые, обратные, противоположные теоремы, исследуют типы доказательств и теорем на основе имеющихся теорем и высказываний из школьного курса математики.

В 2022-2023 учебном году по календарному учебному графику в 5-6 классах 33 учебные недели.

Общая характеристика курса

Программа курса «Логика» складывается из следующих содержательных компонентов: арифметика; элементы теории множеств.

Содержание раздела «Арифметика» служит базой для дальнейшего изучения обучающимися математики, способствует развитию их логического мышления, формированию умения пользоваться алгоритмами, а также приобретению практических навыков, необходимых в повседневной жизни. Развитие понятия о числе в основной школе связано с рациональными и иррациональными числами, формированием первичных представлений о действительном числе. Завершение числовой линии (систематизация сведений о действительных числах, о комплексных числах), так же, как и более сложные вопросы арифметики (алгоритм Евклида, основная теорема арифметики), отнесены к ступени общего среднего (полного) образования.

При изучении раздела «Элементы теории множеств и математической логики» Обучающиеся научаться решать логические задачи с помощью кругов Эйлера, узнают элементы множества, пустое, конечное, бесконечное множество, подмножество, отношение принадлежности, включения и равенства. Истинность и ложность высказываний. Сложные и простые высказывания.

Особенностями реализации настоящей программы являются:

• изучение логических приемов (сравнение, анализ и синтез, абстрагирование и обобщение);

• требования к формулировке цели задания, выстраиванию цепочки вопросов;

• идея лингвистической коммуникации отражается в постижении основ ораторского искусства. В 5-ом классе у учащихся формируются навыки работы над устным выступлением; 6 класс посвящен изучению основ теории аргументации.

Цели изучения предмета с точки зрения формирования личностных, метапредметных и предметных результатов:

1. в направлении личностного развития:

• интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;

• развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;

• формирование интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;

• воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;

• формирование качеств мышления, необходимых для адаптации в современном информационном обществе;

• развитие интереса к математическому творчеству и математических способностей;

• в метапредметном направлении:

• формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;

• развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;

• формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности;

1. в предметном направлении:

• обеспечение овладения математическими знаниями и умениями, необходимыми для продолжения обучения в основной и старшей школе или иных общеобразовательных учреждениях, изучения смежных дисциплин, применения в повседневной жизни;

• создание фундамента для математического развития, формирования механизмов мышления, характерных для математической деятельности.

Главной целью курса математики в соответствии с требованиями ФГОС ООО являются:

• формирование у учащихся умения учиться;

• развитие их мышления, качеств личности, интереса к математике; создание для каждого ребенка возможности достижения высокого уровня математической подготовки.

Задачами данного курса являются:

• всестороннее развитие ребенка, формирование у него способностей к саморазвитию;

• продолжение формирования у учащихся способностей к организации своей учебной деятельности посредством освоения личностных, познавательных, регулятивных и коммуникативных универсальных учебных действий;

• продолжение приобретения опыта самостоятельной математической деятельности по получению нового знания, его преобразованию и применению;

• формирование специфических для математики качеств мышления, необходимых человеку для полноценного функционирования в современном обществе, и, в частности, логического, алгоритмического и эвристического мышления;

• развитие нравственных качеств, создающих условия для успешного вхождения в культуру и созидательную жизнь общества;

• развитие математического языка и математического аппарата как средства описания и исследования окружающего мира и как основы компьютерной грамотности;

• реализация возможностей математики в формировании научного мировоззрения учащихся, в освоении ими научной картины мира с учетом возрастных особенностей учащихся;

• обеспечение овладения системой математических знаний, умений и навыков, необходимых для повседневной жизни и для продолжения образования в средней школе;

• создание здоровьесберегающей информационно-образовательной среды.

В соответствии со статьей 18 «Печатные и электронные образовательные и информационные ресурсы» Федерального закона от 29.12.2012 №273-ФЗ «Об образовании в Российской Федерации» при реализации данной рабочей программы используются:

учебники из числа входящих в федеральный перечень учебников, допущенных к использованию при реализации имеющих государственную аккредитацию образовательных программ начального общего, основного общего, среднего общего образования

1.1.2.4.1.3.2 Математика 6 класс (в 2 частях) Дорофеев Г.В., Петерсон Л.Г. Общество с ограниченной ответственностью "БИНОМ. Лаборатория знаний"; Акционерное общество "Издательство "Просвещение"

Текущий контроль успеваемости и промежуточная аттестация обучающихся:

Порядок, формы и периодичность текущего контроля и промежуточной аттестации по курсу «Логика» осуществляется согласно Положению о формах, периодичности и порядке текущего контроля успеваемости и промежуточной аттестации учащихся МБОУ «Лицей Технополис». Текущий контроль успеваемости обучающихся осуществляется учителем посредством четырехбалльного оценивания в ходе учебных занятий и контрольных работ.

Планируемые результаты освоения учебного предмета, курса

1.1 Личностные результаты освоения учебного предмета, курса

1. Российская гражданская идентичность (патриотизм, уважение к Отечеству, к прошлому и настоящему многонационального народа России, чувство ответственности и долга перед Родиной, идентификация себя в качестве гражданина России, субъективная значимость использования русского языка и языков народов России, осознание и ощущение личностной сопричастности судьбе российского народа). Осознание этнической принадлежности, знание истории, языка, культуры своего народа, своего края, основ культурного наследия народов России и человечества (идентичность человека с российской многонациональной культурой, сопричастность истории народов и государств, находившихся на территории современной России). Осознанное, уважительное и доброжелательное отношение к истории, культуре, религии, традициям, языкам, ценностям народов России и народов мира.

2. Готовность и способность обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию; готовность и способность осознанному выбору и построению дальнейшей индивидуальной траектории образования на базе ориентировки в мире профессий и профессиональных предпочтений, с учетом устойчивых познавательных интересов.

3. Развитое моральное сознание и компетентность в решении моральных проблем на основе личностного выбора, формирование нравственных чувств и нравственного поведения, осознанного и ответственного отношения к собственным поступкам (способность к нравственному самосовершенствованию; веротерпимость, уважительное отношение к религиозным чувствам, взглядам людей или их отсутствию; знание основных норм морали, нравственных, духовных идеалов, хранимых в культурных традициях народов России, готовность на их основе к сознательному самоограничению в поступках, поведении, расточительном потребительстве; сформированность представлений об основах светской этики, культуры традиционных религий, их роли в развитии культуры и истории России и человечества, в становлении гражданского общества и российской государственности; понимание значения нравственности, веры и религии в жизни человека, семьи и общества). Сформированность ответственного отношения к учению; уважительного отношения к труду, наличие опыта участия в социально значимом труде. Осознание значения семьи в жизни человека и общества, принятие ценности семейной жизни, уважительное и заботливое отношение к членам своей семьи.

4. Сформированность целостного мировоззрения, соответствующего современному уровню развития науки и общественной практики, учитывающего социальное, культурное, языковое, духовное многообразие современного мира.

5. Осознанное, уважительное и доброжелательное отношение к другому человеку, его мнению, мировоззрению, культуре, языку, вере, гражданской позиции. Готовность и способность вести диалог с другими людьми и достигать в нем взаимопонимания (идентификация себя как полноправного субъекта общения, готовность к конструированию образа партнера по диалогу, готовность к конструированию образа допустимых способов диалога, готовность к конструированию процесса диалога как конвенционирования интересов, процедур, готовность и способность к ведению переговоров).

6. Освоенность социальных норм, правил поведения, ролей и форм социальной жизни в группах и сообществах. Участие в школьном самоуправлении и общественной жизни в пределах возрастных компетенций с учетом региональных, этнокультурных, социальных и экономических особенностей (формирование готовности к участию в процессе упорядочения социальных связей и отношений, в которые включены и которые формируют сами Обучающиеся; включенность в непосредственное гражданское участие, готовность участвовать в жизнедеятельности подросткового общественного объединения, продуктивно взаимодействующего с социальной средой и социальными институтами; идентификация себя в качестве субъекта социальных преобразований, освоение компетентностей в сфере организаторской деятельности; интериоризация ценностей созидательного отношения к окружающей действительности, ценностей социального творчества, ценности продуктивной организации совместной деятельности, самореализации в группе и организации, ценности «другого» как равноправного партнера, формирование компетенций анализа, проектирования, организации деятельности, рефлексии изменений, способов взаимовыгодного сотрудничества, способов реализации собственного лидерского потенциала).

7. критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;

8. представление о математической науке как сфере человеческой деятельности, об этапах ее развития, о ее значимости для развития цивилизации;

9. креативность мышления, инициатива, находчивость, активность при решении математических задач;

10. умение контролировать процесс и результат учебной математической деятельности;

11. способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений;

1.2 Метапредметные результаты освоения учебного предмета, курса

Регулятивные УУД

1. Умение самостоятельно определять цели обучения, ставить и формулировать новые задачи в учебе и познавательной деятельности, развивать мотивы и интересы своей познавательной деятельности.

Обучающийся сможет:

• анализировать существующие и планировать будущие образовательные результаты;

• идентифицировать собственные проблемы и определять главную проблему;

• выдвигать версии решения проблемы, формулировать гипотезы, предвосхищать конечный результат;

• ставить цель деятельности на основе определенной проблемы и существующих возможностей;

• формулировать учебные задачи как шаги достижения поставленной цели деятельности;

• обосновывать целевые ориентиры и приоритеты ссылками на ценности, указывая и обосновывая логическую последовательность шагов.

1. Умение самостоятельно планировать пути достижения целей, в том числе альтернативные, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач.

Обучающийся сможет:

• определять необходимые действие(я) в соответствии с учебной и познавательной задачей и составлять алгоритм их выполнения;

• обосновывать и осуществлять выбор наиболее эффективных способов решения учебных и познавательных задач;

• определять/находить, в том числе из предложенных вариантов, условия для выполнения учебной и познавательной задачи;

• выстраивать жизненные планы на краткосрочное будущее (заявлять целевые ориентиры, ставить адекватные им задачи и предлагать действия, указывая и обосновывая логическую последовательность шагов);

• выбирать из предложенных вариантов и самостоятельно искать средства/ресурсы для решения задачи/достижения цели;

• составлять план решения проблемы (выполнения проекта, проведения исследования);

• определять потенциальные затруднения при решении учебной и познавательной задачи и находить средства для их устранения;

• описывать свой опыт, оформляя его для передачи другим людям в виде технологии решения практических задач определенного класса;

• планировать и корректировать свою индивидуальную образовательную траекторию.

1. Умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности в процессе достижения результата, определять способы действий в рамках предложенных условий и требований, корректировать свои действия в соответствии с изменяющейся ситуацией.

Обучающийся сможет:

• определять совместно с педагогом и сверстниками критерии планируемых результатов и критерии оценки своей учебной деятельности;

• систематизировать (в том числе выбирать приоритетные) критерии планируемых результатов и оценки своей деятельности;

• отбирать инструменты для оценивания своей деятельности, осуществлять самоконтроль своей деятельности в рамках предложенных условий и требований;

• оценивать свою деятельность, аргументируя причины достижения или отсутствия планируемого результата;

• находить достаточные средства для выполнения учебных действий в изменяющейся ситуации и/или при отсутствии планируемого результата;

• работая по своему плану, вносить коррективы в текущую деятельность на основе анализа изменений ситуации для получения запланированных характеристик продукта/результата;

• устанавливать связь между полученными характеристиками продукта и характеристиками процесса деятельности и по завершении деятельности предлагать изменение характеристик процесса для получения улучшенных характеристик продукта;

• сверять свои действия с целью и, при необходимости, исправлять ошибки самостоятельно.

1. Умение оценивать правильность выполнения учебной задачи, собственные возможности ее решения.

Обучающийся сможет:

• определять критерии правильности (корректности) выполнения учебной задачи;

• анализировать и обосновывать применение соответствующего инструментария для выполнения учебной задачи;

• свободно пользоваться выработанными критериями оценки и самооценки, исходя из цели и имеющихся средств, различая результат и способы действий;

• оценивать продукт своей деятельности по заданным и/или самостоятельно определенным критериям в соответствии с целью деятельности;

• обосновывать достижимость цели выбранным способом на основе оценки своих внутренних ресурсов и доступных внешних ресурсов;

• фиксировать и анализировать динамику собственных образовательных результатов.

1. Владение основами самоконтроля, самооценки, принятия решений и осуществления осознанного выбора в учебной и познавательной.

Обучающийся сможет:

• наблюдать и анализировать собственную учебную и познавательную деятельность и деятельность других обучающихся в процессе взаимопроверки;

• соотносить реальные и планируемые результаты индивидуальной образовательной деятельности и делать выводы;

• принимать решение в учебной ситуации и нести за него ответственность;

• самостоятельно определять причины своего успеха или неуспеха и находить способы выхода из ситуации неуспеха;

• ретроспективно определять, какие действия по решению учебной задачи или параметры этих действий привели к получению имеющегося продукта учебной деятельности;

• демонстрировать приемы регуляции психофизиологических/ эмоциональных состояний для достижения эффекта успокоения (устранения эмоциональной напряженности), эффекта восстановления (ослабления проявлений утомления), эффекта активизации (повышения психофизиологической реактивности).

Познавательные УУД

1. Умение определять понятия, создавать обобщения, устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации, устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение (индуктивное, дедуктивное, по аналогии) и делать выводы.

Обучающийся сможет:

• подбирать слова, соподчиненные ключевому слову, определяющие его признаки и свойства;

• выстраивать логическую цепочку, состоящую из ключевого слова и соподчиненных ему слов;

• выделять общий признак двух или нескольких предметов, явлений и объяснять их сходство;

• объединять предметы и явления в группы по определенным признакам, сравнивать, классифицировать и обобщать факты и явления;

• выделять явление из общего ряда других явлений;

• определять обстоятельства, которые предшествовали возникновению связи между явлениями, из этих обстоятельств выделять определяющие, способные быть причиной данного явления, выявлять причины и следствия явлений;

• строить рассуждение от общих закономерностей к частным явлениям и от частных явлений к общим закономерностям;

• строить рассуждение на основе сравнения предметов и явлений, выделяя при этом общие признаки;

• излагать полученную информацию, интерпретируя ее в контексте решаемой задачи;

• самостоятельно указывать на информацию, нуждающуюся в проверке, предлагать и применять способ проверки достоверности информации;

• вербализовать эмоциональное впечатление, оказанное на него источником;

• объяснять явления, процессы, связи и отношения, выявляемые в ходе познавательной и исследовательской деятельности (приводить объяснение с изменением формы представления; объяснять, детализируя или обобщая; объяснять с заданной точки зрения);

• выявлять и называть причины события, явления, в том числе возможные /наиболее вероятные причины, возможные последствия заданной причины, самостоятельно осуществляя причинно-следственный анализ;

• делать вывод на основе критического анализа разных точек зрения, подтверждать вывод собственной аргументацией или самостоятельно полученными данными.

1. Умение создавать, применять и преобразовывать знаки и символы, модели и схемы для решения учебных и познавательных задач.

Обучающийся сможет:

• обозначать символом и знаком предмет и/или явление;

• определять логические связи между предметами и/или явлениями, обозначать данные логические связи с помощью знаков в схеме;

• создавать абстрактный или реальный образ предмета и/или явления;

• строить модель/схему на основе условий задачи и/или способа ее решения;

• создавать вербальные, вещественные и информационные модели с выделением существенных характеристик объекта для определения способа решения задачи в соответствии с ситуацией;

• преобразовывать модели с целью выявления общих законов, определяющих данную предметную область;

• переводить сложную по составу (многоаспектную) информацию из графического или формализованного (символьного) представления в текстовое, и наоборот;

• строить схему, алгоритм действия, исправлять или восстанавливать неизвестный ранее алгоритм на основе имеющегося знания об объекте, к которому применяется алгоритм;

• строить доказательство: прямое, косвенное, от противного;

• анализировать/рефлексировать опыт разработки и реализации учебного проекта, исследования (теоретического, эмпирического) на основе предложенной проблемной ситуации, поставленной цели и/или заданных критериев оценки продукта/результата.

1. Смысловое чтение.

Обучающийся сможет:

• находить в тексте требуемую информацию (в соответствии с целями своей деятельности);

• устанавливать взаимосвязь описанных в тексте событий, явлений, процессов;

• резюмировать главную идею текста;

1. Формирование и развитие экологического мышления, умение применять его в познавательной, коммуникативной, социальной практике и профессиональной ориентации.

• определять свое отношение к природной среде;

• анализировать влияние экологических факторов на среду обитания живых организмов;

1. Развитие мотивации к овладению культурой активного использования словарей и других поисковых систем.

Обучающийся сможет:

• определять необходимые ключевые поисковые слова и запросы;

• осуществлять взаимодействие с электронными поисковыми системами, словарями;

• формировать множественную выборку из поисковых источников для объективизации результатов поиска;

• соотносить полученные результаты поиска со своей деятельностью.

Коммуникативные УУД

1. Умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками; работать индивидуально и в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов; формулировать, аргументировать и отстаивать свое мнение.

Обучающийся сможет:

• определять возможные роли в совместной деятельности;

• играть определенную роль в совместной деятельности;

• принимать позицию собеседника, понимая позицию другого, различать в его речи: мнение (точку зрения), доказательство (аргументы), факты; гипотезы, аксиомы, теории;

• определять свои действия и действия партнера, которые способствовали или препятствовали продуктивной коммуникации;

• строить позитивные отношения в процессе учебной и познавательной деятельности;

• корректно и аргументированно отстаивать свою точку зрения, в дискуссии уметь выдвигать контраргументы, перефразировать свою мысль (владение механизмом эквивалентных замен);

• критически относиться к собственному мнению, с достоинством признавать ошибочность своего мнения (если оно таково) и корректировать его;

• предлагать альтернативное решение в конфликтной ситуации;

• выделять общую точку зрения в дискуссии;

• договариваться о правилах и вопросах для обсуждения в соответствии с поставленной перед группой задачей;

• организовывать учебное взаимодействие в группе (определять общие цели, распределять роли, договариваться друг с другом и т. д.);

• устранять в рамках диалога разрывы в коммуникации, обусловленные непониманием/неприятием со стороны собеседника задачи, формы или содержания диалога.

1. Умение осознанно использовать речевые средства в соответствии с задачей коммуникации для выражения своих чувств, мыслей и потребностей для планирования и регуляции своей деятельности; владение устной и письменной речью, монологической контекстной речью.

Обучающийся сможет:

• определять задачу коммуникации и в соответствии с ней отбирать речевые средства;

• отбирать и использовать речевые средства в процессе коммуникации с другими людьми (диалог в паре, в малой группе и т. д.);

• представлять в устной или письменной форме развернутый план собственной деятельности;

• соблюдать нормы публичной речи, регламент в монологе и дискуссии в соответствии с коммуникативной задачей;

• высказывать и обосновывать мнение (суждение) и запрашивать мнение партнера в рамках диалога;

• принимать решение в ходе диалога и согласовывать его с собеседником;

• создавать письменные «клишированные» и оригинальные тексты с использованием необходимых речевых средств;

• использовать вербальные средства (средства логической связи) для выделения смысловых блоков своего выступления;

• использовать невербальные средства или наглядные материалы, подготовленные/отобранные под руководством учителя;

• делать оценочный вывод о достижении цели коммуникации непосредственно после завершения коммуникативного контакта и обосновывать его.

1. Формирование и развитие компетентности в области использования информационно-коммуникационных технологий (далее – ИКТ).

Обучающийся сможет:

• целенаправленно искать и использовать информационные ресурсы, необходимые для решения учебных и практических задач с помощью средств ИКТ;

• выбирать, строить и использовать адекватную информационную модель для передачи своих мыслей средствами естественных и формальных языков в соответствии с условиями коммуникации;

• выделять информационный аспект задачи, оперировать данными, использовать модель решения задачи;

• использовать компьютерные технологии (включая выбор адекватных задаче инструментальных программно-аппаратных средств и сервисов) для решения информационных и коммуникационных учебных задач, в том числе: вычисление, написание писем, сочинений, докладов, рефератов, создание презентаций и др.;

• использовать информацию с учетом этических и правовых норм;

• создавать информационные ресурсы разного типа и для разных аудиторий, соблюдать информационную гигиену и правила информационной безопасности.

1.3 Предметные результаты освоения учебного предмета, курса Математика (изучение на базовом и углубленном уровне)

5 класс

Пятиклассник научится:

Владеть понятиями:

1) математическая модель;

2) высказывания и общие утверждения;

3) тема, рема высказываний;

4) элемент множества;

5) равносильность предложений.

Пятиклассник получит возможность научится:

1) переводить условие задачи на математический язык;

2) составлять математическую модель;

3) проверять правильность рассуждений с помощью логического следствия;

4) применять изученный аппарат исследования к теоретическим высказываниям в школьном курсе математики;

5) выделять тему и рему высказываний;

6) обосновывать решение логических задач.

6 класс

Шестиклассник научится:

Владеть понятиями:

1) логические операции: конъюнкция, дизъюнкция, импликация, эквиваленция, отрицание;

2) формула алгебры высказываний, законы логики;

3) таблица истинности;

4) диаграмма Эйлера-Венна;

5) необходимое условие, достаточное условие, необходимое и достаточное условие;

6) логическое следование.

Шестиклассник получит возможность научится:

1) владеть соответствующим понятийно-терминологическим аппаратом;

2) уметь собирать, группировать и преподносить материал;

3) строить таблицы истинности;

4) уметь доказывать равносильность формул алгебры высказываний;

5) выработать умение строить умозаключения;

6) выработать навыки аргументации;

8) решать задачи с помощью кругов Эйлера.

2. СОДЕРЖАНИЕ УЧЕБНОГО ПРЕДМЕТА

Главной задачей обучения математике становится формирование у учащихся в процессе обучения качеств мышления, деятельностных способностей и системы ценностей, необходимых для полноценного функционирования человека в современном обществе, динамичной адаптации человека к этому обществу, самоопределения и самореализации.

Таким образом, с точки зрения приоритета развивающей функции образования в «математике для каждого» конкретные математические знания рассматриваются не как самоцель, а как база, «полигон» для организации полноценной учебной деятельности учащихся.

В новых социальных условиях широкого развития информационных сетей приоритетное значение умение найти информацию, проанализировать, продуцировать и использовать для решения практической задачи.

Поэтому конкретное содержание обучения математике в программе подчинено задаче общеинтеллектуального и общекультурного развития учащихся и использованию математики в повседневной жизни.

Учебно-воспитательный процесс строится в соответствии с общими целями современного образования, основными этапами процесса познания и возрастными особенностями учащихся, их психофизиологическими и социокультурными характеристиками.

В связи с этим отличительным свойством данного периода (6 класс) является формирование абстрактного мышления, включающего в себя не только умение воспринимать специфические, свойственные математике абстрактные объекты и конструкции, но и умение оперировать с такими объектами и конструкциями по предписанным правилам. Необходимой компонентой абстрактного мышления является логическое мышление как дедуктивное, в том числе и аксиоматическое, так и продуктивное эвристическое и алгоритмическое.

В процессе изучения математики в наиболее чистом виде могут быть сформированы не только логическое и алгоритмическое мышление, но и многие важнейшие качества мышления, такие, как сила, гибкость, глубина, конструктивность, критичность и др.

Параллельно с формированием мышления на этапе обучения в средней школе оформляются коммуникативные способности обучающихся и их способности к учебной деятельности (умение учиться). Обучающиеся осваивают нормы доказательных рассуждений и рефлексивной самоорганизации и начинают их применять для решения учебных и жизненных проблем.

Данный курс рассчитан на развитие навыков, позволяющих подготовить учащихся к освоению логических знаний, а также на формирование общеучебных умений (исходя из особой вторичной значимости курса).

В основу курса легла идея Н.С.Лейтеса о способностях, обеспечивающих успешность выполнения умственной деятельности:

1) внимательность;

2) готовность к труду;

3) мыслительная деятельность (быстрота мыслительных процессов, систематичность, повышение уровня анализа, обобщения).

Предложенная программа включает РАЗДЕЛЫ:

1) Логика, как наука.

2) Математические модели.

3) Язык и логика.

4) Азбука рассуждений, истина, ложь.

5) Решение логических задач.

Математические модели

Числовые и алгебраические выражения. Что такое математический язык. Что такое математическая модель. Линейное уравнение с одной переменной. Задачи на составление линейных уравнений с одной переменной. Данные и ряды данных. Координатная прямая.

Обучающиеся повторяют темы: Делимость натуральных чисел. Понятие делимости. Признаки и свойства делимости. Делимость и остатки. Некоторые теоремы теории делимости. Основная теорема арифметики. Решают задачи и примеры на числовые и алгебраические выражения, допустимые значения переменных, входящих в алгебраические выражения, равенство буквенных выражений, тождество. Учатся стоить математическую модель. Решать линейное уравнение с одной переменной, приводящихся к линейным.

Язык и логика

Понятие отрицания. Противоречие. Отрицание общих высказываний. Отрицание высказываний о существовании. Способы выражения отрицания общих высказываний и высказываний о существовании в естественном языке.

Алгебраические выражения. Понятие переменной величины. Выражения с переменными. Предложения с переменными. Переменная и кванторы. Отрицание утверждений с кванторами.

Основная содержательная цель сформировать представление об отрицании высказываний, умение строить отрицания частных высказываний, общих высказываний и высказываний о существовании; уточнить понятия переменной, выражения с переменной и предложения с переменной; научить использовать кванторы и для записи высказываний и их отрицаний; повторить действия с обыкновенными и десятичными дробями. Программа 6 класса начинается со знакомства учащихся с отрицанием высказывания как с предложением, в котором выражается противоположное мнение. Логическим эквивалентом отрицания является оборот «неверно, что...» или просто частица «не».

От простейших случаев отрицания Обучающиеся переходят к более сложным случаям построению отрицаний общих высказываний и высказываний о существовании. Выявляется их важнейшее общее свойство, а именно то, что отрицание общего высказывания есть высказывание о существовании, и наоборот. Правильность построения отрицаний проверяется с помощью закона исключенного третьего.

Уточняется понятие переменной. Обучающиеся знакомятся с использованием логических символов кванторов существования и для записи высказываний и их отрицаний, используют буквы для обозначения чисел, вычисляют значения алгебраического выражения, применяют алгебраические выражения для записи свойств арифметических действий, преобразовывают алгебраические выражения.

Все вопросы, связанные с высказываниями, рассматриваются как на примерах из жизни, так и на математических объектах.

Азбука размышлений

Понятие логического следования. Отрицание следования. Обратное утверждение. Следование и равносильность. Следование и свойства предметов.

Основная содержательная цель познакомить с понятиями логического следования и его отрицания, обратного утверждения, характеристического свойства (признака), научить в простейших случаях выполнять их построение.

В данной теме формируются представления о логическом следовании и логическом выводе, достаточные для последующего рассмотрения геометрического материала и мотивации деятельности учащихся на уроках геометрии в 7 классе. При этом новые логические понятия, с одной стороны, помогают повторять и закреплять материал, изученный ранее, а с другой стороны, подготавливают к изучению следующих разделов программы.

ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ

5 класс 2 ч в неделю, 33 недель, всего 66 ч

№	Тема	Кол-во час	Деятельность учителя с учетом рабочей программы воспитания
1	Логика как наука	1	устанавливать доверительные отношения между учителем и обучающимися, способствующих позитивному восприятию учащимися требований и просьб учителя
2	Перевод условия задачи на математический язык	1	привлекать внимание обучающихся к обсуждаемой на уроке информации, активизации познавательной деятельности обучающихся побуждать обучающихся соблюдать на уроке общепринятые нормы поведения, правила общения со старшими (учителями) и сверстниками (обучающимися)
3	Составление математических моделей	2
4	Метод проб и ошибок.	3
5	Метод перебора	3
6	Контрольная работа №1	1	побуждать обучающихся соблюдать на уроке принципы учебной дисциплины и самоорганизации
7	Высказывания и утверждения	3	привлекать внимание обучающихся к ценностному аспекту изучаемых на уроке явлений, понятий, приемов организовывать работу обучающихся с социально значимой информацией по поводу получаемой на уроке социально значимой информации – обсуждать, высказывать мнение
8	«Хотя бы один»	2
9	Доказательство общих утверждений	3
10	Введение обозначений.	3
11	Равносильность предложений	2
12	Контрольная работа №2	1	побуждать обучающихся соблюдать на уроке принципы учебной дисциплины и самоорганизации
13	Логика и рассуждения	4	инициировать обучающихся к обсуждению, высказыванию своего мнения, выработке своего к отношения по поводу получаемой на уроке социально значимой информации Использовать воспитательные возможности содержания учебного предмета через демонстрацию обучающимся примеров ответственного, гражданского поведения, проявления человеколюбия и добросердечности
14	Основные методы решения логических задач	4
15	Решение задач о лгунах	4
16	Задачи на соответствие и исключение.	4
17	Решение задач на переливание.	4
18	Решение задач на взвешивание.	4
19	Решение задач с конца.	4
20	Решение логических задач табличным способом.	4
21	Логические головоломки разных видов.	4
22	Решение логических задач повышенной трудности.	4
23	Итоговая контрольная работа	1	побуждать обучающихся соблюдать на уроке принципы учебной дисциплины и самоорганизации

ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ

6 класс (1 час в неделю, 33 недели, всего 33 часа)

№	Тема	Количество часов	Деятельность учителя с учетом рабочей программы воспитания
	Виды вопросов. Корректные и некорректные вопросы	1	устанавливать доверительные отношения между учителем и обучающимися, способствующих позитивному восприятию учащимися требований и просьб учителя привлекать внимание обучающихся к обсуждаемой на уроке информации, активизации познавательной деятельности обучающихся
	Пересечения, объединения или дополнения	1
	Круговые схемы Эйлера	1
	Силлогизмы на кругах Эйлера	1
	Суждение, структура суждения. Виды суждений	1
	Условные суждения	1
	Отношения между суждениями	1
	Логический квадрат	1
	Умозаключение, виды умозаключений	1
	Умозаключения с союзом «или», «если… то»	1
	Индукция. Правила индукции. Ошибки индукции	1
	Аналогия. Правила аналогии	1
	Основные законы логики	1
	Закон тождества. Закон противоречия	1
	Закон исключенного третьего	1	привлекать внимание обучающихся к обсуждаемой на уроке информации, активизации познавательной деятельности обучающихся
	Контрольная работа	1
	Отрицание высказывания, проверка закона исключенного третьего	1
	Закон достаточного основания	1
	Решение логических задач, проверка закона достаточного основания	1
	Софизмы и парадоксы	1
	Парадоксы-антиномии	1
	Парадокс «Протагор и Эватл»	1
	Парадоксы-апории	1
	Противоречия, абсурды	1
	Логические противоречия	1	побуждать обучающихся соблюдать на уроке принципы учебной дисциплины и самоорганизации привлекать внимание обучающихся к ценностному аспекту изучаемых на уроке явлений, понятий, приемов
	Доказательства и опровержения	1
	Ложные дихотомии	1
	Причинно-следственная связь	1
	Доказательство. Структура доказательства	1
	Прямые и косвенные доказательства	1
	Виды и методы подтверждения/опровержения	1
	Контрольная работа	1
	Истинность и достаточность аргументов в доказательствах	1

Литература для учителя:

1. Босс В. Лекции по математике. Т. 6: От Диофанта до Тьюринга. - М.: КомКнига, 2006. - 208 с.

2. Босс В. Лекции по математике. Т. 10: Перебор и эффективные алгоритмы: Учебное пособие. — М.: Издательство ЛКИ, 2008. — 216 с.

3. Клини С.К. Математическая логика. - М., Мир, 1973.- 480 с.

Литература для учащихся:

1. Г.В. Дорофеев, Л.Г. Петерсон. Математика 5 класс 1 часть. – М.: «Ювента», 2011 г. – 176 с.

2. Г.В. Дорофеев, Л.Г. Петерсон. Математика 5 класс 2 часть. – М.: «Ювента», 2011 г. – 240 с.

3. Л.М. Лоповок «1000 проблемных задач по математике», 1995 г.

4. М.А. Кубышева «Сборник самостоятельных и контрольных работ к учебникам математики 5-6 классов Г.В. Дорофеева, Л.Г. Петерсон. – М.: УМЦ «Школа 2000…», 2007. – 80 с.

ПРИЛОЖЕНИЕ

Задачи для V класса

Задача 1. Землекопы.

Пять землекопов за 5 часов выкапывают 5 метров канавы. Сколько землекопов выкопают 100 метров канавы за 100 часов?

Ответ. 5 землекопов.

Задача 2. Три и семь.

Часы бьют три, и, пока они бьют, проходит 3 секунды. Сколько времени

пройдет, пока часы будут бить семь.

Ответ. 9 секунд.

Задача 3. Сотня орехов.

Сотню орехов надо разделить между 25 людьми так, чтобы никому не досталось четное число орехов. Можете ли вы это сделать? “Съесть” орех нельзя.

Ответ. Задача не имеет решения.

Задача 4. Три друга.

Три друга – Алеша, Коля и Саша – сели на скамейку в один ряд. Сколькими способами они могли это сделать?

Ответ. Друзья могли сесть 6 способами: 1) Алеша, Коля, Саша; 2) Алеша, Саша, Коля; 3) Коля, Алеша, Саша; 4) Коля, Саша, Алеша; 5) Саша, Алеша, Коля; 6) Саша, Коля. Алеша.

Задача 5. Рейс через океан.

Каждый день в полдень из Гавра в Нью-Йорк отправляется пароход через Атлантический океан, и в то же самое время пароход той же компании отправляется из Нью-Йорка в Гавр. Переезд в том и другом направлении совершается ровно за семь, дней. Сколько судов своей компании, идущих в противоположном направлении, встречает пароход на пути из Гавра в Нью-Йорк?

Ответ. Пароход встречает 15 судов.

Задача 6. Какая цифра?

Догадайтесь, какая цифра в выражении заменена буквой А:

9А : 1А = А.

Ответ. Цифра 6.

Задача 7. Почем дюжина лимонов?

Три дюжины лимонов стоят столько рублей, сколько дают лимонов на 16 рублей. Сколько стоит дюжина лимонов? (Одна дюжина =12.)

Ответ. Дюжина лимонов стоит 8 рублей.

Задача 8. Плащ, шляпа и калоши.

Купец купил плащ, шляпу и калоши и заплатил за все 140 рублей. Плащ стоит на 90 рублей больше, чем шляпа, а шляпа и плащ вместе на 120 рублей больше, чем калоши Сколько стоит каждая вещь в отдельности?

Задачу требуется решить устным счетом, без уравнений.

Ответ. Калоши стоят 10 рублей, шляпа – 20 рублей, плащ– 110 рублей.

Задача 9. Пильщики дров.

Пильщики распиливают бревно на метровые обрубки. Длина бревна – 5 метров. Распиловка бревна поперек отнимает каждый раз полторы минуты. Сколько минут потребуется, чтобы распилить все бревно?

Ответ. Для распиловки бревна потребуется 6 минут.

Задача 10. Из семи цифр.

Пусть записано подряд семь цифр от 1 до 7:

1234567.

Легко соединить их знаками “плюс” и “минус” так, чтобы получилось 40:

12 + 34-5 + 6-7 = 40

Попробуйте найти другие расстановки знаков между теми же цифрами, при которых получилось бы не 40, а 55.

Ответ.

123 + 4-5-67 = 55;

1-2-3-4 + 56 + 7 = 55;

12- 3 + 45 -6 + 7 = 55,

Возможно, учащиеся смогут найти и другие варианты ответов.

Задача 11.Четырьмя двойками.

Можно ли четырьмя двойками выразить число 111?

Ответ. Можно: 222/2 =111.

Задача 12. Турист.

За 1 час турист проходит 6 км. Сколько метров он проходит за 1 минуту? Сколько сантиметров за 1 секунду?

Ответ. За 1 минуту турист проходит 100 м; за 1 секунду примерно 17см.

Задача 13. Четырьмя способами.

Выразите число 100 пятью одинаковыми цифрами. Предложите четыре способа решения.

Ответ.

111 - 11 = 100;

33^.3 + 3/3 = 100;

5^.5^.5 – 5^.5= 100;

(5 -5 + 5 + 5 )^.5 = 100.

Задача 14. Числовой ребус.

Разгадайте числовой ребус:

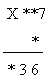
Ответ. 117*8 = 936.

Задача 15. Переливание молока.

Перед вами кувшин, содержащий 4 литра молока. Вам необходимо разделить эти 4 литра поровну между двумя друзьями, но из посуды у вас имеются только еще два пустых кувшина: один, вмещающий 3 литра, и другой, вмещающий 1 литр. Как же поделить молоко поровну с помощью только этих трех сосудов? Придется, конечно, несколько раз переливать молоко из сосуда в сосуд. Но как?

Задача 16. Столяр и плотник.

Бригада из шести плотников и столяра взялась выполнить некоторую работу. Каждый плотник заработал по 20 рублей, столяр же – на 3 рубля больше, чем заработал в среднем каждый из семерых членов бригады. Сколько заработал столяр?

Ответ. Столяр заработал 23 рубля 50 копеек.

Задача 17. Яблоки.

Разделить 9 яблок поровну между 12 школьниками, причем ни одно яблоко не разрезать более чем на четыре части.

Задача 18. Число 66.

Число 66 надо увеличить в полтора раза, не производя над ним никаких арифметических действий. Как это сделать?

Ответ. Нужно написанное число 66 перевернуть “вверх ногами”.

Задача 19. Чистка картофеля.

Двое очистили 400 картофелин: один очищал три картофелины в минуту, другой – две. Второй работал на 25 минут больше первого. Сколько времени работал каждый?

Ответ. Первый работал 70 минут, второй – 95 минут.

Задача 20. Пятью двойками. Можно ли пятью двойками выразить число 28?

Ответ. Можно: 22+ 2 + 2 + 2= 28.

Задача 21 .Переливание воды.

Как с помощью пятилитровой и трехлитровой банок налить из крана в ведро ровно 4 литра воды?

Задача 22. Переливание молока.

Как с помощью двух бидонов емкостью 5 литров и 8 литров отлить из молочной цистерны 7 литров молока?

Задача 23. Последняя цифра.

Какой цифрой оканчивается произведение 13 *14*15* 16*17?

Ответ. Произведение оканчивается нулем.

Задача 24. Подберите три числа.

Из чисел 21, 19, 30, 25, 3. 12, 9, 15. 6. 27 подберите такие три числа, сумма которых будет равна 50.

Ответ. Надо взять числа 19, 6, 25.

Задача 25. Имя девочки.

В семье трое детей – два мальчика и одна девочка. Их имена начинаются с букв А. В и Г. Среди имен, начинающихся с букв А и В, есть имя одного мальчика. Среди имен, начинающихся с букв В и Г, также есть имя одного мальчика. С какой буквы начинается имя девочки?

Ответ. Имя девочки начинается с буквы В.

Задача 26. Поросята и Волк.

Поросята Ниф-Ниф и Нуф-Нуф бежали от Волка к домику Наф-Нафа. Волку бежать до поросят (если бы они стояли на месте) 4 минуты. Поросятам бежать до домика Наф-Нафа 6 минут. Волк бежит в 2 раза быстрее поросят. Успеют ли поросята добежать до домика Наф-Нафа?

Ответ. Поросята успеют добежать до домика Наф-Нафа.

Задача 27. Сколько машин?

В мастерской отремонтировано в течение месяца 40 машин – автомобилей и мотоциклов. Всех колес было выпущено из ремонта ровно 100. Сколько было в ремонте автомобилей и мотоциклов?

Ответ. В ремонте было 10 автомобилей и 30 мотоциклов.

Задача 28. Шесть двоек.

Используя 6 раз цифру 2, знаки арифметических операций и скобки, запишите выражение, значение которого равно 100.

Ответ. (222 - 22) : 2 = 100.

Задача 29. Единица.

Выразите единицу, употребив все 10 цифр.

Ответ. Возможны различные варианты решения:

Задача 30. Малыш, Карлсон и варенье.

Малыш может съесть 600 граммов варенья за 6 минут, а Карлсон – в 2 раза быстрее. За какое время они съедят это варенье вместе?

Ответ. Малыш и Карлсон вместе съедят варенье за 2 минуты.

Задача 31 .Три богатыря и великаны.

Илья Муромец, Добрыня Никитич и Алеша Попович вступили в бой с несколькими великанами. Каждый великан получил по 3 удара богатырскими палицами, в результате все великаны обратились в бегство. Больше всего ударов нанес Илья Муромец – 7, меньше всего Алеша Попович – 3. Сколько всего было великанов?

Ответ. Всего было 5 великанов.

Задача 32. Двое рабочих.

Двое рабочих могут выполнить некоторую работу за 7 дней при условии, что второй приступит к ней 2 днями позже первого. Если бы ту же работу каждый выполнял в отдельности, то первому понадобилось бы на 4 дня больше, чем второму. За сколько дней каждый мог бы единолично выполнить эту работу?

Задача допускает чисто арифметическое решение, причем можно обойтись даже без действий с дробями.

Ответ. Первый рабочий мог бы единолично выполнить работу за 14 дней, второй – за 10 дней.

Задача 33. Путешественники и разбойники.

К реке, у берега которой находилась лодка, вмещающая только двух человек, подошли два разбойника и два путешественника. Разбойники не решались напасть на путешественников. Они могли бы совершить нападение, только если на берегу остались бы два разбойника и один путешественник. У одного из разбойников была сломана рука, и он даже не мог грести веслами. Как надо переправиться через реку разбойникам и путешественникам, чтобы последние избежали нападения?

Задача 34. Часы.

Известно, что часы за каждые сутки убегают вперед на 3 минуты. Их поставили точно. Через какое время стрелки часов будут снова показывать точное время?

Ответ. Часы снова покажут точное время через 240 суток.

Задачи для VI класса

Задача 1. Покупка фруктов.

За 5 рублей куплено 100 штук разных фруктов. Цены на фрукты следующие: арбузы – 50 копеек за штуку, яблоки – 10 копеек за штуку, сливы – 10 копеек за десяток.

Сколько фруктов каждого рода было куплено?

Ответ. 1 арбуз (50 копеек], 39 яблок (3 рубля 90 копеек), 60 слив (60 копеек).

Задача 2. Подорожание и подешевление. Товар на 10% подорожал, потом на 10% подешевел. Когда цена его была ниже: до подорожания или после подешевления?

Ответ. После подешевления товар стал на 1% дешевле, чем до подорожания.

Задача 3. Бочонки с квасом.

В магазин доставили 6 бочонков с квасом, в них было 15, 16, 18, 19, 20 и 31 литр. В первый же день нашлось два покупателя: один купил два бочонка, другой – три, причем первый купил вдвое меньше кваса, чем второй. Не пришлось даже раскупоривать бочонки. Из шести бочонков на складе остался всего лишь один. Какой?

Ответ. Первый покупатель купил 15-литровый и 18-литровый бочонки.

Второй – 16-литровый, 19-литровый и 31-литровый. Остался непроданным 20-литровый бочонок.

Задача 4. Миллион изделий.

Изделие весит 89,4 грамма. Сообразите в уме, сколько тонн весит миллион таких изделий.

Ответ. Миллион изделий весит 89,4 тонны.

Задача 5. Мед и керосин.

Банка с медом весит 500 граммов. Та же банка с керосином весит 350 граммов. Керосин легче меда в 2 раза. Сколько весит пустая банка?

Ответ Пустая банка весит 200 граммов.

Задача 6. Вес бревна.

Круглое бревно весит 30 килограммов. Сколько бы оно весило, если бы било вдвое толще, но вдвое короче?

Ответ. Бревно весило бы 60 килограммов.

Задача 7. Про Кощея Бессмертного и Змея Горыныча.

Чтобы сжить с белого света Змея Горыныча, которому исполнилось 40 лет, Кощей Бессмертный придумал приучить его к курению. Кощей Бессмертный подсчитал, что если Змей Горыныч каждый день в течение года будет выкуривать по 17 сигарет, то он умрет через 5 лет, если же он будет выкуривать по 16 сигарет, то умрет через 10 лет. До скольких лет доживет Змей Горыныч, если он не будет курить?

Ответ. Некурящий Змей Горыныч проживет до 130 лет.

Задача 8. Кошки и котята.

Четыре кошки и 3 котенка весят 15 килограммов, а 3 кошки и 4 котенка весят 13 килограммов. Предполагается, что все взрослые кошки весят одинаково и котята также весят одинаково. Сколько весит каждая

кошка и каждый котенок в отдельности?

Ответ. Кошка весит 3 килограмма, котенок – 1 килограмм.

Задача 9. Кубики, раковина и бусины.

На чашечных весах 3 кубика и 1 морская раковина уравновешиваются 12 бусинами, а 1 раковина уравновешивается 1 кубиком и 8 бусинами. Сколько бусин надо положить на свободную чашку весов, чтобы уравновесить раковину на другой чашке?

Ответ. Надо положить 9 бусин.

Задача 10. Вес фруктов.

Три яблока и 1 груша весят столько же, сколько 10 персиков, а 6 персиков и 1 яблоко весят столько же, сколько 1 груша. Сколько же персиков надо взять, чтобы уравновесить 1 грушу?

Ответ. Надо взять 7 персиков.

Задача 11. П о обе стороны шести.

Я взглянул на часы и заметил, что обе стрелки отстоят от цифры 6 одинаково по обе ее стороны. В котором часу это было?

Задача 12. Наследство.

В Древнем Риме философы-законники любили задавать друг другу такую задачу. Вдова обязана оставшееся после мужа наследство в 3500 золотых разделить с ребенком, который должен родиться. Если это будет сын, то мать по римским законам получает половину сыновней доли. Если родится дочь, то мать получает двойную долю дочери. Но случилось так, что родились близнецы – сын и дочь. Как следует разделить наследство, чтобы были выполнены все требования закона?

Ответ. Вдова должна получить 1000 золотых, сын – 2000 золотых, дочь – 500 золотых. Тогда требования закона будут выполнены, потому что вдова получит вдвое меньше сына и вдвое больше дочери.

Задача 13. Три разведчика.

В затруднительном положении оказались однажды трое пеших разведчиков, которым необходимо было перебраться на противоположный берег реки при отсутствии моста. Правда, по реке катались в лодке два мальчика, готовые помочь солдатам, Но лодка была так мала, что могла выдержать вес только одного солдата; даже солдат и один мальчик не могли одновременно сесть в нее без риска ее потопить. Плавать солдаты совсем но умели. Казалось бы, при таких условиях мог переправиться через реку только один солдат. Между тем все три разведчика вскоре благополучно переправились на противоположный берег и возвратили лодку мальчикам. Как это они сделали?

Задача 14. Девять цифр.

Напишите по порядку девять цифр:

1 23456789.

Сможете ли вы, не меняя порядка цифр, вставить между ними знаки плюс и минус таким образом, чтобы в результате получилось ровно 100?

Ответ:123-45-67 + 89 = 100.

Задача 15. Пятью двойками.

В вашем распоряжении пять двоек и любые знаки математических операций. Вы должны с помощью только этого цифрового материала, используя его полностью и применяя знаки математических операций, выразить числа 15, 11, 12321.

Ответ.

(2 + 2)²- 2/2 = 15;

(2*2)²- 2/2= 15;

2²⁺² - 2/2 = 15; 22/2 + 2*2= 15;

22/2 + 2² = 15; 22/2 + 2 + 2 = 15;

22/2 + 2-2 = 11;

(222/2)²= 111²= 12321.

Задача 16. Пятью тройками.

Вы, конечно, знаете, что пятью тройками и знаками математических операций можно записать число 100:

33-3 + 3/3 = 100. Но можно ли записать пятью тройками число 10?

Ответ.

33/3 ^. 3/3= 10;

(3*3*3 + 3)/3=10;

3³/3 + 3/3 = 10.

В первом варианте можно использовать любые цифры и вы получите такой же результат:

1 1/1 - 1/1 = 22/2 - 2/2 = 44/4 - 4/4 = ... = 99/9 - 9/9.

Задача 17. Четырьмя тройками.

Очень легко выразить четырьмя тройками число 12: 12 = 3 + 3 + 3 + 3.

Немного сложнее составить подобным же образом из четырех троек числа 15 и 18:

15 = (3 + 3) + (3*3);

18 = (3*3) + (3*3).

Но если бы потребовалось выразить тем же образом – четырьмя тройками – число 5, вы. вероятно, не сразу догадались бы, что 5= (3 + 3)/3 + 3.

Попробуйте теперь сами отыскать способы, как составить из четырех троек числа 1, 2, 3, 4, 6.

Ответ.

1 = 33/33;

2 = 3/3 + 3/3;

3 = (3 + 3 + 3)/3;

4 = (3*3 + 3)/3; 6 = (3 + 3)*3/3.

Можно привести еще решения, используя другие комбинации троек.

Задача 18. Недостающие цифры.

В этом примере умножения столбиком больше половины цифр удалил

шкодливый учащийся и заменил числа звездочками:

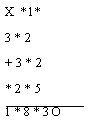
Восстановите недостающие цифры

Ответ.

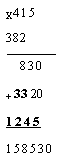
Задача 19. Кто разбил окно?

Один из пяти братьев – Андрей, Витя, Дима, Толя или Юра разбил окно. Андрей сказал: “Это сделал или Витя, или Толя”. Витя сказал: “Это сделал не я и не Юра”. Дима сказал: “Нет, один из них сказал правду, а другой – неправду”. Юра сказал: “Нет, Дима, ты не прав”. Их отец, которому, конечно, можно доверять, уверен, что не менее трех братьев сказали правду. Кто же из братьев разбил окно?

Ответ. Окно разбил Толя.

Задача 20. Замените на цифры.

Замените буквы цифрами так, чтобы результат сложения соответствовалдействительности, учитывая при этом, что одинаковые буквы соответствуютодинаковым цифрам и каждая буква соответствует какой-либо цифре:

удар
+
удар
драка

Ответ. 8126 + 8126 = 16 252.

Задача 21 .Какое число больше? Какое число больше: 4⁴⁴ или 4⁴ ?

4?

Ответ. 4⁴⁴ больше, чем 4⁴, так как 4⁴ = 4²⁵⁶.

Задача 22. Расставьте пингвинов.

Пингвины расположились на солнышке, как изображено на схеме;

П1	П6	П4
	П2
П5	П7	ПЗ

Расставьте их так, чтобы сумма проставленных чисел в горизонтальных. вертикальном и диагональных рядах составляла 12.

Ответ.

П6	П1	П5
	П4
ПЗ	П7	П2

Задача 23. Пять из двенадцати

В самый разгар дискотеки в зале появились пираты с плакатом, на котором было написано 12 чисел:

111

333

777

999

Они предложили присутствующим убрать пять чисел, заменив их при необходимости нулями, и расставить знаки математических операций, чтобы получилось число 1111. “Если вы ото не сделаете за 30 минут, мы вас всех отправим на корабль и увезем в другую страну”, – заявили пираты. Перепуганные посетители дискотеки смогли это сделать и избежать пленения. А вы успеете это сделать за то же время?

Ответ.

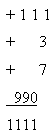
Возможны и другие варианты решения.

Задача 24. Попробуйте сложить.

Возьмите все цифры от 1 до 9, расположите их в две колонки так, чтобы сумма чисел в каждой колонке была одинаковой. Эта задача требует нестандартного мышления.

Задача 25. Сколько кошек?

В комнате четыре угла. В каждом углу сидит кошка. Напротив каждой кошки по три кошки. На хвосте каждой кошки по одной кошке. Сколько всего кошек в комнате?

Ответ. В комнате четыре кошки.

Задача 26. Портной.

У портного есть кусок сукна длиной 16 метров, от которого он отрезает ежедневно по 2 метра. По истечении скольких дней он отрежет последний кусок?

Ответ. Последний кусок будет отрезан по истечении 7 дней.

Задача 27. Продажа яблок.

Фермер привез на рынок корзину яблок. Первому покупателю он продал половину всех яблок и еще пол-яблока, второму – половину остатка и еще пол-яблока и т. д. Когда же пришел шестой покупатель и купил у фермера половину оставшихся яблок и пол-яблока, то оказалось, что у него, как и у всех покупателей, все яблоки были целые и что фермер продал все свои яблоки. Сколько яблок фермер привез на рынок?

Ответ. Фермер привез на рынок 63 яблока.

Задача 28. Гусеница.

В 6 часов утра в воскресенье гусеница начала вползать на дерево. В течение всего дня, т. е. до 18 часов, она вползла на высоту 5 метров, а в течение ночи спустилась на 2 метра. В какой день и час она вползет на высоту 9 метров?

Ответ. На высоте 9 метров гусеница окажется во вторник в 13 часов 12 минут.

Задача 29. Бой часов.

Сколько ударов в сутки делают часы с боем?

Ответ. 156 ударов.

Задача 30. Странное число.

Некоторое число начинается на 1 и оканчивается на 2. Если эту его последнюю цифру переставить на первое место, то число удвоится. Какое это число? Расчет проведите до 15 цифр.

Ответ. 105 263 157 894 736 842.

Задача 31. Скворцы.

Скворцы расселись на деревьях. Когда они сели по одному на дерево, то одному скворцу не хватило дерева, а когда на каждое дерево сели по два скворца, то одно дерево осталось незанятым. Сколько было скворцов и сколько было деревьев?

Ответ. Скворцов было 4, деревьев – 3.

Задача 32. Рыбаки.

У двух рыбаков спросили: “Сколько рыбы в ваших корзинах?” “В моей корзине половина числа рыб, находящихся в корзине у него, да еще десять”, – ответил первый. “А у меня в корзине столько рыб, сколько у него, да еще двадцать”, – сказал второй. Сколько же рыб у каждого из рыбаков?

Ответ. У первого рыбака 40 рыб, у второго - 60.

Задача 33. Что это такое?

Две ноги сидели на трех, а когда пришли четыре и утащили одну, то две ноги, схватив три. бросили их в четыре, чтобы четыре оставили одну?

Ответ. Повар сидел на табурете, имеющем три ножки, пришла собака и утащила куриную ножку Повар бросил в собаку табурет, чтобы она оставила куриную ножку.

Задача 34. Разделите квас поровну.

Восьмиведерный бочонок заполнен доверху квасом. Двое должны разделить квас поровну. Но у них только два пустых бочонка, в один из которых входит 5 ведер, а в другой – 3 ведра. Как они могут разделить квас, пользуясь только этими тремя бочонками?

Сказка — ложь, да в ней намёк…

1.

Царь высказал некоторое утверждение, при этом он сказал правду. Потом Иванушка–дурачок дословно повторил это же утверждение, и оказалось, что при этом он солгал. Могло ли такое быть?

2.

У купца украли дорогой кафтан. Те, кто крадёт кафтаны, всегда лгут. Марфа сказала, что знает, кто украл кафтан. Виновна ли Марфа в краже?

3.

а)

Про Соловья–разбойника известно, что он всегда говорит неправду. Сможет ли он когда–нибудь в этом сознаться?

б)

Соловей–разбойник утверждает, что у него нет ни братьев, ни сестёр, но есть племянник. Какой вывод о составе семьи Соловья можно сделать из этих слов?

4.

Царь приказал отправить на поимку Соловья–разбойника богатырей числом не меньше тридцати. Однако потом царь подумал, что Соловей очень силён, поэтому приказал отправить против него богатырей числом не меньше тридцати трёх. Известно, что только один из приказов царя был исполнен. Сколько же богатырей могло отправиться на поимку Соловья?

5.

Добрыня Никитич, Илья Муромец и Алёша Попович пошли на Змея Горыныча, и один из них победил его. Когда они пришли к царю, и тот спросил их, кто победил Змея, каждый из богатырей указал на другого, при этом правду сказал только Добрыня Никитич. Если бы каждый из них указал не на того, на кого указывал, а на другого, то правду сказал бы только Алёша Попович. Так кто же победил Змея Горыныча?

6.

Иванушка–дурачок, Василиса Премудрая и Емеля считали ворон на дубах.

Иванушка: На первом дубе ворон больше 18. На втором — не больше 14.

Василиса: На первом дубе ворон меньше 20. На втором — 14.

Емеля: На первом дубе 17 ворон. На втором — больше 14.

Известно, что один (или одна?) из них оба раза ошибся (ошиблась?), а двое других оба раза были правы. Сколько ворон на каждом дубе?

7.

«У Василисы Премудрой больше 1000 книг», — сказал Добрыня. «Нет, книг у неё меньше 1000», — возразил Илья. «Одна–то книга у неё наверняка есть», — сказал Алёша. Сколько книг может быть у Василисы, если истинно только одно из этих утверждений? Укажите все возможные варианты!

8.

Илье Муромцу, Добрыне Никитичу и Алёше Поповичу за верную службу дали 6 монет: 3 золотых и 3 серебряных. Каждому досталось по две монеты. Илья Муромец не знает, какие монеты достались Добрыне, а какие Алёше, но знает, какие монеты достались ему самому. Придумайте вопрос, на который Илья Муромец ответит “да”, “нет” или “не знаю” и по ответу на который вы сможете понять, какие монеты ему достались.

9.

Двое из ларца одинаковы с лица: один — Пётр, другой — Павел. Один из них всегда говорит правду, а другой всегда лжёт. Вы можете задать только один вопрос одному из двоих, на который он ответит “да” или “нет”. Попробуйте выяснить, как зовут каждого из двоих.

Умей сказать «нет»

Отрицание к утверждению А — это такое утверждение Б, которое ПРОТИВОРЕЧИТ утверждению А, но которое ВЕРНО ВСЕГДА, КОГДА УТВЕРЖДЕНИЕ А НЕВЕРНО.

Постройте отрицания к следующим утверждениям (9.1–9.11).

1.

На Марсе есть жизнь.

2.

Сегодня не холодно.

3.

Снежинки падают с неба.

4.

Все птицы летают.

5.

Не каждая птица долетит до середины Днепра.

6.

Некоторые школьники лицея едят чипсы во время перемен.

7.

Любому преподавателю Лицея не менее 18 лет.

8.

В этом листочке нет ни одной трудной задачи.

9.

Стены Кремля жёлтые или зелёные.

10.

Кролик Дуся белый и пушистый.

11.

У Николая нет ни ручки, ни карандаша, но есть ластик.

12.

Контрольную работу назовём лёгкой, если за любой партой есть ученик, решивший её хотя бы наполовину, и к тому же не менее половины класса решило её полностью. Дайте определение сложной контрольной работы (то есть такой, которая не является лёгкой).

13.

Двух пятиклассников и двух шестиклассников из одной школы спросили: «Кто в вашей школе выше: пятиклассники или шестиклассники?» Прозвучали следующие ответы:

Любой шестиклассник выше некоторого пятиклассника.

Один из шестиклассников выше одного из пятиклассника.

Любой шестиклассник выше любого пятиклассника.

Один из шестиклассников выше любого пятиклассника.

После этого шестиклассники признались, что пошутили, а пятиклассники подтвердили, что отвечали честно. Можно ли определить, верно ли:

а)

первое утверждение;

б)

второе утверждение;

в)

третье утверждение;

г)

четвёртое утверждение?

Круги Эйлера

1.

В классе все увлекаются математикой или биологией. Сколько человек в классе, если математикой увлекаются 15 человек, биологией — 20, а математикой и биологией одновременно — 10?

2.

В классе 35 учеников. Из них 20 занимаются в математическом кружке, 11 — в биологическом, 10 ребят не посещают эти кружки. Сколько биологов увлекается математикой?

3.

рисунокНа стол бросили две квадратные салфетки 5 × 5 см, как показано на рисунке справа. Они покрыли площадь стола, равную 43 см2. Какова площадь их перекрытия?

4.

В классе послушных девочек столько же, сколько непослушных мальчиков. Кого в классе больше: мальчиков или послушных детей?

5.

У Пети есть карточки, у которых каждая сторона — красная или синяя. Карточек с синей стороной — 10, карточек с красной стороной — 12, карточек с разными сторонами — 5. Сколько карточек, у которых стороны одного цвета?

6.

На прогулку пошли шестиклассники и пятиклассники. Все они были либо босиком, либо в тапочках. Шестиклассников было 24, а босых учеников 16. Обутых пятиклассников было столько же, сколько босых шестиклассников. Сколько учеников ходили на прогулку?

7.

Кто–то в классе любит математику, кто–то — литературу, а кто–то — и то, и другое. За сентябрь–октябрь число любителей математики и число любителей литературы не изменились, а вот тех, кто любит оба предмета, стало меньше на 5 человек. Как изменилось число тех, кто не любит ни математику, ни литературу?

8.

На олимпиаде было предложено две задачи. После проверки жюри составило четыре списка. В первый список внесли решивших первую задачу (включая и тех, кто решил обе задачи), во второй — решивших только одну задачу, а в третий — решивших по меньшей мере одну задачу. Четвёртый же список состоял из решивших обе задачи.

а)

Какой из списков самый длинный?

б)

Могут ли какие–то три списка совпадать по составу? Если да, то какие? А все четыре — могут?

9.

Стёпа Мошкин рассказывал своему другу из соседней школы Васе Комарову: «У нас в классе работает три спортивных секции. В лыжной секции занимаются 22 человека, в секции плавания — 9 человек, а в велосипедной секции — 11 человек, причём каждый спортсмен занимается в двух секциях». «Ты что–то путаешь, — прервал его рассказ Вася, — такого быть не может, так как…» Что дальше сказал Вася Стёпе?

Примерная контрольная работа(итоговая)

1. Встретились два жителя острова рыцарей и лжецов. Один из них сказал: «По крайней мере один из нас — рыцарь». Второй ему ответил: «Ты — лжец». Кто из них кто на самом деле?

2.Какие 500 идущих подряд натуральных чисел надо выписать, чтобы всего было выписано 2015 цифр?

3.Хулиган Гоша порвал школьную стенгазету на 3 части. После этого он взял одну из частей и тоже порвал на 3 части. Потом он опять порвал одну из частей на 3 части, и так далее. Могло ли у него получиться 100 частей за несколько таких операций? А 2015 частей?

4.У Пети в кармане могут быть монеты в 1 руб., 2 руб., 5 руб. и 10 руб.

а)В кармане 10 монет, и если Петя наугад вытащит из кармана 3 монеты, среди них обязательно найдётся монета в 1 рубль. Какая наибольшая сумма денег может быть в кармане?

б)В кармане 10 монет, и если Петя наугад вытащит из кармана 7 монет, среди них обязательно найдутся три монеты разного достоинства. Какая наибольшая сумма денег может быть в кармане?

в)Если Петя наугад вытащит из кармана 3 монеты, среди них обязательно найдётся монета в 1 рубль. Если Петя наугад вытащит из кармана 4 монеты, среди них обязательно найдётся монета в 2 рубля. Петя вытащил из кармана 5 монет. Назовите эти монеты.

5.На каждой перемене Робин–Бобин–Барабек съедает по конфете. За неделю (с понедельника по субботу) было 30 уроков. Сколько всего конфет съел Робин? (Каждый день был хотя бы один урок.)

6.У Олега есть коробка такой формы, как левый треугольник на рисунке, и кусок торта такой формы, как правый треугольник на рисунке.

а)Как ему разрезать кусок торта на две части, чтобы уложить его в коробку?

б)Как ему разрезать кусок торта на три части, чтобы уложить его в квадратную коробку 3×3 клетки?рисунок

7.В парламенте острова рыцарей и лжецов заседает 101 депутат. В целях сокращения бюджета руководство острова решило уменьшить состав парламента на одного человека. Но каждый из депутатов сказал, что если его исключат из парламента, то среди оставшихся депутатов большинство будут лжецами. Сколько лжецов и рыцарей было в парламенте изначально?

8.Прямоугольник 5×9 разрезали по клеточкам на 10 прямоугольников. Докажите, что среди них обязательно найдутся два одинаковых.

копилка материалов

http://mmmf.msu.ru/archive/20152016/z5/