Рабочая программа по алгебре 9 класс Мерзляк А.Г.

Раздел I. Пояснительная записка.

1. Рабочая программа по алгебре для 9 класса составлена на основе

авторской программы предметной линии системы УМК «Алгоритм успеха» по алгебре 7-9 классов А.Г. Мерзляк, В.Б. Полонский, М.С. Якир, в соответствии с требованиями к результатам освоения основной образовательной программы МКОУ «Ягульская СОШ имени Героя Советского Союза Ф.М.Дербушева» и направлена на достижение учащимися личностных, метапредметных и предметных результатов по алгебре.

2. Используемый УМК включает: учебник для общеобразовательных классов Алгебра. 9 класс. А.Г. Мерзляк, В.Б. Полонский, М.С. Якир . – М.: Вентана-Граф, 2018, дидактические материалы, А.Г. Мерзляк, В.Б. Полонский, Е.М.Рабинович, М.С. Якир .

3. Учебный план МКОУ «Ягульская СОШ имени Героя Советского Союза Ф.М.Дербушева» предусматривает в 9 классе изучение алгебры в объеме 102 часа в год, 3 часа в неделю.

Предмет «Алгебра» относится к предметной области Математика и информатика. Для обязательного изучения учебного предмета «Математика» в 9 классе отводится 3 часа в неделю, в 2020-2021 учебном году предусматривается 34 учебные недели, что соответствует общему количеству 102 часов в 9 классе.

Цели обучения

Обучение алгебре в основной школе направлено на достижение следующих целей:

1. В направлении личностного развития:

• развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;

• формирование у учащихся интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;

• воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;

• формирование качеств мышления, необходимых для адаптации в современном информационном обществе;

• развитие интереса к математическому творчеству и математических способностей.

2. В метапредметном направлении:

• формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;

• развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;

• формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности.

3. В предметном направлении:

• овладение математическими знаниями и умениями, необходимыми для продолжения обучения в старшей школе или иных общеобразовательных учреждениях, изучения смежных дисциплин, применения в повседневной жизни;

• создание фундамента для математического развития, формирования механизмов мышления, характерных для математической деятельности.

Раздел II. Содержание курса алгебры 9 класса

1. Неравенства.

Числовые неравенства и их свойства. Почленное сложение и умножение числовых неравенств. Линейные неравенства с одной переменной и их сис­темы.

Основная цель — ознакомить учащихся с применение: неравенств для оценки значений выражений, выработать умение решать линейные неравенства с одной переменной и их системы. Свойства числовых неравенств составляют ту базу, на которой основано решение линейных неравенств с одной переменной. Теоремы о почленном сложении и умножении неравенств, находить применение при выполнении простейших упражнений на оценку выражений по методу границ. Вводятся понятия абсолютной погрешности и точности приближения, относительной погрешности. Умения проводить дедуктивные рассуждения получают развитие как при доказательствах указанных теорем, так и при выполнении упражнений на доказательства неравенств.

В связи с решением линейных неравенств с одной переменно: дается понятие о числовых промежутках, вводятся соответствующие названия и обозначения. Рассмотрению систем неравенств одной переменной предшествует ознакомление учащихся с понятиями пересечения и объединения множеств.

При решении неравенств используются свойства равносильных неравенств, которые разъясняются на конкретных примерах. Особое внимание следует уделить отработке умения решат простейшие неравенства вида ахb, ахb, остановившись специально на случае, когда а 0.

В этой теме рассматривается также решение систем двух линейных неравенств с одной переменной, в частности таких, которые записаны в виде двойных неравенств.

1. Квадратичная функция.

Функция. Свойства функций. Квадратный трехчлен. Разложение квадратного трехчлена на множители. Функция у = aх² + bх + с, ее свойства и график. Степенная функция.

Основная цель — расширить сведения о свойствах функций, ознакомить учащихся со свойствами и графиком квадратичной функции. I

В начале темы систематизируются сведения о функциях. Повторяются основные понятия: функция, аргумент, область опре­деления функции, график. Даются понятия о возрастании и убы­вании функции, промежутках знакопостоянства. Тем самым создается база для усвоения свойств квадратичной и степенной функций, а также для дальнейшего углубления функциональных представлений при изучении курса алгебры и начал анализа.

Подготовительным шагом к изучению свойств квадратичной функции является также рассмотрение вопроса о квадратном трехчлене и его корнях, выделении квадрата двучлена из квадратного трехчлена, разложении квадратного трехчлена на множители.

Изучение квадратичной функции начинается с рассмотрения функции у = ах², ее свойств и особенностей графика, а также других частных видов квадратичной функции — функций у = ах² + b, у = а (х - m)². Эти сведения используются при изучении свойств квадратичной функции общего вида. Важно, чтобы учащиеся поняли, что график функции у = ах² + bх + с может быть получен из графика функции у = ах² с помощью двух па­раллельных переносов. Приемы построения графика функции y = ах² + bх + с отрабатываются на конкретных примерах. При этом особое внимание следует уделить формированию у учащих­ся умения указывать координаты вершины параболы, ее ось симметрии, направление ветвей параболы.

При изучении этой темы дальнейшее развитие получает умение находить по графику промежутки возрастания и убывания функ­ции, а также промежутки, в которых функция сохраняет знак.

Учащиеся знакомятся со свойствами степенной функции у = х^п при четном и нечетном натуральном показателе п. Вводит­ся понятие корня n-й степени. Они получают представление о нахождении значений корня с помощью калькулятора, причем выработка соответствующих умений не требуется.

1. Неравенства с одной переменной

Целые уравнения. Дробные рациональные уравнения. Нера­венства второй степени с одной переменной. Метод интервалов.

Основная цель — систематизировать и обобщить сведе­ния о решении целых и дробных рациональных уравнений с од­ной переменной, сформировать умение решать неравенства вида ах² + bх + с 0 или ах² + bх + с 0, где а ≠ 0.

В этой теме завершается изучение рациональных уравнений с одной переменной. В связи с этим проводится некоторое обобще­ние и углубление сведений об уравнениях. Вводятся понятия це­лого рационального уравнения и его степени. Учащиеся знако­мятся с решением уравнений третьей степени и четвертой степени с помощью разложения на множители и введения вспо­могательной переменной. Метод решения уравнений путем введе­ния вспомогательных переменных будет широко использоваться в дальнейшем при решении тригонометрических, логарифмиче­ских и других видов уравнений.

Расширяются сведения о решении дробных рациональных уравнений. Учащиеся знакомятся с некоторыми специальными приемами решения таких уравнений.

Формирование умений решать неравенства вида ах² + bх + + с 0 или ах² + bх + сО, где а ≠ 0 , осуществляется с опорой на сведения о графике квадратичной функции.

Учащиеся знакомятся с методом интервалов, с помощью ко­торого решаются несложные рациональные неравенства.

1. Неравенства с двумя переменными

Уравнение с двумя переменными и его график. Системы урав­нений второй степени. Решение задач с помощью систем уравнений второй степени. Неравенства с двумя переменными и их системы.

Основная цель — выработать умение решать простейшие системы, содержащие уравнение второй степени с двумя перемен­ными, и текстовые задачи с помощью составления таких систем.

В данной теме завершается изучение систем уравнений с дву­мя переменными. Основное внимание уделяется системам, в ко­торых одно из уравнений первой степени, а другое второй.

Из­вестный учащимся способ подстановки находит здесь дальнейшее применение и позволяет сводить решение таких систем к решению квадратного уравнения.

Ознакомление учащихся с примерами систем уравнений с двумя переменными, в которых оба уравнения второй степени, должно осуществляться с достаточной осторожностью и ограничиваться простейшими примерами.

Привлечение известных учащимся графиков позволяет привести примеры графического решения систем уравнений. С помо­щью графических представлений можно наглядно показать учащимся, что системы двух уравнений с двумя переменными: второй степени могут иметь одно, два, три, четыре решения или не иметь решений.

Разработанный математический аппарат позволяет существенно расширить класс содержательных текстовых задач, решаемых с помощью систем уравнений.

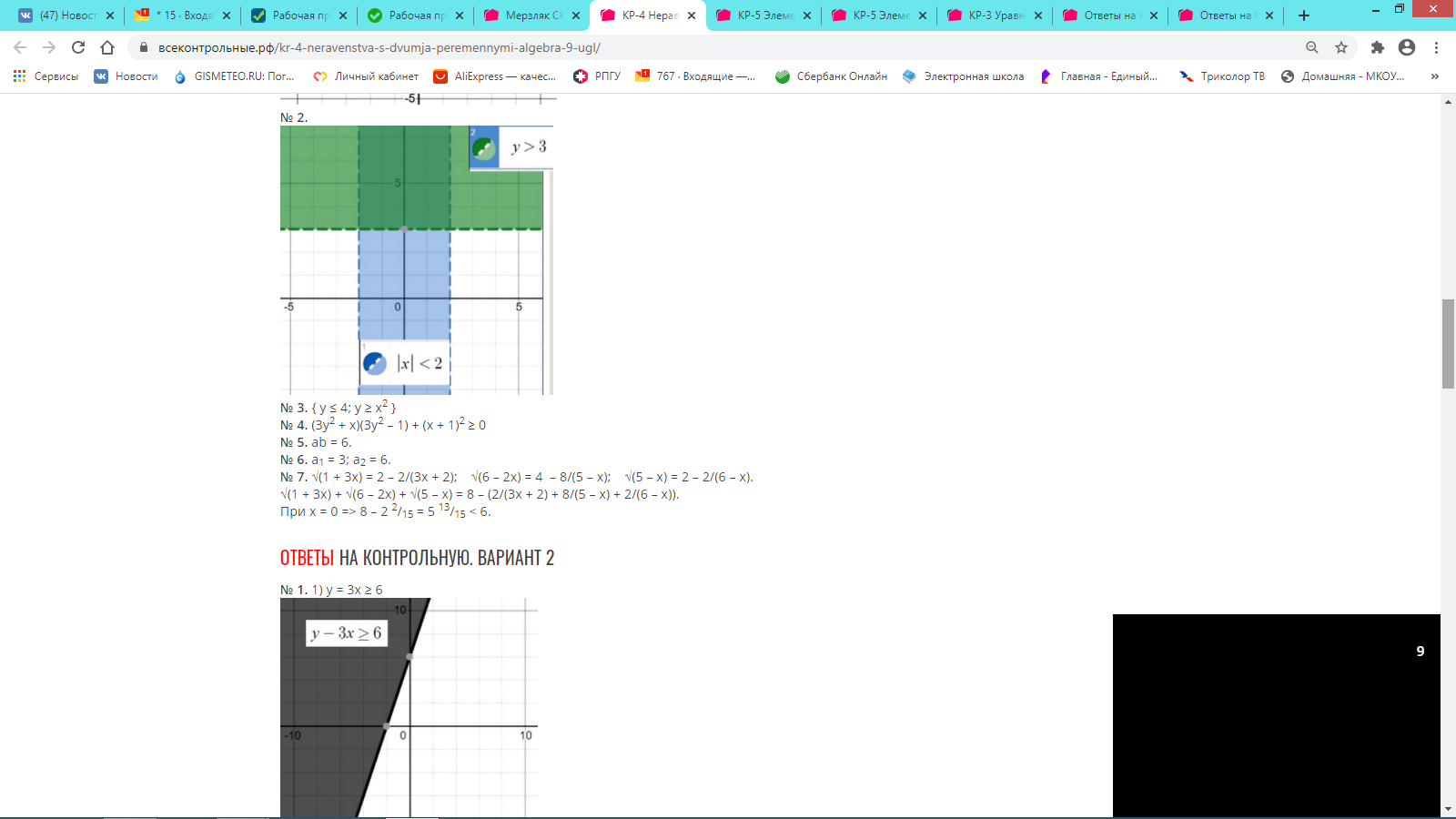
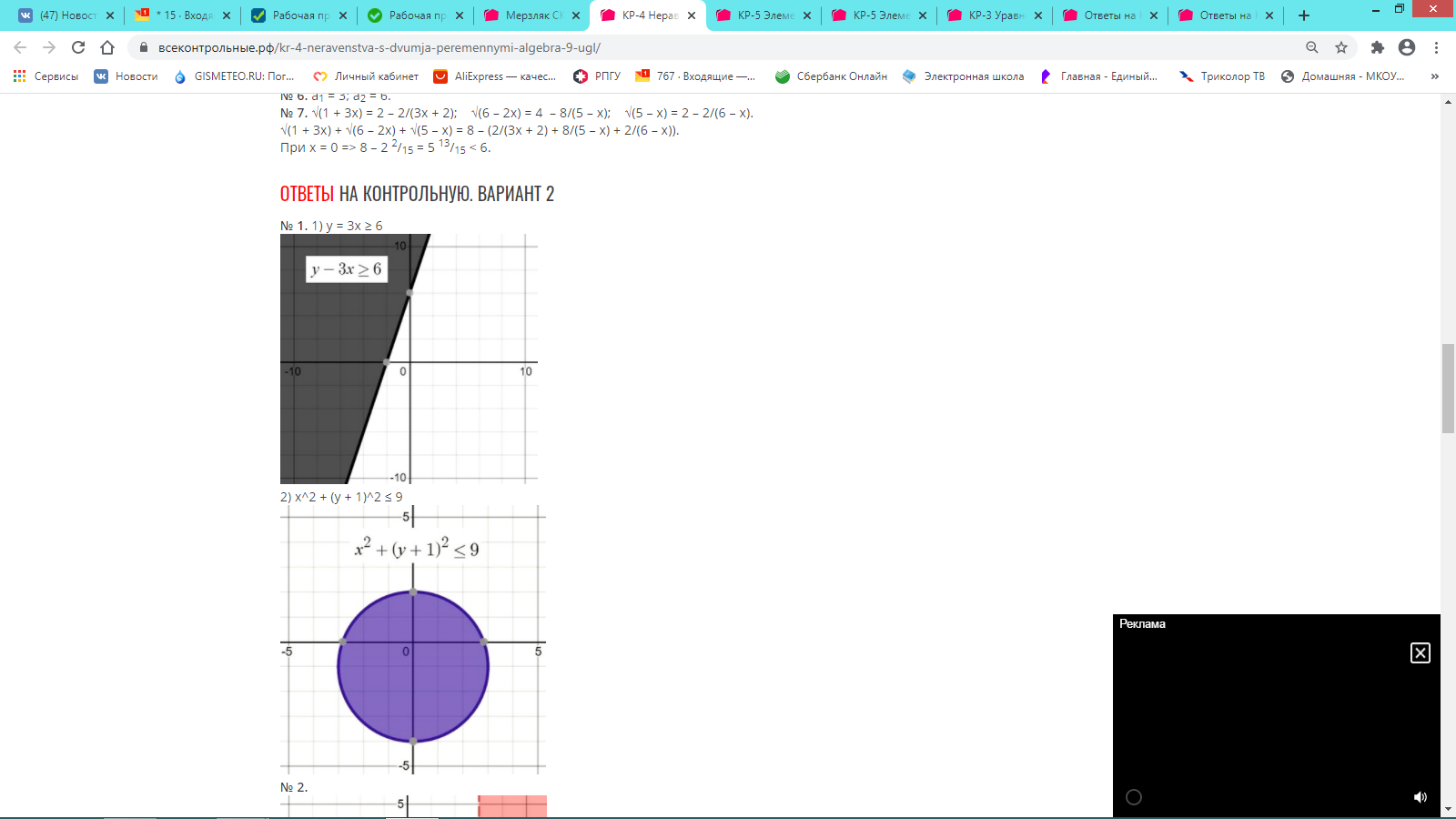
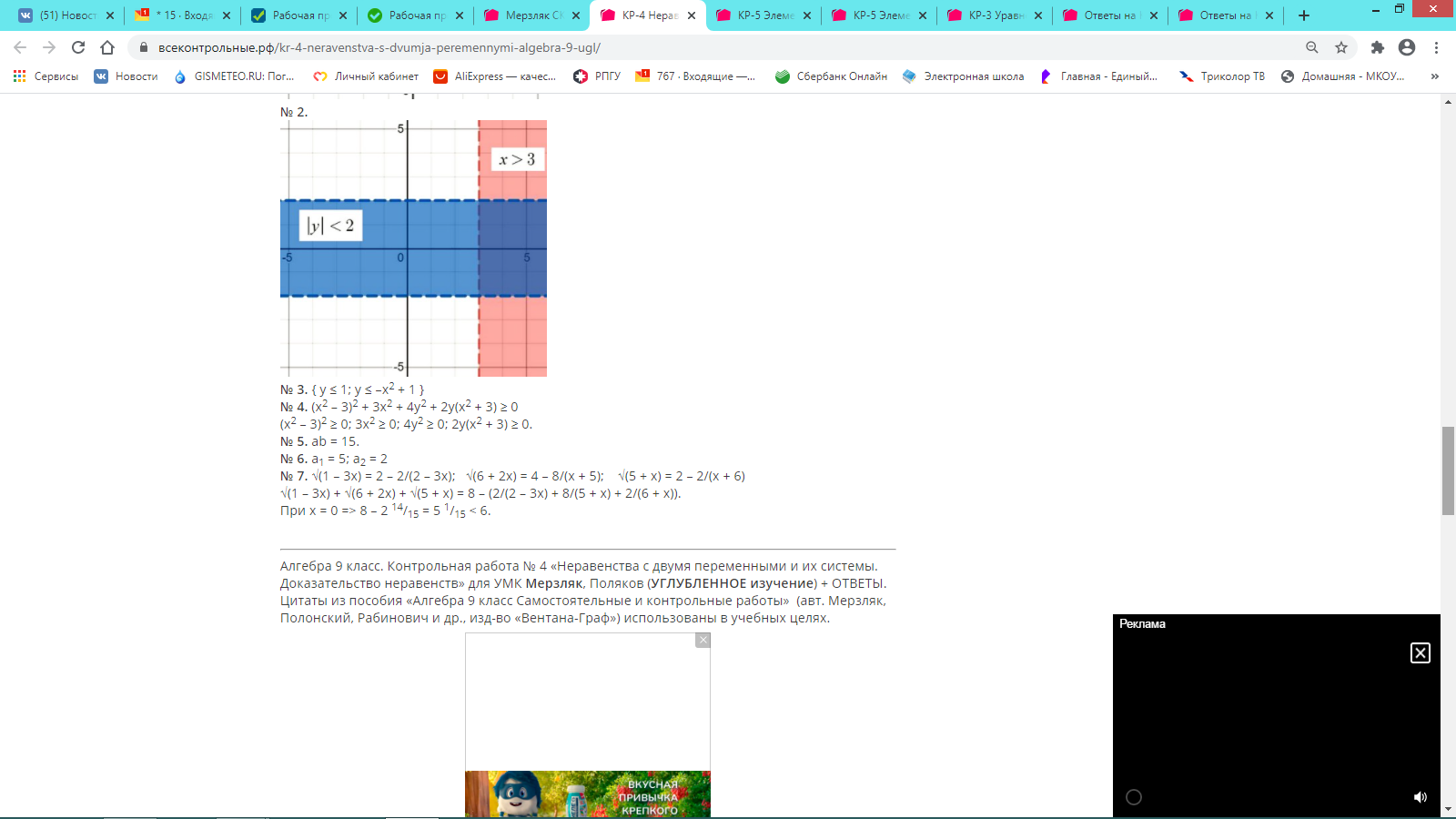
Изучение темы завершается введением понятий неравенства двумя переменными и системы неравенств с двумя переменными. Сведения о графиках уравнений с двумя переменными используются при иллюстрации множеств решений некоторых простейших неравенств с двумя переменными и их систем.

1. Элементы прикладной математики.

Математическое моделирование. Процентные расчеты. Приближенные вычисления. Основные правила комбинаторики. Относительная частота и вероятность случайного события. Классическое определение вероятности. Начальные сведения о статистике.

Основная цель — ознакомить учащихся с понятиями пе­рестановки, размещения, сочетания и соответствующими форму­лами для подсчета их числа; ввести понятия относительной час­тоты и вероятности случайного события.

Изучение темы начинается с решения задач, в которых требу­ется составить те или иные комбинации элементов и подсчитать их число. Разъясняется комбинаторное правило умножения, ко­торое используется в дальнейшем при выводе формул для подсче­та числа перестановок, размещений и сочетаний. При изучении данного материала необходимо обратить внима­ние учащихся на различие понятий «размещение» и «сочета­ние», сформировать у них умение определять, о каком виде ком­бинаций идет речь в задаче.

В данной теме учащиеся знакомятся с начальными сведениями из теории вероятностей. Вводится понятие «случайное собы­тие», «относительная частота», «вероятность случайного собы­тия». Рассматриваются статистический и классический подходы к определению вероятности случайного события. Важно обратить внимание учащихся на то, что классическое определение вероят­ности можно применять только к таким моделям реальных собы­тий, в которых все исходы являются равновозможными.

1. Числовые последовательности.

Числовые последовательности. Арифметическая и геометрическая прогрессии. Формулы п-гочлена и суммы первых n членов прогрессии. Бесконечно убывающая геометрическая прогрессия.

Основная цель — дать понятия об арифметической и геометрической прогрессиях как числовых последовательностях особого вида.

При изучении темы вводится понятие последовательности, разъясняется смысл термина «n-й член последовательности», вырабатывается умение использовать индексное обозначение. Эти сведения носят вспомогательный характер и используются для изучения арифметической и геометрической прогрессий.

Работа с формулами n-го члена и суммы первых га членов прогрессий, помимо своего основного назначения, позволяет неоднократно возвращаться к вычислениям, тождественным преобразованиям, решению уравнений, неравенств, систем.

Рассматриваются характеристические свойства арифметической и геометрической прогрессий, что позволяет расширить круг предлагаемых задач.

7. Алгебра в историческом развитии

Зарождение алгебры, книга о восстановлении и противопоставлении Мухаммеда аль-Хорезми. История формирования математического языка. История развития понятия функции.

Л.Ф. Магницкий. П.Л. Чебышев. Н.И. Лобачевский. В.Я. Буняковский. А.Н. Колмогоров. Ф. Виет. П. Ферма. Р. Декарт. Н. Тарталья. Д. Кардано. Н. Абель. Б. Паскаль. Л. Пизанский. К. Гаусс.

1. Повторение (итоговое)

Основная цель. Повторить, закрепить и обобщить основные ЗУН, полученные в 9 классе.

Раздел III. Личностные, предметные, метапредметные результаты учебного предмета

Изучение алгебры в 9-ом классе основной школы дает возможность обучающимся достичь следующих результатов развития:

в личностном направлении:

1. воспитание российской гражданской идентичности: патриотизма, уважения к Отечеству, осознания вклада отечественных учёных в развитие мировой науки;

2. ответственное отношение к учению, готовность и способность обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию;

3. осознанный выбор и построение дальнейшей индивидуальной траектории образования на базе ориентировки в мире профессий и профессиональных предпочтений с учётом устойчивых познавательных интересов, а также на основе формирования уважительного отношения к труду, развитие опыта участия в социально значимом труде;

4. умение контролировать процесс и результат учебной и математической деятельности;

5. критичность мышления, инициатива, находчивость, активность при решении математических задач.

в метапредметном направлении:

1. умение самостоятельно определять цели своего обучения, ставить и формулировать для себя новые задачи

   • учёбе:

• развивать мотивы и интересы своей познавательной деятельности;

• умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности

• процессе достижения результата:

• определять способы действий в рамках предложенных условий и требований;

• корректировать свои действия в соответствии с изменяющейся ситуацией;

1. умение определять понятия, создавать обобщения, устанавливать аналогии, классифицировать, самостоятельно выбирать основания и критерии для классификации;

2. умение устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и делать выводы;

3. развитие компетентности в области использования информационно-коммуникационных технологий;

4. первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;

5. умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни; умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять её в понятной форме, принимать решение в условиях неполной или избыточной, точной или вероятностной информации;

1. умение понимать и использовать математические средства наглядности (графики, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации;

1. умение выдвигать гипотезы при решении задачи, понимать необходимость их проверки;

2. понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом.

в предметном направлении:

1) осознание значения математики в повседневной жизни человека;

2) представление о математической науке как сфере математической деятельности, об этапах её развития, о её значимости для развития цивилизации

3) развитие умение работать с учебным математическим текстом ( анализировать извлекать необходимую информацию), точно и грамотно излагать свои мысли с применением математической терминологии и символики, проводить классификацию, логические обоснования;

4) владение базовым понятийным аппаратом по основным разделам содержания;

5) систематические знания о функциях и их свойствах;

6) практически значимые математические умения и навыки, их применение к решению математических и нематематических задач, предполагающее умения:

• выполнять вычисления с действительными числами;

• решать текстовые задачи с помощью уравнений и систем уравнений;

• использовать алгебраический язык для описания предметов окружающего мира и создания соответствующих математических моделей;

• выполнять тождественные преобразования алгебраических выражений;.

• исследовать линейные функции и строить их графики.

Раздел IV. Ожидаемые результаты

В результате изучения математики ученик научится понимать:

- существо понятия математического доказательства; примеры доказательств;

- существо понятия алгоритма; примеры алгоритмов;

- как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;

- как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;

- как потребности практики привели математическую науку к необходимости расширения понятия числа;

-вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;

- смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации; владеть компетенциями: познавательной, коммуникативной, информационной и рефлексивной;

уметь:

- составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;

- выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;

- применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;

- решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним;

- решать линейные неравенства с одной переменной и их системы;

- решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;

- изображать числа точками на координатной прямой;

- находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;

- определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;

- описывать свойства изученных функций, строить их графики;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

- выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;

- моделирования практических ситуаций и исследования построенных моделей с использованием аппарата алгебры;

- описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;

- интерпретации графиков реальных зависимостей между величинами.

Раздел V. Тематическое планирование

№ урока	Содержание (разделы, темы)	Кол-во часов
1	Повторение «Преобразование рациональных выражений»	1
2	Преобразование выражений, содержащих квадратные корни	1
3	Решение квадратных уравнений	1
4	Входная контрольная работа	1
	Глава 1 «Неравенства№
5	Числовые неравенства	1
6	Сравнение значений выражений	1
7	Доказательство неравенств	1
8	Основные свойства числовых неравенств.	1
9	Применение основных свойств числовых неравенств	1
10	Сложение и умножение числовых неравенств	1
11	Отработка навыков сложения и умножения числовых неравенств. Самостоятельная работа	1
12	Оценивание значений выражений	1
13	Неравенства с одной переменной	1
14	Числовые промежутки	1
15	Неравенства с одной переменной Числовые промежутки. Самостоятельная работа	1
16	Наибольшее и наименьшее целое значение неравенств	1
17	Задания с параметрами	1
18	Отработка навыков решения неравенств с одной переменной	1
19	Системы линейных неравенств с одной переменной	1
20	Решение систем неравенств с одной переменной	1
21	Решение двойных неравенств	1
22	Решение неравенств с модулем.	1
23	Отработка навыков решения систем неравенств с одной переменной.	1
24	Контрольная работа №1 по теме «Неравенства»	1
	Глава II «Квадратичная функция»
25	Повторение и расширение сведений о функции	1
26	Область определения функции и множество значений функции	1
27	Способы задания функции.	1
28	Свойства функции	1
29	Исследование функции на монотонность	1
30	Графики кусочных функций.	1
31	Как построить график функции y = kf(x), если известен график функции y = f(x)	1
32	Построение графика функции y = kf(x), если известен график функции y = f(x)	1
33	Как построить график функции y = f(x) + b, известен график функции y = f(x)	1
34	Отработка навыков построения графиков функций y = f(x) + b, известен график функции y = f(x)	1
35	Как построить график функции y = f(x + a), если известен график функции y = f(x)	1
36	Отработка навыков построения графиков функций y = f(x + a), если известен график функции y = f(x)	1
37	Квадратичная функция.	1
38	График квадратичной функции.	1
39	Свойства квадратичной функции.	1
40	Отработка навыков построения графиков квадратичной функции. Самостоятельная работа.	1
41	Графическое решение уравнений.	1
42	Применение графиков квадратичной функции при решении заданий с параметрами.	1
43	Контрольная работа № 2 по теме «Квадратичная функция»	1
44	Квадратные неравенства.	1
45	Решение квадратных неравенств.	1
46	Нахождение множества решений неравенства	1
47	Метод интервалов	1
48	Нахождение области определения выражения и функции	1
49	Отработка навыков решения квадратных неравенств.	1
50	Системы уравнений с двумя переменными	1
51	Графический метод решения систем с двумя переменными	1
52	Метод подстановки решения систем с двумя переменными	1
53	Метод сложения решения систем с двумя переменными	1
54	Метод замены переменных решения систем с двумя переменными	1
55	Решения систем с двумя переменными различными способами. Самостоятельная работа.	1
56	Решение задач с помощью систем уравнений второй степени	1
57	Отработка навыков решения задач с помощью систем уравнений второй степени.	1
58	Контрольная работа № 3 по теме «Квадратные неравенства»	1
	Глава III.Элементы прикладной математики
59	Математическое моделирование	1
60	Задачи на движение	1
61	Задачи на работу	1
62	Процентные расчёты	1
63	Три основные задачи на проценты	1
64	Простые и сложные проценты	1
65	Приближённые вычисления	1
66	Абсолютная и относительная погрешность	1
67	Основные правила комбинаторики	1
68	Правило суммы и произведения	1
69	Отработка навыков применения правил суммы и произведения	1
70	Случайные достоверные и невозможные события	1
71	Частота и вероятность случайного события	1
72	Классическое определение вероятности	1
73	Решение вероятностных задач.	1
74	Решение вероятностных задач. Самостоятельная работа	1
75	Начальные сведения о статистике	1
76	Способы представления данных	1
77	Основные статистические характеристики	1
78	Контрольная работа № 4 по теме «Элементы прикладной математики»	1
	Глава 4 Числовые последовательности
79	Числовая последовательность. Аналитический способ задания последовательности	1
80	Словесный и рекуррентный способы задания функции.	1
81	Арифметическая прогрессия. Формула n-го члена.	1
82	Решение задач на применение формулы n-го члена арифметической прогрессии.	1
83	Характеристическое свойство.	1
84	Решение задач по теме: «Арифметическая прогрессия». Самостоятельная работа.	1
85	Формула суммы членов конечной арифметической прогрессии.	1
86	Решение задач на нахождение суммы членов конечной арифметической прогрессии	1
87	Решение задач по теме: «Арифметическая прогрессия» Самостоятельная работа.	1
88	Геометрическая прогрессия. Формула n-го члена.	1
89	Решение задач на применение формулы n-го члена геометрической прогрессии	1
90	Решение задач на применение формулы n-го члена геометрической прогрессии. Самостоятельная работа.	1
91	Формула суммы членов конечной геометрической прогрессии	1
92	Решение задач на нахождение суммы членов конечной геометрической прогрессии. Характеристическое свойство.	1
93	Сумма бесконечной геометрической прогрессии, у которой | q |	1
94	Решение задач на нахождение суммы бесконечной геометрической прогрессии	1
95	Контрольная работа № 5 по теме «Числовые последовательности»	1
96	Повторение и систематизация учебного материала Числовые и алгебраические выражения	1
97	Уравнения(линейные, квадратные, дробно-рациональные). Системы уравнений	1
98	Неравенства(линейные, квадратные, дробно-рациональные). Системы неравенств	1
99	Задачи на составление уравнений	1
100	Решение задач по всему курсу «Алгебра 9».	1
101	Итоговая контрольная работа(промежуточная аттестация)
102	Итоговый урок

Раздел V. Планирование практической части

.

Вид	Тема	Дата
Контрольная работа №1	«Неравенства»
Контрольная работа №2	«Квадратичная функция»
Контрольная работа №3	«Квадратные неравенства»
Контрольная работа №4	«Элементы прикладной математики»
Контрольная работа №5	«Числовые последовательности»
Итоговая контрольная работа(промежуточная аттестация)

Раздел VII

Критерии оценивания образовательных результатов

ОЦЕНКА УСТНЫХ ОТВЕТОВ ОБУЧАЮЩИХСЯ ПО МАТЕМАТИКЕ

 Ответ оценивается отметкой «5», если ученик:

• полно раскрыл содержание материала в объеме, предусмотрен­ном программой и учебником;

• изложил материал грамотным языком в определенной логиче­ской последовательности, точно используя математическую термино­логию и символику;

• правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;

• показал умение иллюстрировать теоретические положения конк­ретными примерами, применять их в новой ситуации при выполне­нии практического задания;

• продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность и устойчивость используемых при от­работке умений и навыков;

• отвечал самостоятельно без наводящих вопросов учителя. Возможны одна - две неточности при освещении второстепенных вопросов или в выкладках, которые ученик легко исправил по замечанию учителя.

Ответ оценивается отметкой «4», если он удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:

• в изложении допущены небольшие пробелы, не исказившие математическое содержание ответа;

• допущены один – два недочета при освещении основного содержания ответа, исправленные по замечанию учителя;

• допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные по замечанию учителя.

 Отметка «3» ставится в следующих случаях:

• неполно или непоследовательно раскрыто содержание материала, но показано общее понимание вопроса и продемонстрированы умения, достаточные для дальнейшего усвоения программного материала (определенные «Требованиями к математической подготовке обучающихся»);

• имелись затруднения или допущены ошибки в определении понятий, использовании математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;

• ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;

• при знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.

 Отметка «2» ставится в следующих случаях:

• не раскрыто основное содержание учебного материала;

• обнаружено незнание или непонимание учеником большей или наиболее важной части учебного материала;

• допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

 

 

ОЦЕНКА ПИСЬМЕННЫХ КОНТРОЛЬНЫХ РАБОТ ОБУЧАЮЩИХСЯ ПО МАТЕМАТИКЕ

Отметка «5» ставится, если:

• работа выполнена полностью;

• в логических  рассуждениях и обосновании решения нет пробелов и ошибок; 

• в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием незнания или непо­нимания учебного материала).

Отметка «4» ставится, если:

• работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);

• допущена одна ошибка или два-три недочета в выкладках, ри­сунках, чертежах или графиках (если эти виды работы не являлись специальным объектом проверки).

 Отметка «3» ставится, если:

• допущены более одной ошибки или более двух-трех недоче­тов в выкладках, чертежах или графиках, но учащийся владеет обязательными умениями по проверяемой теме.

 Отметка «2» ставится, если:

• допущены существенные ошибки, показавшие, что учащийся не владеет обязательными умениями по данной теме в полной мере.

ОБЩАЯ КЛАССИФИКАЦИЯ ОШИБОК

Грубыми считаются ошибки:

• незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;

• незнание наименований единиц измерения;

• неумение выделить в ответе главное;

• неумение применять знания, алгоритмы для решения задач;

• неумение делать выводы и обобщения;

• неумение читать и строить графики;

• потеря корня или сохранение постороннего корня;

• отбрасывание без объяснений одного из них;

• равнозначные им ошибки;

• вычислительные ошибки, если они не являются опиской;

• логические ошибки.

 К негрубым ошибкам следует отнести:

• неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;

• неточность графика;

• нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);

• нерациональные методы работы со справочной и другой литературой;

• неумение решать задачи, выполнять задания в общем виде.

Недочетами являются:

• нерациональные приемы вычислений и преобразований;

• небрежное выполнение записей, чертежей, схем, графиков.

Раздел VIII. Лист внесения изменений и дополнений в рабочую программу

№ п/п	Тема урока	Дата по плану	Причина корректировки	Корректирующие мероприятие	Новая тема	Дата проведения	Реквизиты приказа

Раздел IX. Литература

Учебно-методическое и материально техническое обеспечение образовательного процесса

Мерзляк А.Г. Математика: программы: 5 – 9 классы / А.Г. Мерзляк, В.Б.Полонский, М.С. Якир, Е.В.Буцко. – М: Вентана_граф, 2013.

Мерзляк А.Г. Алгебра: 9 класс: учебник для учащихся общеобразовательных организаций / А.Г.Мерзляк, В.Б. Полонский, М.С. Якир – М: Вентана-Граф, 2014 – 2017.

Мерзляк А.Г. Алгебра: дидактические материалы: 9 класс: пособие для учащихся общеобразовательных организаций / А.Г. Мерзляк, В.Б.Полонский, Е.М. Рабинович и др. – М: Вентана-Граф, 2016.

Буцко Е.В. Алгебра: 9 класс: методическое пособие / Е.В. Буцко, А.Г. Мерзляк, В.Б.Полонский, М.С. Якир – М: Вентана-Граф, 2016.

Раздел X. Контрольно-измерительные материалы

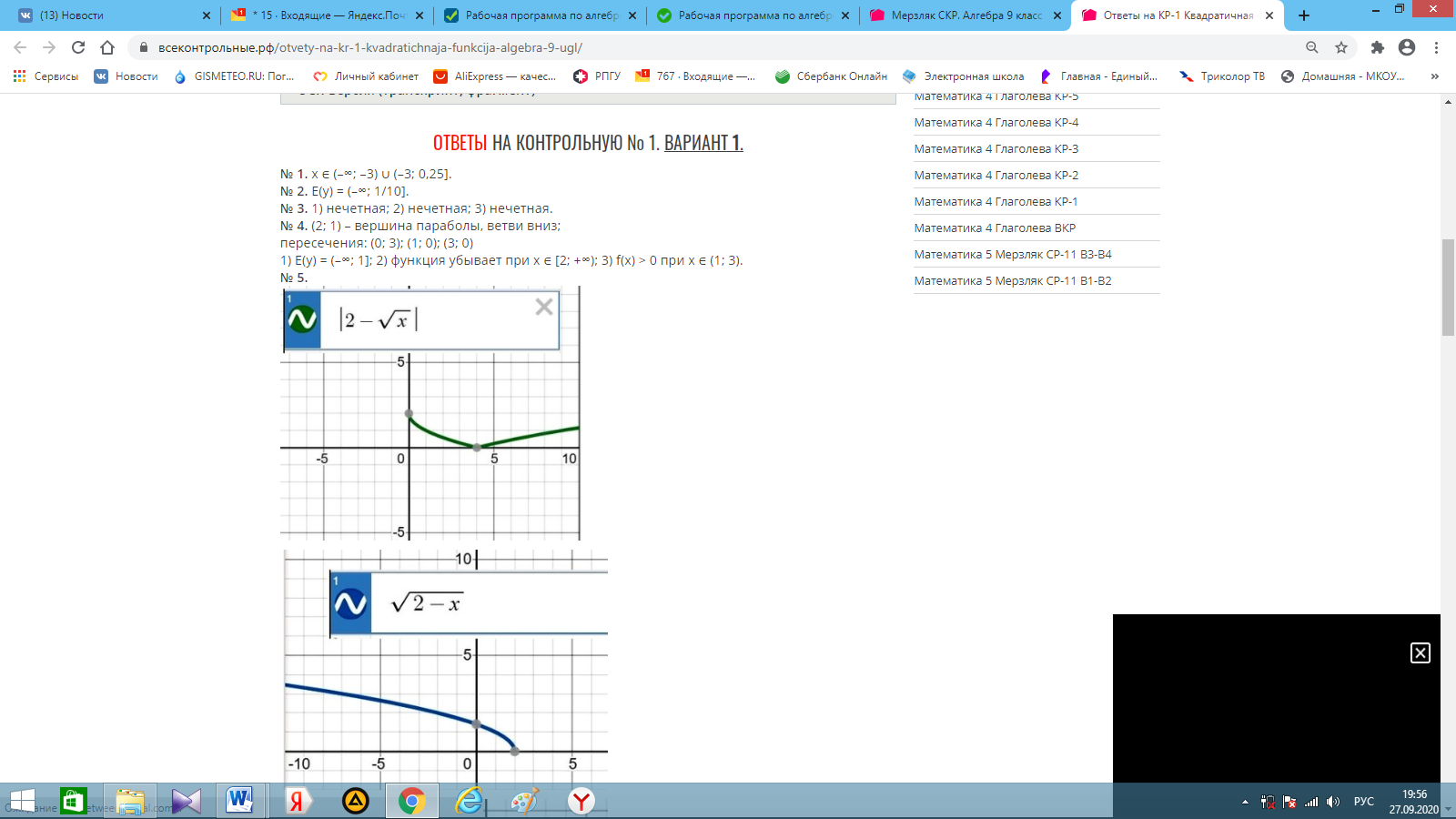
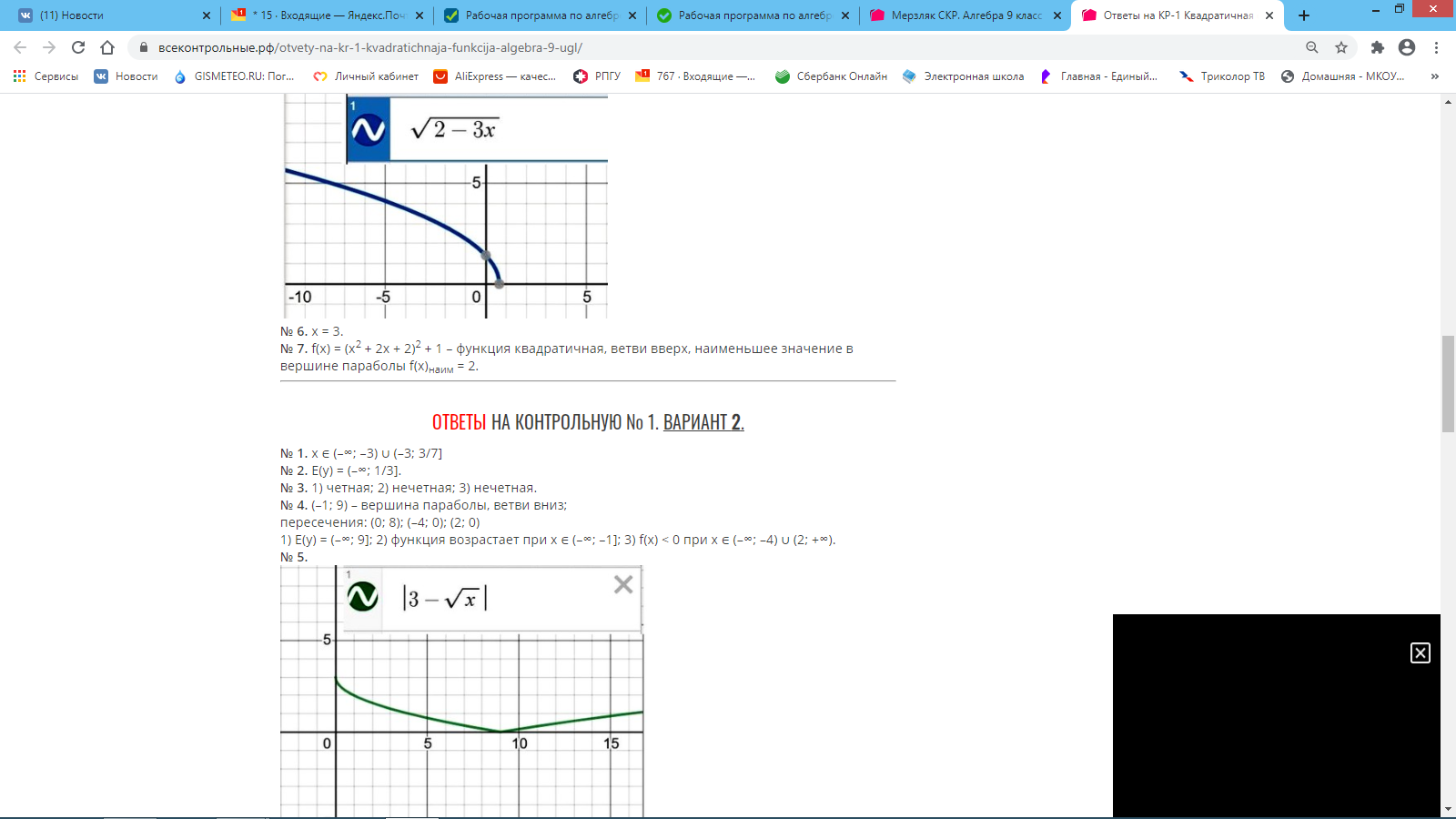
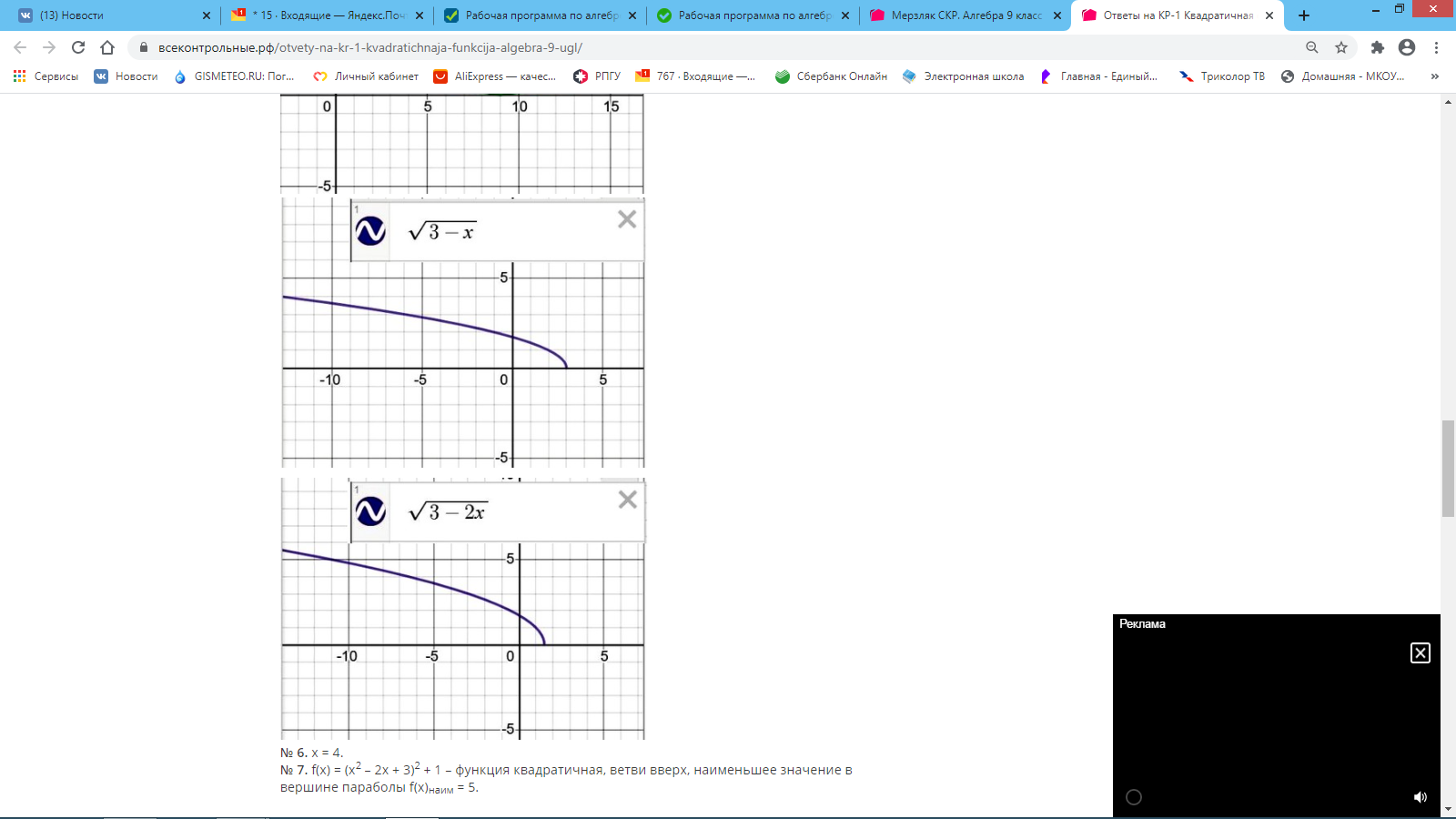
ОТВЕТЫ НА КОНТРОЛЬНУЮ № 2. ВАРИАНТ 1.

№ 1. 1) x ∈ (–∞; 1/9] ∪ [1; +∞);
2) x ∈ {1/4};
3) x ∈ (–∞; +∞).
№ 2. x ∈ [–2; 2) ∪ (2; 7];   Е(у) = (–∞; +∞).
№ 3. x ∈ [–3; 5].
№ 4. 1) x ∈ (–∞; –11) ∪ (–4; 3);
2) x ∈ {–4} ∪ (–1; 5);
3) x ∈ (–∞; –2] ∪ (–1; 2] ∪ (3; +∞).
№ 5. 1) x ∈ [–1; 1);    2) x ∈ [2; 3].
№ 6. a ∈ (–1; 0,5).

 

ОТВЕТЫ НА КОНТРОЛЬНУЮ № 2. ВАРИАНТ 2.

№ 1. 1) x ∈ [5/16; 1];
2) x ∈ (–∞; –1/5) ∪ (–1/5; +∞);
3) x ∈ (–∞; +∞).
№ 2. x ∈ [–3; 1) ∪ (1; 5];   Е(у) = (–∞; +∞).
№ 3. x ∈ [–3; –2) ∪ (1; 7].
№ 4. 1) x ∈ (–∞; –9) ∪ (–1; 2);
2) x ∈ [–6; 1];
3) x ∈ [–3; –2) ∪ [3; 5).
№ 5. 1) x ∈ (7; 12); 2) x ∈ (1; 6).
№ 6. a ∈ (–10; –1).

 

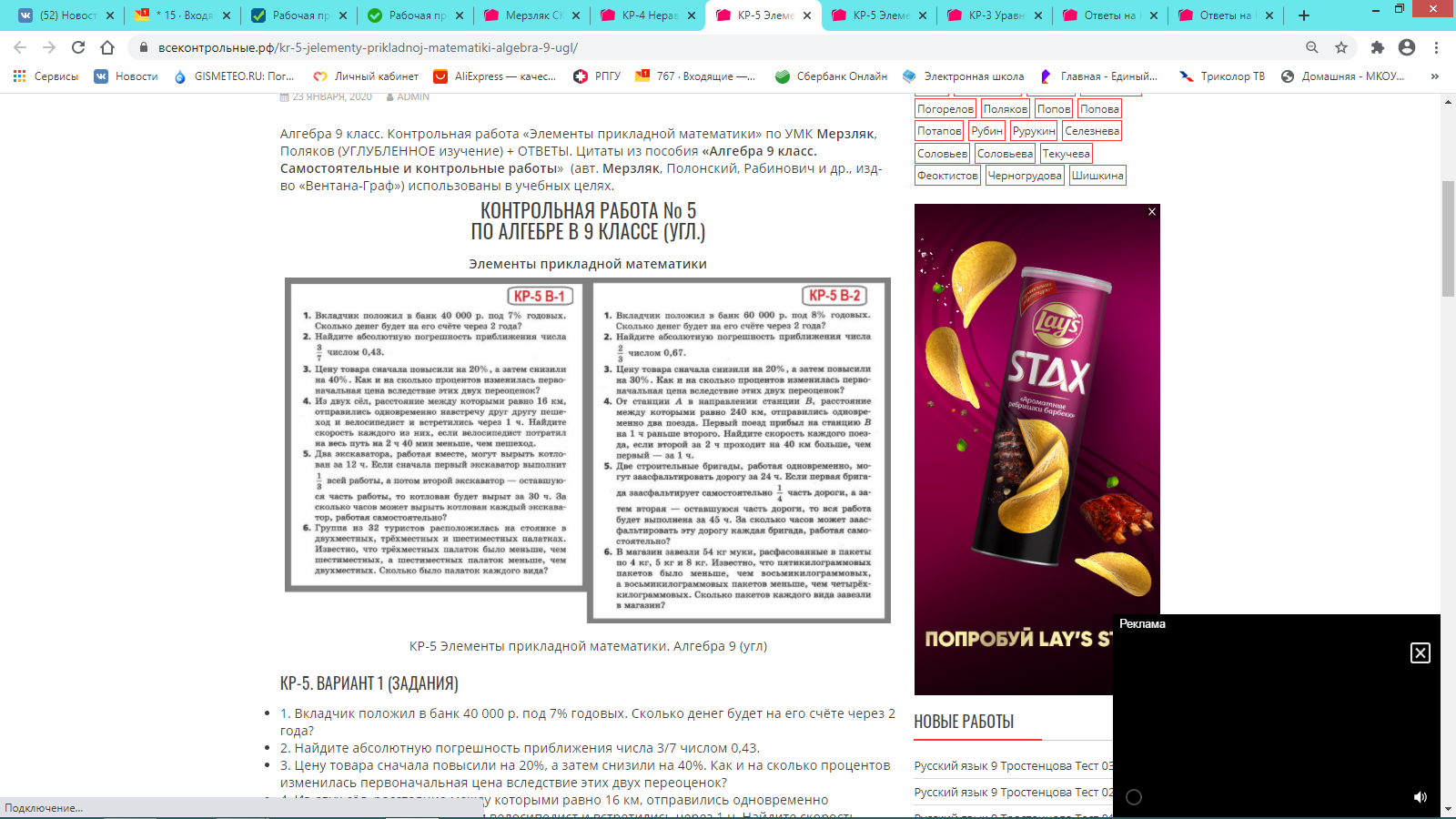
КР-5. ВАРИАНТ 1. ОТВЕТЫ

№ 1. 45 796 рублей.
№ 2. 1/700.
№ 3. Снизилась на 28%
№ 4. 4 км/ч и 12 км/ч.
№ 5. Два решения: Если первый может вырыть котлован за 60 часов, то второй за 15 часов. А если первый за 18 часов, то второй за 36 часов.
№ 6. Ответ: 4 двухместных, 3 шестиместных, 2 трехместных.

КР-5. ВАРИАНТ 2. ОТВЕТЫ

№ 1. 69 984 рубля
№ 2. 1/300.
№ 3. Повысилась на 4%.
№ 4. Скорость 1-го поезда 80км/ч, скорость 2-го поезда 60км/ч.
№ 5. Два решения: Если первая бригада может за 40 часов, то вторая за 60 часов. Если первая бригада может за 72 часа, то вторая – за 36 часов.
№ 6. Ответ: 2 пакета по 5 кг, 5 пакетов по 4 кг, 3 пакета по 8 кг.

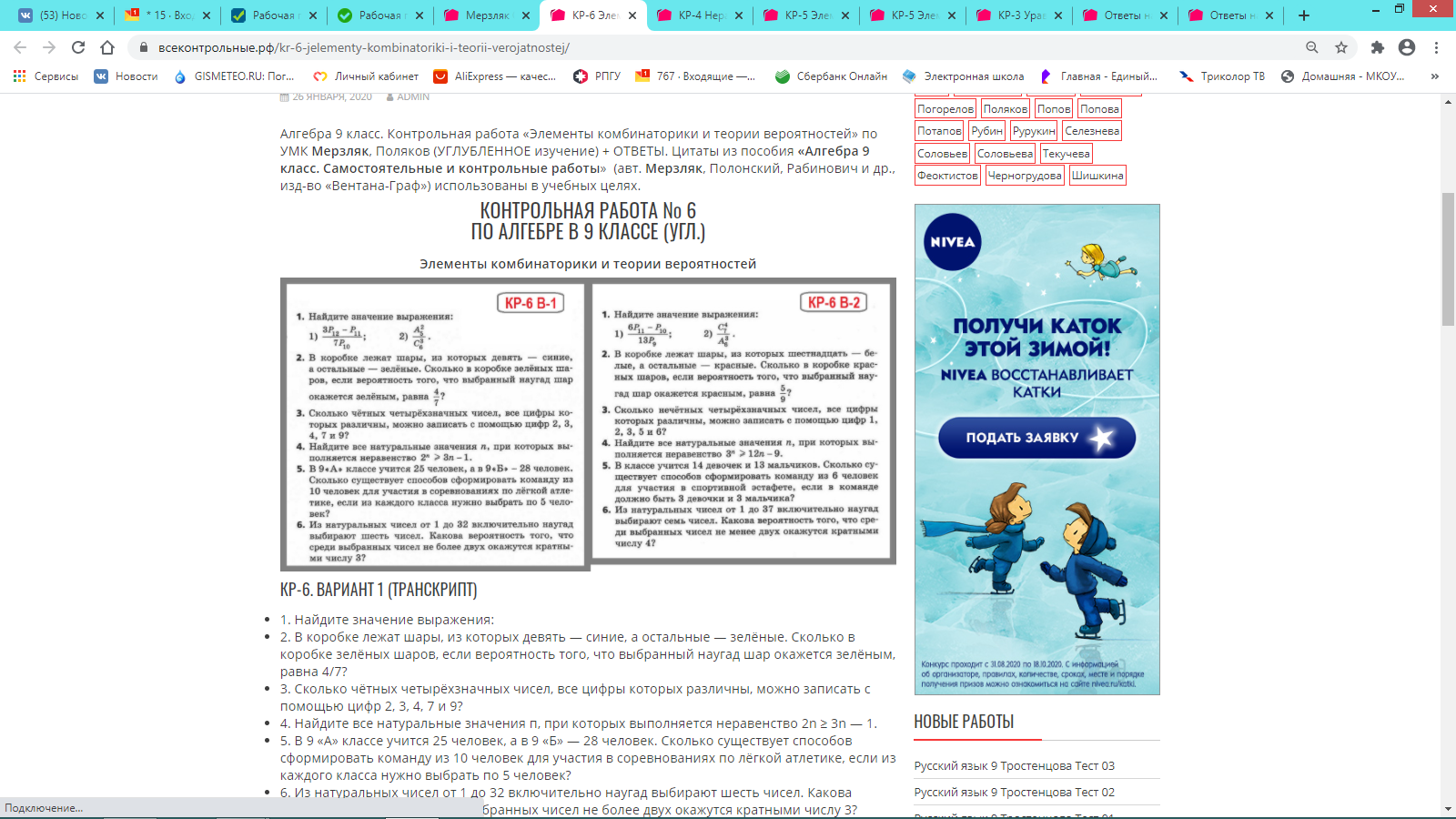
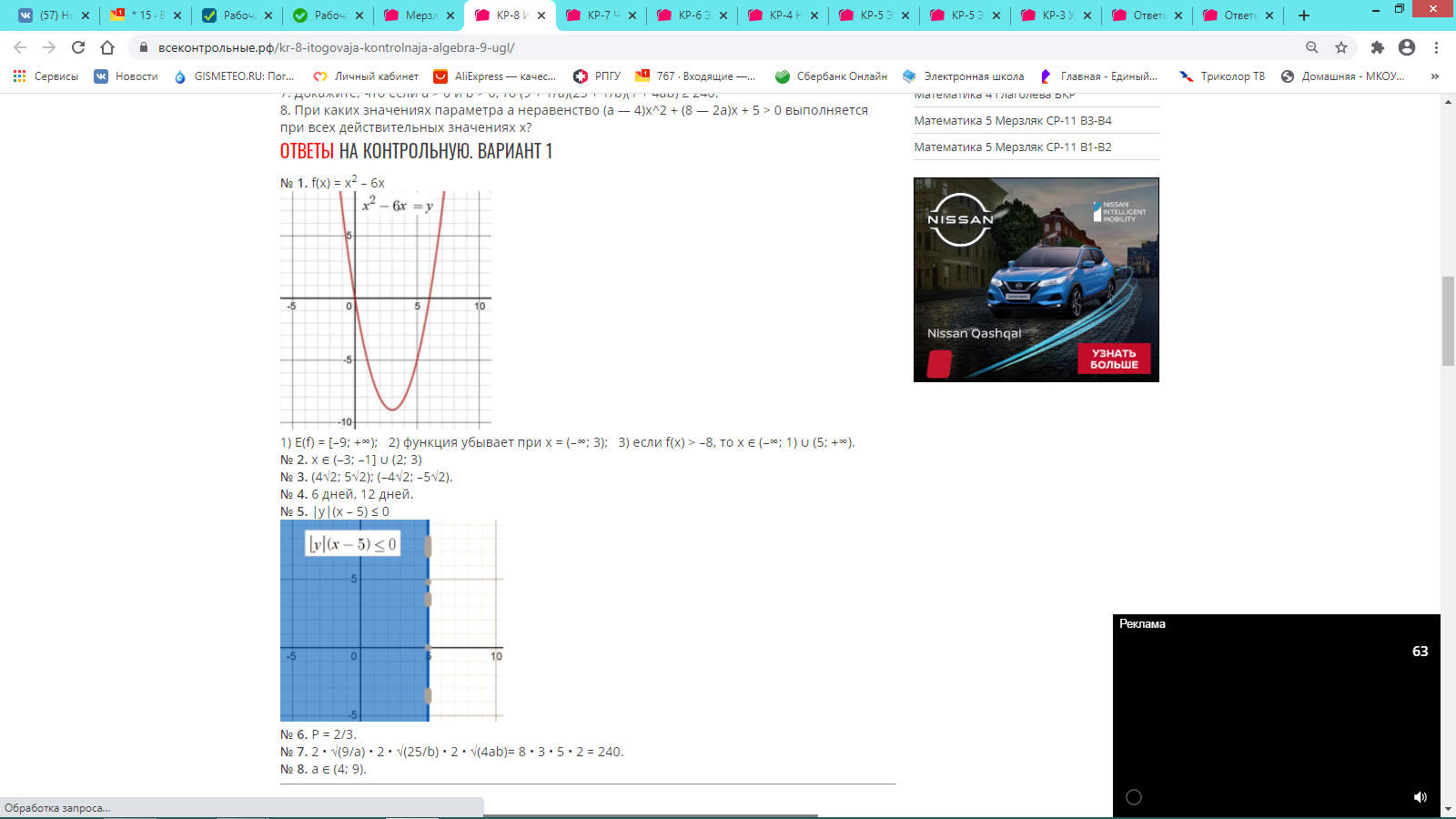
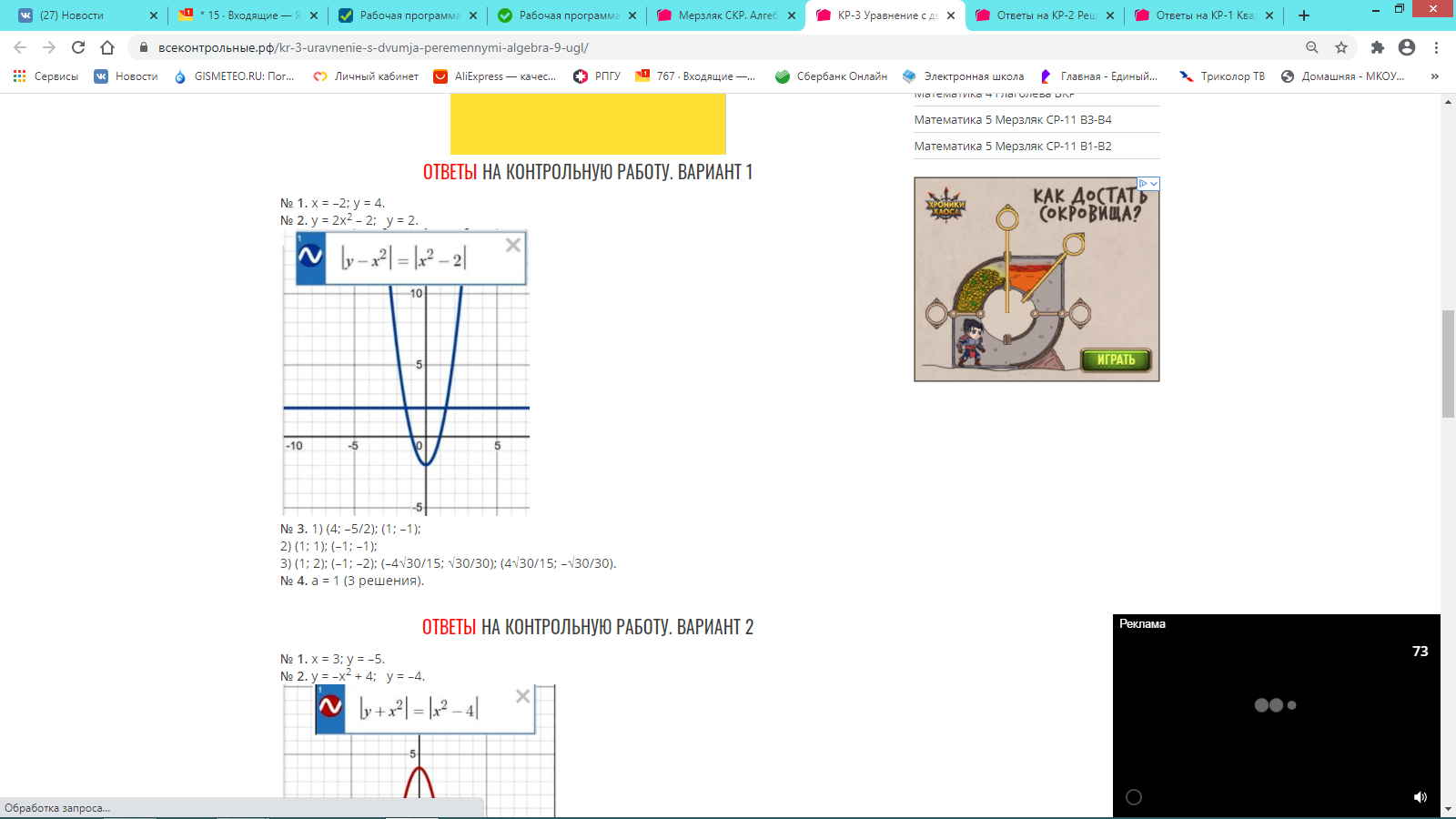
ОТВЕТЫ НА КОНТРОЛЬНУЮ. ВАРИАНТ 1

№ 1.   1) 55;   2) 1
№ 2.   12 зеленых шаров.
№ 3.   24 числа.
№ 4.   n = 1.
№ 5.   151 410 способов.
№ 6.   ⁴⁶/₇₁₉₂.

 

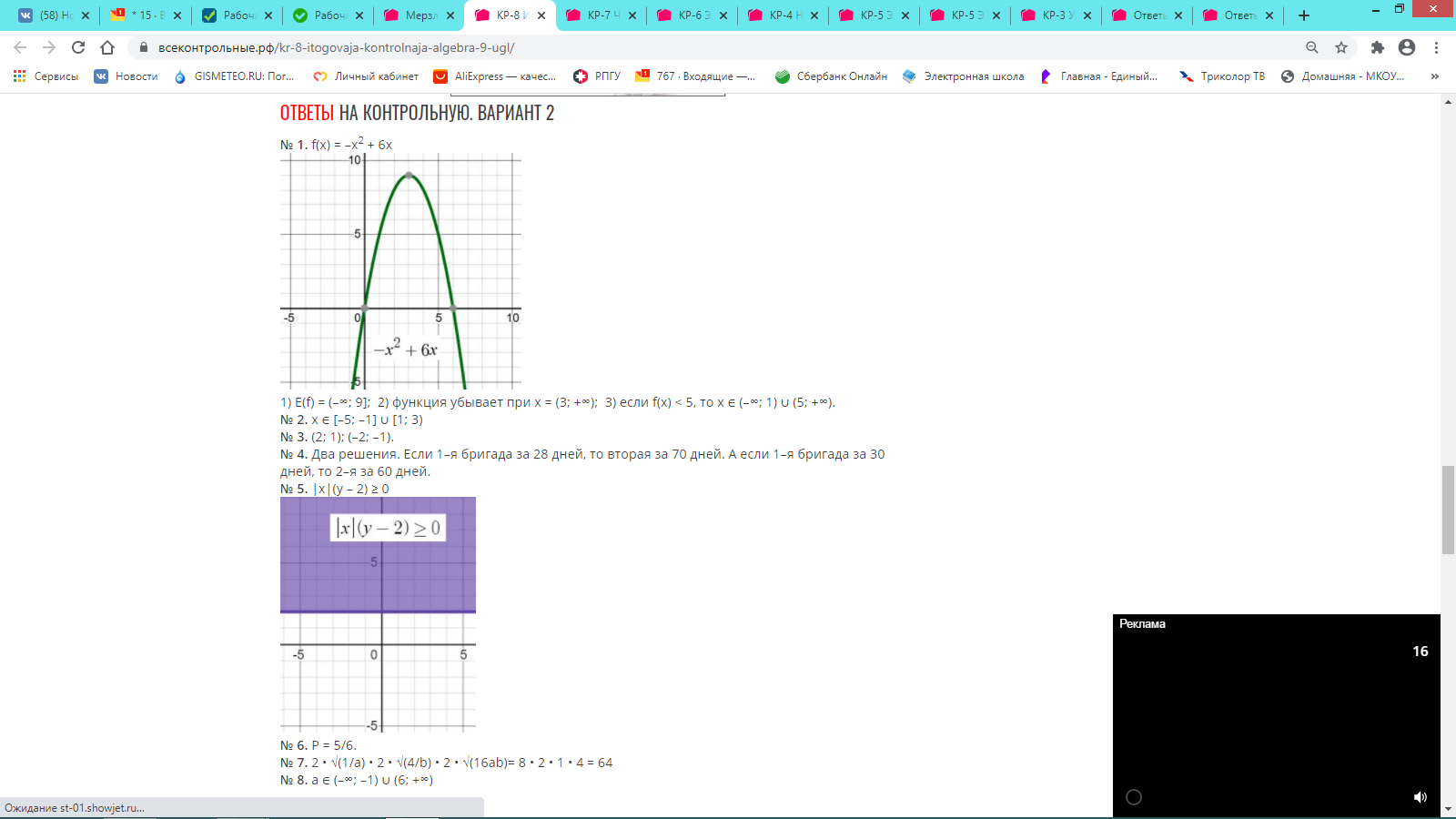
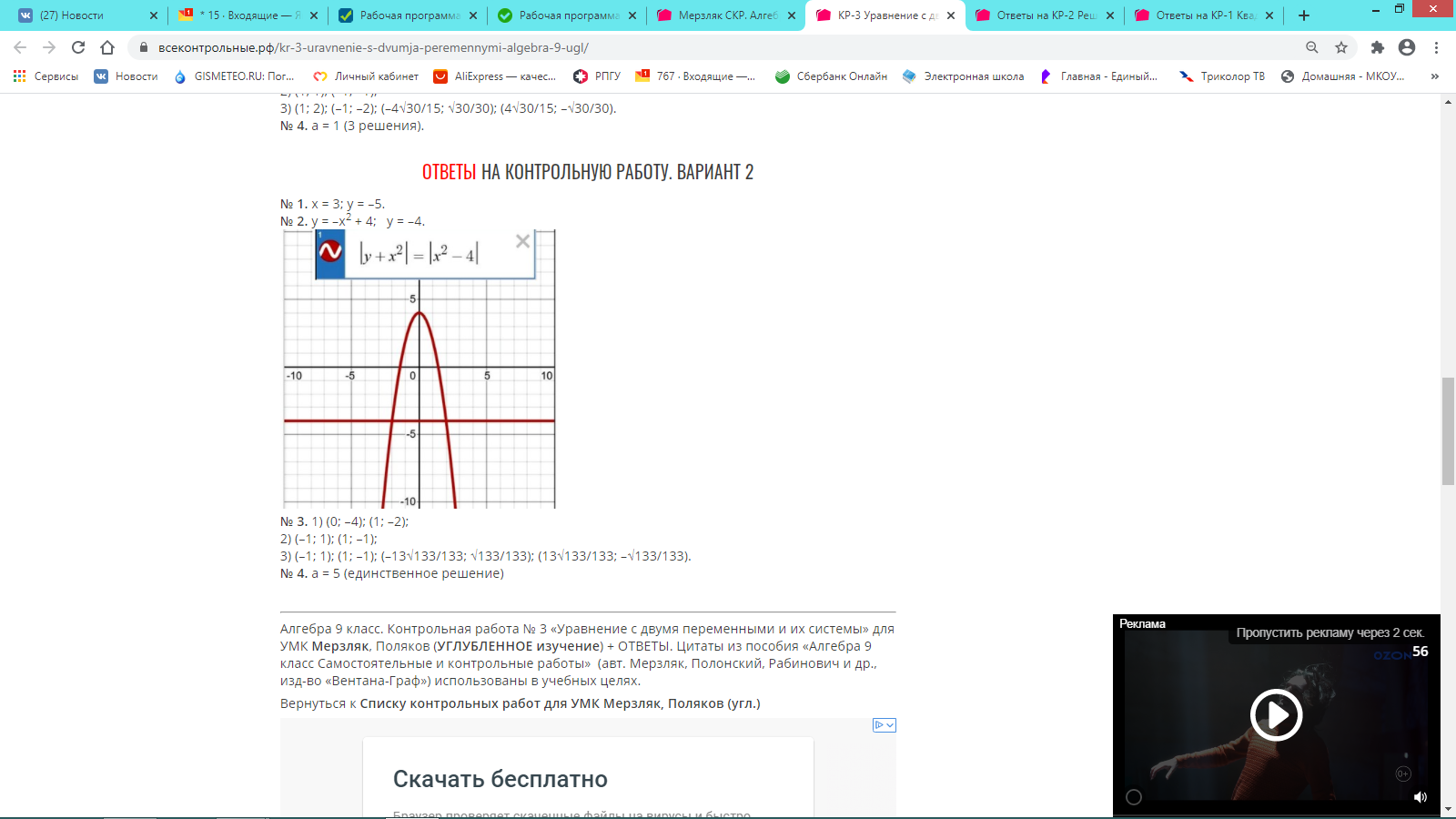
ОТВЕТЫ НА КОНТРОЛЬНУЮ. ВАРИАНТ 2

№ 1.    1) 50;    2) 7/24.
№ 2.    20 красных шаров.
№ 3.    72 числа.
№ 4.    n = 1.
№ 5.    650 способов.
№ 6.    ³/₈₅₇₉₅₆.

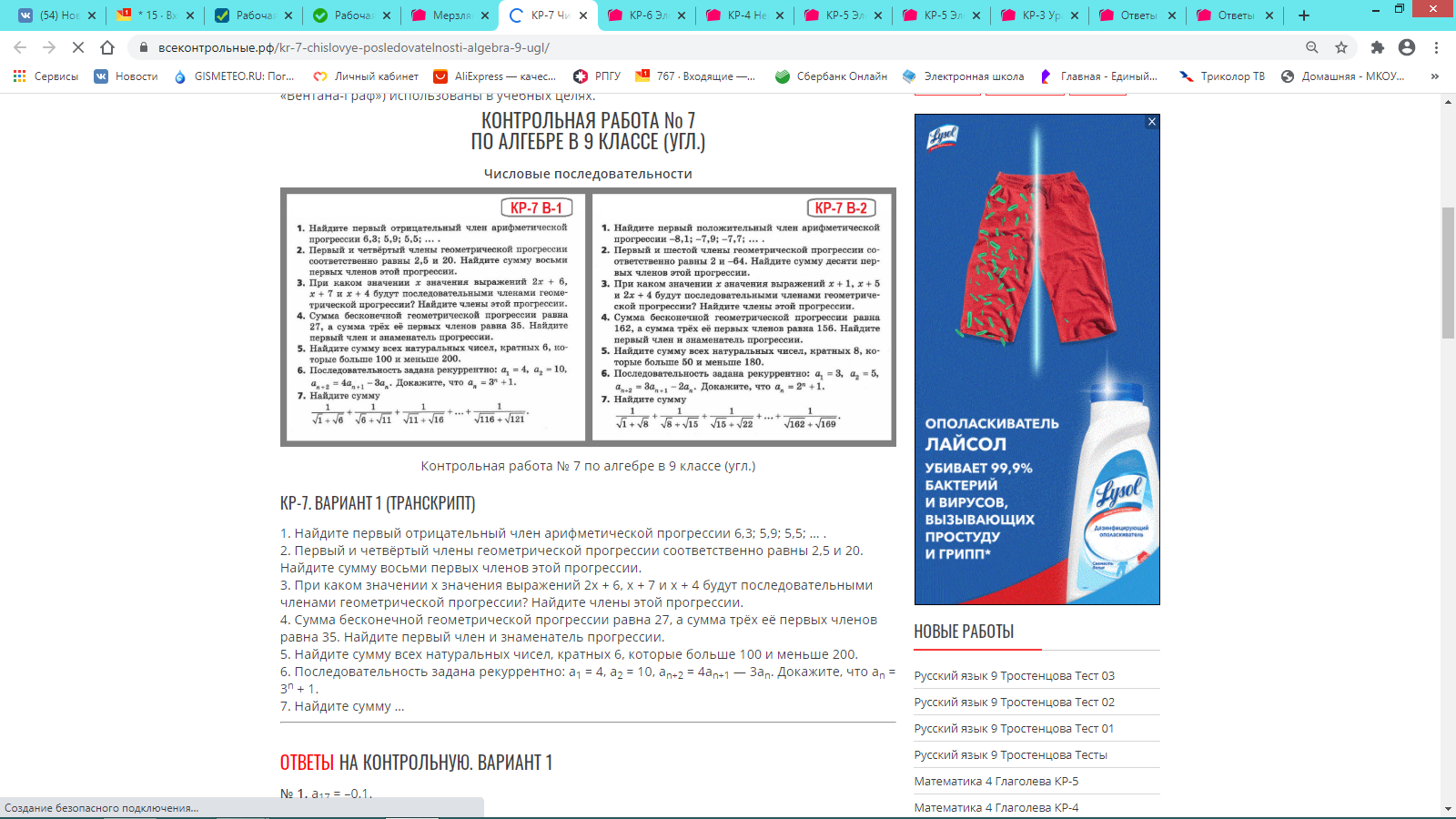
ОТВЕТЫ НА КОНТРОЛЬНУЮ. ВАРИАНТ 1

№ 1. а₁₇ = –0,1.
№ 2. S₈ = 637,5
№ 3. x = –5;   –4; 2; –1.
№ 4. b₁ = 9; q = 2/3.
№ 5. 2550.
№ 6. a₃ = 4a₂ – 3a₁ = 28.
a₁ = 4 = 3¹ + 1; a₂ = 10 = 3² + 1; a₃ = 28 = 3³ + 1 = a_n = 3ⁿ + 1.
№ 7. 1/(√(5n + 1) + √(5(n+1) + 1)), n ≤ 23, n ∈ N.

 

ОТВЕТЫ НА КОНТРОЛЬНУЮ. ВАРИАНТ 2

№ 1. a₂₃ = 0,7.
№ 2. S₁₀ = –682.
№ 3. x = 7;    8; 12; 18.
№ 4. b₁ = 216; q = 1/3.
№ 5. S₁₆ = 1856.
№ 6. a₃ = 3a₂ – 2a₁ = 9.
a₁ = 3 = 2¹ + 1; a₂ = 5 = 2² + 1; a₃ = 9 = 2³ + 1 = a_n = 2ⁿ + 1.
№ 7. 1/(√(7n + 1) + √(7(n+1) + 1)), n ≤ 23, n ∈ N