Муниципальное автономное общеобразовательное учреждение
с углубленным изучением математики и английского языка
«Школа дизайна «Точка» г. Перми
| Рассмотрена на заседании ШМО учителей математики. Протокол № 1 от 28.08.2020 | Утверждена приказом МАОУ «Школа дизайна «Точка» г. Перми От15.09. 2020 г. СЭД № 059-08/134-01-06/4136 |
РАБОЧАЯ ПРОГРАММА
по предмету
«Алгебра и начала математического анализа»
11 класс
на 2020 - 2021 учебный год
(база)
| Разработчик: Лепихина Екатерина Александровна, учитель математики
Составлена на основе Авторская программа Мордковича А.Г.. по математике для 11 класса (Программы. Математика. 5-6 классы. Алгебра. 7-9 классы. Алгебра и начала математического анализа. 10-11 классы/ авторы-составители И.И. Зубарева, А.Г. Мордкович, - 2-е издание, - М: Мнемозина, 2015).
|
Пермь, 2020г.
Пояснительная записка
Рабочая программа по математике составлена на основании следующих нормативно-правовых документов:
Федеральный закон № 273- ФЗ от 29.12.2012г. «Об образовании в Российской Федерации»
Федеральный государственный образовательный стандарт основного общего образования по математике, утвержденный приказом Минобразования России от 17 декабря 2010 г. № 1897
Авторская программа Мордковича А.Г.. по математике для 11 класса (Программы. Математика. 5-6 классы. Алгебра. 7-9 классы. Алгебра и начала математического анализа. 10-11 классы/ авторы-составители И.И. Зубарева, А.Г. Мордкович, - 2-е издание, - М: Мнемозина, 2015).
Положение о рабочей программе МАОУ с углублённым изучением математики и английского языка «Школа дизайна «Точка» г. Перми программа является основанием для определения качества реализации общего основного образования;
Учебный план МАОУ с углублённым изучением математики и английского языка «Школа дизайна «Точка» г. Перми программа является основанием для определения качества реализации общего основного образования на 2020 - 2021 учебный год.
Программа обеспечена учебником «Алгебра и начала математического анализа 11 класс» (профильный уровень), части 1 и 2, авторы А.Г. Мордкович, П.В. Семенов (Москва, Мнемозина, 2015). Программа предназначена для учащихся базового уровня, рассчитана на 136 часов, контрольных работ - 9. Преобладающей формой текущего контроля является письменный контроль.
Изучение математики в старшей школе на профильном уровне направлено на достижение следующих целей:
формирование представлений об идеях и методах математики; о математике как универсальном языке науки, средстве моделирования явлений и процессов;
овладение устным и письменным математическим языком, математическими знаниями и умениями, необходимыми для изучения школьных естественно-научных дисциплин, для продолжения образования и освоения избранной специальности на современном уровне;
развитие логического мышления, алгоритмической культуры, пространственного воображения, развитие математического мышления и интуиции, творческих способностей на уровне, необходимом для продолжения образования и для самостоятельной деятельности в области математики и ее приложений в будущей профессиональной деятельности;
воспитание средствами математики культуры личности: знакомство с историей развития математики, эволюцией математических идей, понимание значимости математики для общественного прогресса.
Особенности курса.
Особенностью предмета математика базового уровня в учебном плане школы является тот факт, что овладение основными понятиями и законами на базовом уровне стало необходимым практически каждому человеку в современной жизни. Математика возводится в ранг системообразующего предмета среди всех учебных предметов естественно- научного цикла и должна способствовать не только общему развитию, но и снабжать учащихся математическими методами познания, применение которых, способствует успешному участию в моделировании процессов, изучающихся в различных образовательных областях.
Общеучебные умения, навыки и способы деятельности.
Создать условия для умения логически обосновывать суждения, выдвигать гипотезы и понимать необходимость их проверки.
Создать условия для умения ясно, точно и грамотно выражать свои мысли в устной и письменной речи.
Формировать умение использовать различные языки математики: словесный, символический, графический.
Формировать умение свободно переходить с языка на язык для иллюстрации, интерпретации, аргументации и доказательства.
Создать условия для плодотворного участия в работе в группе; умения самостоятельно и мотивированно организовывать свою деятельность.
Формировать умение использовать приобретенные знания и умения в практической деятельности и повседневной жизни для исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств тел; вычисления площадей поверхностей пространственных тел при решении практических задач, используя при необходимости справочники и вычислительные устройства.
Создать условия для интегрирования в личный опыт новую, в том числе самостоятельно полученную информацию.
Формирование представлений об идеях и методах математики; о математике как универсальном языке науки, средстве моделирования явлений и процессов.
Овладение устным и письменным математическим языком, математическим знаниями и умениями, необходимыми для изучения школьных естественнонаучных дисциплин, для продолжения образования и освоения избранной специальности на современном уровне.
Развитие логического мышления, алгоритмической культуры, пространственного воображения, развитие математического мышления и интуиции, творческих способностей на уровне, необходимом для продолжения образования и для самостоятельной деятельности в области математики и ее приложений в будущей профессиональной деятельности.
Воспитание средствами математики культуры личности: знакомство с историей развития математики, эволюцией математических идей, понимания значимости математики для общественного прогресса.
Требования к уровню подготовки учащихся
В результате освоения курса математики 11 класса учащиеся должны овладеть следующими знаниями, умениями и навыками.
Личностным результатом изучения предмета является формирование следующих умений и качеств:
сформированность ответственного отношения к учению, готовность и способности обучающихся к саморазвитию, выбору дальнейшего образования на базе ориентировки в мире профессий и профессиональных предпочтений, осознанному построению индивидуальной образовательной траектории с учётом устойчивых познавательных интересов;
сформированность целостного мировоззрения, соответствующего современному уровню развития науки и общественной практики;
представление о математической науке как о сфере человеческой деятельности, об этапах её развития, о её значимости для развития цивилизации;
критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
креативность мышления, инициатива, находчивость, активность при решении задач.
Метапредметным результатом изучения курса является формирование универсальных учебных действий (УУД).
Регулятивные УУД:
•умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера, вместе с учителем или самостоятельно обнаруживать и формулировать учебную проблему, определять цель УД;
• с помощью учителя или самостоятельно выдвигать версии решения проблемы, осознавать (и интерпретировать в случае необходимости) конечный результат, выбирать средства достижения цели из предложенных, а также искать их самостоятельно;
• составлять (индивидуально, или в группе, или с помощью учителя) алгоритм решения проблемы (выполнения проекта);
• работая по алгоритму, сверять свои действия с целью и при необходимости исправлять ошибки самостоятельно (в том числе и корректировать алгоритм);
• в диалоге с учителем совершенствовать самостоятельно выбранные критерии оценки.
Познавательные УУД:
проводить наблюдение и эксперимент, выдвигать гипотезы;
осуществлять расширенный поиск информации с использованием ресурсов библиотек и Интернета;
осуществлять выбор наиболее эффективных и оптимальных способов решения задач в зависимости от конкретных условий;
владеть логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев;
устанавливать причинно-следственные связи, строить логическое рассуждение, умозаключение и выводы;
давать определения понятиям.
Коммуникативные УУД:
самостоятельно организовывать учебное сотрудничество и совместную деятельность с учителями и сверстниками, распределять функции и роли участников, взаимодействие и общие способы работы;
умение работать в группе, паре, находить общее решение и разрешать конфликты на основе согласования позиций и учета интересов;
овладение символьным языком алгебры;
в дискуссии уметь выдвинуть аргументы и контраргументы;
слушать партнёра, формулировать аргументировать и отстаивать своё мнение.
Предметным результатом изучения курса является сформированность следующих знаний/умений.
решают задачи, возникающие в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
знают значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии;
универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
вероятностный характер различных процессов окружающего мира;
определяют значение функции по значению аргумента при различных способах задания функции;
строят графики изученных функций;
описывают по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;
решают уравнения, простейшие системы уравнений, используя свойства функций и их графиков; используют приобретенные знания и умения в практической деятельности и повседневной жизни для:
описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков;
используют приобретенные знания и умения в практической деятельности и повседневной жизни для: построения и исследования простейших математических моделей.
Принимая во внимание специфику школы, для такого предмета как математика обязательными формами текущего контроля устанавливаются
контрольные точки. Контрольная точка - контрольное мероприятие рубежного контроля, зафиксированное по времени и по форме проведения. Школьным методическим объединением устанавливаются сроки проведения контрольных точек, их тематика и формат проведения. Количество контрольных точек по предмету не должно быть менее двух в четверть. Годовая оценка по предмету не может быть выставлена при условии 2/3 от общего количества не сданных контрольных точек. Учитель обязан своевременно осуществить проверку и в течение не более трех дней довести ее результат до сведения обучающихся и их родителей. Информация о сроках проведения и темах контрольных точек выкладывается на сайте образовательной организации. Критерии и нормы оценки знаний, умений и навыков обучающихся по алгебре и началам анализа
Оценка письменных контрольных работ.
Каждая контрольная работа состоит из нескольких заданий различного уровня сложности, заданиям ставятся в соответствие баллы. Наибольшее количество баллов в каждой работе 10. Оценивание качества выполнения учащимся контрольной работы осуществляется по количеству набранных им баллов. Если задание высокого уровня сложности выполнено не в полном объеме, но решение содержит существенные продвижение в поиске ответа или допущена вычислительная ошибка, приведшая ученика к неправильному ответу, то может присваиваться часть объявленного балла. Баллы суммируются, оценка в журнал выставляется в соответствии с таблицей.
| Общеобразовательный класс | Класс с углублённым изучением предмета | Для детей ОВЗ |
| Балл | оценка | балл | оценка | балл | оценка |
| 9-10 | 5 | 9-10 | 5 | 8,5-10 | 5 |
| 7-8,5 | 4 | 7,5-8.5 | 4 | 6,5-8 | 4 |
| 5-6,5 | 3 | 6-7 | 3 | 3,5-6 | 3 |
| Ниже 5 баллов | 2 | Ниже 6 баллов | 2 | Ниже 3,5 баллов | 2 |
Учитель может повысить балл за оригинальный ответ на вопрос или нестандартное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
2. Оценка устных ответов.
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна – две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала;
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Содержание
Тема 1 . Степени и корни. Степенные функции.(15 часов)
Корни и степени. Корень степени n1 и его свойства. Степень с рациональным показателем и ее свойства. Понятие о степени с действительным показателем. Свойства степени с действительным показателем. Степенные функции, их свойства и графики.
Тема 2. Показательная и логарифмическая функции (24 часа)
Логарифм. Логарифм числа. Основное логарифмическое тождество. Логарифм произведения, частного, степени; переход к новому основанию. Десятичный и натуральный логарифмы, число е. Преобразования простейших выражений, включающих арифметические операции, а также операцию возведения в степень и операцию логарифмирования.
Показательная и логарифмическая функции, их свойства и графики. Показательные и логарифмические уравнения и неравенства. Дифференцирование показательной и логарифмической функций.
Тема 3. Первообразная и интеграл.(9 часов)
Тема№4. Элементы комбинаторики, статистики и теории вероятности. (6 часов)
Табличное и графическое представление данных. Числовые характеристики рядов данных. Поочередный и одновременный выбор нескольких элементов из конечного множества. Формулы числа перестановок, сочетаний, размещений. Решение комбинаторных задач. Формула бинома Ньютона. Свойства биномиальных коэффициентов. Треугольник Паскаля. Элементарные и сложные события. Рассмотрение случаев и вероятность суммы несовместных событий, вероятность противоположного события. Понятие о независимости событий. Вероятность и статистическая частота наступления события. Решение практических задач с применением вероятностных методов.
Тема№5. УРАВНЕНИЯ И НЕРАВЕНСТВА. Системы уравнений и неравенств.(17 часов)
Равносильность уравнений, неравенств, систем. Общие методы решения уравнений. Решение неравенств с одной переменной. Уравнения и неравенства с двумя переменными. Система уравнений. Уравнения и неравенства с параметрами.
Повторение 25 часов. Резерв 2 часа.
Календарно-тематический план
| Тема, количество часов | № урока | Тема урока | Деятельность учащихся | Формы контроля |
| Повторение 6 часов | 1-6
| Числовые выражения Преобразования корней. Алгебраические уравнения Тригонометрия Производная | Решают простейшие тригонометрические уравнения, применяют основные приемы решения тригонометрических уравнений, вводят новую переменную в решении уравнений и основные алгоритмические приемы | Тестирование |
| Степени и корни. Степенные функции. 15 часов | 7-8 | Понятие корня 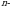 степени из действительного числа. степени из действительного числа. | Обобщают и систематизируют знания о степенной функции, исследуют степенную функцию, используя алгоритм, решают простейшие иррациональные уравнения | Тестирование
Самостоятельная работа Тестирование Самостоятельная работа
Тестирование |
| 9-10 | Функция вида 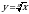 , их свойства и графики , их свойства и графики |
| 11-12 | Свойства корня 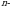 степени степени |
| 13-15 | Преобразование выражений, содержащих радикалы |
| 16 | Контрольная работа |
| 17-18 | Обобщение понятия о показателе степени |
| 19-21 | Степенные функции, их свойства и графики |
| Показательная и логарифмическая функции 24 часа | 22-24 | Показательная функция, ее свойства и график | Определяют показательную и логарифмическую функции, проводят исследование функции, используя алгоритм, строят графики показательной и логарифмической функций, решают показательные и логарифмические уравнения и неравенства, используя алгоритм. | Самостоятельная работа Самостоятельная работа
Тестирование Самостоятельная работа
Тестирование Самостоятельная работа Тестирование |
| 25-27 | Показательные уравнения и неравенства |
| 28 | Контрольная работа |
| 29 | Понятие логарифма |
| 30-31 | Функция 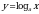 , ее свойства и график , ее свойства и график |
| 32-33 | Свойства логарифмов |
| 34-36 | Логарифмические уравнения |
| 37 | Контрольная работа |
| 38-40 | Логарифмические неравенства |
| 41-42 | Переход к новому основанию логарифма |
| 43-44 | Дифференцирование показательной и логарифмической функции |
| 45 | Контрольная работа |
| Первообразная и интеграл 9 часов | 46-48 | Первообразная | Определяют первообразную, используют таблицу первообразных в решении задач, находят первообразные заданных функций, находят площади фигур, используя формулу Ньютона-Лейбница | Самостоятельная работа Тестирование
|
| 49-51 | Определенный интеграл |
| 52 | Контрольная работа |
| 53-54 | Резерв |
| Элементы математической статистики, комбинаторики и теории вероятностей 6 часов | 55 | Статистическая обработка данных | Решают простейшие комбинаторные задачи, рассматривая дерево возможных вариантов, правило умножения; указывают общий ряд данных измерений, наименьшую и наибольшую варианты, определяют кратность варианты, процентную частоту, строят многоугольник процентных частот; находят вероятность события, применяя классическую вероятностную схему, классическое определение вероятности, случайное событие, достоверное и невозможное события, несовместные события, события, противоположные данному событию; решают простейшие статистические задачи; решают простейшие комбинаторные и вероятностные задачи.
|
Самостоятельная работа |
| 56 | Простейшие вероятностные задачи |
| 57 | Сочетания и размещения |
| 58 | Формула бинома Ньютона |
| 59 | Случайные события и их вероятности |
| 60 | Контрольная работа |
| Уравнения и неравенства 17 часов | 61-62 | Равносильность уравнений | Выполняют равносильные преобразования уравнений и неравенств с двумя переменными, определяют понятия, приводят доказательства; решают уравнения, содержащие параметр, используют метод подстановки, метод алгебраического сложения, методом введения новых переменных; составляют математические модели реальных ситуаций, и работаю с составленной моделью; составляют математические модели реальных ситуаций и работают с составленной моделью. | Самостоятельная работа
Самостоятельная работа Тестирование
|
| 63-65 | Общие методы решения уравнений |
| 66-68 | Решения неравенств с одной переменной |
| 69 | Уравнения и неравенства с двумя переменными |
| 70-72 | Системы уравнений |
| 73-75 | Уравнения и неравенства с параметрами |
| 76-77 | Контрольная работа |
| Повторение 25 часов | 78-100 101-102 | Повторение материал Итоговый тест в формате ЕГЭ | Решают тестовые задания в формате ЕГЭ |
Тестирование |






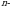 степени из действительного числа.
степени из действительного числа.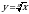 , их свойства и графики
, их свойства и графики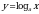 , ее свойства и график
, ее свойства и график









