СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ

Благодаря готовым учебным материалам для работы в классе и дистанционно

Выбрать материалы

Скидки до 50 % на комплекты
только до

Готовые ключевые этапы урока всегда будут у вас под рукой

Организационный момент

Проверка знаний

Объяснение материала

Закрепление изученного

Итоги урока

Обо мне Блог Файлы Тесты Галерея Активность Награды

Рабочая программа по математике

Категория: Математика

Нажмите, чтобы узнать подробности

Рабочая программа по математике для обучающихся 10-11 классов

Просмотр содержимого документа
«Рабочая программа по математике»

  1. Планируемые результаты освоения учебного предмета

Программа предполагает достижение выпускниками старшей школы следующих личностных, метапредметных и предметных результатов.

Личностные результаты освоения основной образовательной программы школы отражают:

— целостность мировоззрения, соответствующего современному уровню развития науки математики и общественной практики ее применения;

— основ саморазвития и самовоспитания в соответствии с общечеловеческими ценностями и идеалами гражданского общества; готовности и способности к самостоятельной, творческой и ответственной деятельности с применением методов математики;

— готовности и способности к образованию, в том числе самообразованию, на протяжении всей жизни; сознательного отношения к непрерывному образованию как условию успешной профессиональной и общественной деятельности на основе развитой мотивации учебной деятельности и личностного смысла изучения математики, заинтересованности в приобретении и расширении математических знаний и способов действий, осознанности в построении индивидуальной образовательной траектории;



— осознанного выбора будущей профессии, ориентированной в применении математических методов и возможностей реализации собственных жизненных планов; отношения к профессиональной деятельности как возможности участия в решении личных, общественных, государственных, общенациональных проблем;



— логического мышления: критичности (умение распознавать логически некорректные высказывания), креативности (собственная аргументация, опровержения, постановка задач, формулировка проблем, работа над исследовательским проектом и др.).

Планируемые метапредметные результаты освоения ОП

Метапредметные результаты освоения ОП представлены тремя группами универсальных учебных действий (УУД).





Регулятивные универсальные учебные действия

Выпускник научится:

  • самостоятельно определять цели, задавать параметры и критерии, по которым можно определить, что цель достигнута;

  • оценивать возможные последствия достижения поставленной цели в деятельности, собственной жизни и жизни окружающих людей, основываясь на соображениях этики и морали;

  • ставить и формулировать собственные задачи в образовательной деятельности и жизненных ситуациях;

  • оценивать ресурсы, в том числе время и другие нематериальные ресурсы, необходимые для достижения поставленной цели;

  • выбирать путь достижения цели, планировать решение поставленных задач, оптимизируя материальные и нематериальные затраты;

  • организовывать эффективный поиск ресурсов, необходимых для достижения поставленной цели;

  • сопоставлять полученный результат деятельности с поставленной заранее целью.

Познавательные универсальные учебные действия

Выпускник научится:

  • искать и находить обобщенные способы решения задач, в том числе, осуществлять развернутый информационный поиск и ставить на его основе новые (учебные и познавательные) задачи;

  • критически оценивать и интерпретировать информацию с разных позиций, распознавать и фиксировать противоречия в информационных источниках;

  • использовать различные модельно-схематические средства для представления существенных связей и отношений, а также противоречий, выявленных в информационных источниках;

  • находить и приводить критические аргументы в отношении действий и суждений другого; спокойно и разумно относиться к критическим замечаниям в отношении собственного суждения, рассматривать их как ресурс собственного развития;

  • выходить за рамки учебного предмета и осуществлять целенаправленный поиск возможностей для широкого переноса средств и способов действия;

  • выстраивать индивидуальную образовательную траекторию, учитывая ограничения со стороны других участников и ресурсные ограничения;

  • менять и удерживать разные позиции в познавательной деятельности.

Коммуникативные универсальные учебные действия

Выпускник научится:

  • осуществлять деловую коммуникацию как со сверстниками, так и со взрослыми (как внутри образовательной организации, так и за ее пределами), подбирать партнеров для деловой коммуникации исходя из соображений результативности взаимодействия, а не личных симпатий;

  • при осуществлении групповой работы быть как руководителем, так и членом команды в разных ролях (генератор идей, критик, исполнитель, выступающий, эксперт и т.д.);

  • координировать и выполнять работу в условиях реального, виртуального и комбинированного взаимодействия;

  • развернуто, логично и точно излагать свою точку зрения с использованием адекватных (устных и письменных) языковых средств;

  • распознавать конфликтогенные ситуации и предотвращать конфликты до их активной фазы, выстраивать деловую и образовательную коммуникацию, избегая личностных оценочных суждений.





Предметные результаты.

В результате изучения учебного предмета «Математика» на уровне среднего общего образования:

Выпускник на базовом уровне научится:

- оперировать на базовом уровне понятиями: целое число, делимость чисел, обыкновенная дробь, десятичная дробь, рациональное число, приближённое значение числа, часть, доля, отношение, процент, повышение и понижение на заданное число процентов, масштаб;

- оперировать на базовом уровне понятиями: логарифм числа, тригонометрическая окружность, градусная мера угла, величина угла, заданного точкой на тригонометрической окружности, синус, косинус, тангенс и котангенс углов, имеющих произвольную величину;

- выполнять арифметические действия с целыми и рациональными числами;

- выполнять несложные преобразования числовых выражений, содержащих степени чисел, либо корни из чисел, либо логарифмы чисел;

- сравнивать рациональные числа между собой;

- оценивать и сравнивать с рациональными числами значения целых степеней чисел, корней натуральной степени из чисел, логарифмов чисел в простых случаях;

- изображать точками на числовой прямой целые и рациональные числа;

- изображать точками на числовой прямой целые степени чисел, корни натуральной степени из чисел, логарифмы чисел в простых случаях;

- выполнять несложные преобразования целых и дробно-рациональных буквенных выражений;

- выражать в простейших случаях из равенства одну переменную через другие;

- вычислять в простых случаях значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;

- изображать схематически угол, величина которого выражена в градусах;

- оценивать знаки синуса, косинуса, тангенса, котангенса конкретных углов.

- решать линейные уравнения и неравенства, квадратные уравнения;

- решать логарифмические уравнения вида log a (bx + c) = d и простейшие неравенства вида log a x

- приводить несколько примеров корней простейшего тригонометрического уравнения вида: sin x = a, cos x = a, tg x = a, ctg x = a, где a – табличное значение соответствующей тригонометрической функции.

- решать показательные уравнения и простейшие неравенства;

- оперировать на базовом уровне понятиями: зависимость величин, функция, аргумент и значение функции, область определения и множество значений функции, график зависимости, график функции, нули функции, промежутки знакопостоянства, возрастание на числовом промежутке, убывание на числовом промежутке, наибольшее и наименьшее значение функции на числовом промежутке, периодическая функция, период;

- оперировать на базовом уровне понятиями: прямая и обратная пропорциональность линейная, квадратичная, логарифмическая и показательная функции, тригонометрические функции;

- распознавать графики элементарных функций: прямой и обратной пропорциональности, линейной, квадратичной, логарифмической и показательной функций, тригонометрических функций;

- соотносить графики элементарных функций: прямой и обратной пропорциональности, линейной, квадратичной, логарифмической и показательной функций, тригонометрических функций с формулами, которыми они заданы;

- находить по графику приближённо значения функции в заданных точках;

- определять по графику свойства функции (нули, промежутки знакопостоянства, промежутки монотонности, наибольшие и наименьшие значения и т.п.);

- строить эскиз графика функции, удовлетворяющей приведенному набору условий (промежутки возрастания / убывания, значение функции в заданной точке, точки экстремумов и т.д.).

- оперировать на базовом уровне понятиями: производная функции в точке, касательная к графику функции, производная функции;

- определять значение производной функции в точке по изображению касательной к графику, проведенной в этой точке;

- решать несложные задачи на применение связи между промежутками монотонности и точками экстремума функции, с одной стороны, и промежутками знакопостоянства и нулями производной этой функции – с другой.

- оперировать на базовом уровне основными описательными характеристиками числового набора: среднее арифметическое, медиана, наибольшее и наименьшее значения;

- оперировать на базовом уровне понятиями: частота и вероятность события, случайный выбор, опыты с равновозможными элементарными событиями;

- вычислять вероятности событий на основе подсчета числа исходов.

- решать несложные текстовые задачи разных типов;

- анализировать условие задачи, при необходимости строить для ее решения математическую модель;

- понимать и использовать для решения задачи информацию, представленную в виде текстовой и символьной записи, схем, таблиц, диаграмм, графиков, рисунков;

- действовать по алгоритму, содержащемуся в условии задачи;

- использовать логические рассуждения при решении задачи;

- работать с избыточными условиями, выбирая из всей информации, данные, необходимые для решения задачи;

- осуществлять несложный перебор возможных решений, выбирая из них оптимальное по критериям, сформулированным в условии;

- анализировать и интерпретировать полученные решения в контексте условия задачи, выбирать решения, не противоречащие контексту;

- решать задачи на расчет стоимости покупок, услуг, поездок и т.п.;

- решать задачи на простые проценты (системы скидок, комиссии) и на вычисление сложных процентов в различных схемах вкладов, кредитов и ипотек;

- оперировать на базовом уровне понятиями: точка, прямая, плоскость в пространстве, параллельность и перпендикулярность прямых и плоскостей;

- распознавать основные виды многогранников (призма, пирамида, прямоугольный параллелепипед, куб);

- изображать изучаемые фигуры от руки и с применением простых чертежных инструментов;

- делать (выносные) плоские чертежи из рисунков простых объемных фигур: вид сверху, сбоку, снизу;

- извлекать информацию о пространственных геометрических фигурах, представленную на чертежах и рисунках;

- применять теорему Пифагора при вычислении элементов стереометрических фигур;

- находить объемы и площади поверхностей простейших многогранников с применением формул;

- распознавать основные виды тел вращения (конус, цилиндр, сфера и шар);

- находить объемы и площади поверхностей простейших многогранников и тел вращения с применением формул.

- оперировать на базовом уровне понятием декартовы координаты в пространстве;

- находить координаты вершин куба и прямоугольного параллелепипеда.

Выпускник на базовом уровне получит возможность научиться:

- свободно оперировать понятиями: целое число, делимость чисел, обыкновенная дробь, десятичная дробь, рациональное число, приближённое значение числа, часть, доля, отношение, процент, повышение и понижение на заданное число процентов, масштаб;

- приводить примеры чисел с заданными свойствами делимости;

- оперировать понятиями: логарифм числа, тригонометрическая окружность, радианная и градусная мера угла, величина угла, заданного точкой на тригонометрической окружности, синус, косинус, тангенс и котангенс углов, имеющих произвольную величину, числа е и π;

- выполнять арифметические действия, сочетая устные и письменные приемы, применяя при необходимости вычислительные устройства;

- находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства;

- пользоваться оценкой и прикидкой при практических расчетах;

- проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, корни, логарифмы и тригонометрические функции;

- находить значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;

- изображать схематически угол, величина которого выражена в градусах или радианах;

- использовать при решении задач табличные значения тригонометрических функций углов;

- выполнять перевод величины угла из радианной меры в градусную и обратно.

- решать рациональные, показательные и логарифмические уравнения и неравенства, простейшие иррациональные и тригонометрические уравнения, неравенства и их системы;

- использовать методы решения уравнений: приведение к виду «произведение равно нулю» или «частное равно нулю», замена переменных;

- использовать метод интервалов для решения неравенств;

- использовать графический метод для приближенного решения уравнений и неравенств;

- изображать на тригонометрической окружности множество решений простейших тригонометрических уравнений и неравенств;

- выполнять отбор корней уравнений или решений неравенств в соответствии с дополнительными условиями и ограничениями.

- оперировать понятиями: зависимость величин, функция, аргумент и значение функции, область определения и множество значений функции, график зависимости, график функции, нули функции, промежутки знакопостоянства, возрастание на числовом промежутке, убывание на числовом промежутке, наибольшее и наименьшее значение функции на числовом промежутке, периодическая функция, период, четная и нечетная функции;

- оперировать понятиями: прямая и обратная пропорциональность, линейная, квадратичная, логарифмическая и показательная функции, тригонометрические функции;

- определять значение функции по значению аргумента при различных способах задания функции;

- строить графики изученных функций;

- описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;

- строить эскиз графика функции, удовлетворяющей приведенному набору условий (промежутки возрастания/убывания, значение функции в заданной точке, точки экстремумов, асимптоты, нули функции и т.д.);

- решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков.

- оперировать понятиями: производная функции в точке, касательная к графику функции, производная функции;

- вычислять производную одночлена, многочлена, квадратного корня, производную суммы функций;

- вычислять производные элементарных функций и их комбинаций, используя справочные материалы;

- исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов и простейших рациональных функций с использованием аппарата математического анализа.

- иметь представление о дискретных и непрерывных случайных величинах и распределениях, о независимости случайных величин;

- иметь представление о математическом ожидании и дисперсии случайных величин;

- иметь представление о нормальном распределении и примерах нормально распределенных случайных величин;

- понимать суть закона больших чисел и выборочного метода измерения вероятностей;

- иметь представление об условной вероятности и о полной вероятности, применять их в решении задач;

- иметь представление о важных частных видах распределений и применять их в решении задач;

- иметь представление о корреляции случайных величин, о линейной регрессии.

- решать задачи разных типов, в том числе задачи повышенной трудности;

- выбирать оптимальный метод решения задачи, рассматривая различные методы;

- строить модель решения задачи, проводить доказательные рассуждения;

- решать задачи, требующие перебора вариантов, проверки условий, выбора оптимального результата;

- анализировать и интерпретировать результаты в контексте условия задачи, выбирать решения, не противоречащие контексту;

- переводить при решении задачи информацию из одной формы в другую, используя при необходимости схемы, таблицы, графики, диаграммы;

- оперировать понятиями: точка, прямая, плоскость в пространстве, параллельность и перпендикулярность прямых и плоскостей;

- применять для решения задач геометрические факты, если условия применения заданы в явной форме;

- решать задачи на нахождение геометрических величин по образцам или алгоритмам;

- делать (выносные) плоские чертежи из рисунков объемных фигур, в том числе рисовать вид сверху, сбоку, строить сечения многогранников;

- извлекать, интерпретировать и преобразовывать информацию о геометрических фигурах, представленную на чертежах;

- применять геометрические факты для решения задач, в том числе предполагающих несколько шагов решения;

- описывать взаимное расположение прямых и плоскостей в пространстве;

- формулировать свойства и признаки фигур;

- доказывать геометрические утверждения;

- владеть стандартной классификацией пространственных фигур (пирамиды, призмы, параллелепипеды);

- находить объемы и площади поверхностей геометрических тел с применением формул;

- вычислять расстояния и углы в пространстве.

- оперировать понятиями декартовы координаты в пространстве, вектор, модуль вектора, равенство векторов, координаты вектора, угол между векторами, скалярное произведение векторов, коллинеарные векторы;

- находить расстояние между двумя точками, сумму векторов и произведение вектора на число, угол между векторами, скалярное произведение, раскладывать вектор по двум неколлинеарным векторам;

- задавать плоскость уравнением в декартовой системе координат;

- решать простейшие задачи введением векторного базиса.



В результате изучения математики на профильном уровне ученик должен:

Знать/понимать

-значение математической науки для решения задач, возникающих в теории и практике; широту и ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;

-значение практики и вопросов, возникающих в самой математике, для формирования и развития математической науки;

-значение практики и вопросов; возникающих в самой математике; для формирования и развития математической науки;

-значение идей; методов и результатов алгебры и математического анализа для построения моделей реальных процессов и ситуаций;

-возможности геометрии для описания свойств реальных предметов и их взаимного расположения;

-универсальный характер законов логики математических рассуждений; их

применимость в различных областях человеческой деятельности;

-роль аксиоматики в математике; возможность построения математических теорий на аксиоматической основе; значение аксиоматики для других областей знания и для практики;

-вероятностный характер различных процессов и закономерностей окружающего мира

Алгебра

Числовые и буквенные выражения

Уметь:

-выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значение корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;

-применять понятия, связанные с делимостью целых чисел, при решении математических задач;

-находить корни многочленов с одной переменной, раскладывать многочлены на множители;

-выполнять действия с комплексными числами, пользоваться геометрической интерпретацией комплексных чисел, находить комплексные корни уравнений с действительными коэффициентами;

-проводить преобразования числовых и буквенных выражений, включающих степени, радикалы, тригонометрические функции, логарифмы;

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

-практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства;

Функции и графики

У меть:

-определять значение функции по значению аргумента при различных способах задания функции;

-строить графики изученных функций, выполнять преобразования графиков;

-описывать по графику и по формуле поведение и свойства функций;

-решать уравнения, системы уравнений, неравенства, используя свойства функций и их графические представления;

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

-описания и исследования с помощью функций реальных зависимостей, представления их графически;

Начала математического анализа

Уметь:

-находить сумму бесконечно убывающей геометрической прогрессии;

-вычислять производные и первообразные элементарных функций, применяя правила вычисления производных и первообразных;

-исследовать функции и строить их графики с помощью производной;

-решать задачи с применением уравнения касательной к графику функции

-решать задачи на нахождение наибольшего и наименьшего значения функции на отрезке;

-вычислять площадь криволинейной трапеции;

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

-решения геометрических, физических, экономических и других прикладных задач, в том числе задач на наибольшие и наименьшие значения с применением аппарата математического анализа;

Уравнения и неравенства

Уметь:

-решать рациональные, показательные, логарифмические уравнения и неравенства, иррациональные и тригонометрические уравнения, их системы;

-доказывать несложные неравенства;

-решать текстовые задачи с помощью составления уравнений и неравенств, учитывая ограничения в условии задачи;

-изображать на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем; находить приближенные решения уравнений и их систем, используя графический метод;

- решать уравнения, неравенства и системы с применением графических представлений, свойств функций, производной;

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

-построения и исследования простейших математических моделей;

Элементы комбинаторики, статистики и теории вероятностей

Уметь:

-решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул, треугольника Паскаля; вычислять коэффициенты бинома Ньютона ;

-вычислять вероятности событий на основе подсчета числа исходов (простейшие случаи);

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

-анализа реальных числовых данных, представленных в виде диаграмм, графиков; для анализа информации статистического характера.


Геометрия

Уметь:

-соотносить плоские геометрические фигуры и трехмерные объекты с их описаниями, чертежами, изображениями; различать и анализировать взаимное расположение фигур;

-изображать геометрические фигуры тела, выполнять чертеж по условию задачи;

-решать геометрические задачи, опираясь на изученные свойства планиметрических и стереометрических фигур и отношений между ними;

-проводить доказательные рассуждения при решении задач, доказывать основные теоремы курса;

-вычислять линейные элементы и углы в пространственных конфигурациях, объемы и площади поверхностей пространственных тел и их простейших комбинаций;

-применять координатно-векторный метод для вычисления отношений, расстояний и углов;

-строить сечения многогранников и изображать сечения тел вращения.

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

-исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур;

-вычисление длин, площадей и объемов реальных объектов при решении практических задач, используя при необходимости справочники и вычислительные устройства.


Тематическое планирование: Математика: алгебра и начала математического анализа.

10 класс (базовый уровень).



№п/п

Название темы

(блок уроков)

Планируемые образовательные результаты

1

Повторение.

Личностные: формирование навыка осознанного выбора рационального способа решения заданий; формирование навыков самоанализа и самоконтроля; формирование навыка сотрудничества с учителем и сверстниками

Метопредметные:

Коммуникативные: организовывать и планировать учебное сотрудничество с учителем и одноклассниками; отстаивая свою точку зрения, приводить аргументы, подтверждая их фактами; в дискуссии уметь выдвинуть контраргументы;

Познавательные: строить логически обоснованное рассуждение, включающее установление причинно-следственных связей; анализировать, сравнивать, классифицировать и обобщать факты и явления;

Регулятивные: прогнозировать результат усвоения материала, определять промежуточные цели; самостоятельно обнаруживать и формулировать проблему в классной и индивидуальной учебной деятельности; уметь оценить степень успешности своей индивидуальной образовательной деятельности.

2

Числовые функции

Личностные: ответственное отношение к учению; умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи. Осуществлять взаимопроверку; обсуждать совместное решение (предлагать варианты, сравнивать способы вычисления или решения задачи); объединять полученные результаты; сопоставлять результаты собственной деятельности с оценкой её товарищами. Формирование интеллектуальной честности и объективности.

Метопредметные:

Коммуникативные: воспринимать текст с учетом поставленной учебной задачи, находить в тексте информацию, необходимую для ее решения; определять цели и функции участников, способы взаимодействия; планировать общие способы работы; обмениваться знаниями между членами группы для принятия эффективных совместных решений; аргументировать свою точку зрения, спорить и отстаивать свою позицию невраждебным для оппонентов образом; регулировать собственную деятельность посредством письменной речи.

Познавательные: выполнять учебные задачи, не имеющие однозначного решения; осуществлять сравнение и классификацию по заданным критериям; создавать структуру взаимосвязей смысловых единиц текста; выбирать наиболее эффективные способы решения задачи; уметь осуществлять анализ объектов, самостоятельно искать и отбирать необходимую информацию.

Регулятивные: самостоятельно находить и формулировать учебную проблему, составлять план выполнения работы; формировать целевые установки учебной деятельности, выстраивать последовательность необходимых операций.

Предметные:

Выпускник на базовом уровне научится:

- владеть понятиями: зависимость величин, функция, аргумент и значение функции, область определения и множество значений функции, график зависимости, график функции, нули функции, промежутки знакопостоянства, возрастание на числовом промежутке, убывание на числовом промежутке, наибольшее и наименьшее значение функции на числовом промежутке, четная и нечетная функции; и уметь применять эти понятия при решении задач;

- определять значение функции по значению аргумента при различных способах задания функции;

- строить графики изученных функций, выполнять преобразования графиков; описывать по графику и по формуле поведение и свойства функций; находить по графику функции наибольшее и наименьшее значения;

Выпускник на базовом уровне получит возможность научиться:

- научится описывать с помощью функций различные реальные зависимости между величинами и интерпретировать их графики;

- извлекать информацию, представленную в таблицах, на диаграммах, графиках.

3

Тригонометрические функции

Личностные: развитие интереса к математическому творчеству и математических способностей; формирование качеств мышления, необходимых для адаптации в современном информационном обществе; осуществлять самоконтроль, проверяя ответ на соответствие условию; готовность и способность обучающихся к саморазвитию и личностному самоопределению, способность ставить цели и строить жизненные планы; ответственное отношение к учению, развивать графическую культуру, образное мышление; развитие самостоятельности и критичности мышления; формирование интеллектуальной честности и объективности

Метапредметные:

Коммуникативные: определять цели и функции участников, способы взаимодействия; планировать общие способы работы; обмениваться знаниями между членами группы для принятия эффективных совместных решений; стабилизация эмоционального состояния для решения различных задач; понимая позицию другого, различать в его речи: мнение (точку зрения), доказательство (аргументы), факты; гипотезы, аксиомы, теории; обмениваться знаниями между одноклассниками для принятия эф­фективных совместных решений; уметь взглянуть на ситуацию с иной позиции и договариваться с людьми иных позиций.

Познавательные: осуществлять расширенный поиск информации с использованием ресурсов библиотеки, образовательного пространства родного края; выполнять учебные задачи, не имеющие однозначного решения; анализировать и осмысливать текст задачи;- моделировать условие с помощью схем, рисунков; строить логические рассуждения, умозаключения (индуктивные, дедуктивные и по аналогии) и выводы; - составлять тезисы, различные виды планов (простых, сложных и т.п.). Преобразовывать информацию из одного вида в другой (таблицу в текст, диаграмму и пр.); приводить примеры в ка­честве доказательства выдвигаемых положений; создавать математические модели; уметь использовать компьютерные и коммуникационные технологии как инструмент для достижения своих целей.

Регулятивные: формировать целевые установки учебной деятельности, выстраивать последовательность необходимых операций; самостоятельно находить и формулировать учебную проблему, составлять план выполнения работы; самостоятельно осознавать причины своего успеха или неуспеха и находить способы выхода из ситуации неуспеха; работая по предложенному или самостоятельно составленному плану, использовать наряду с основными и дополнительные средства (справочная литература, сложные приборы, компьютер); контроль и оценка деятельности; осуществлять итоговый и пошаговый контроль по результату; подбирать к каждой проблеме (задаче) адекватную ей теоретическую модель; уметь критически оценивать полученный ответ; предвидеть возможности получения конкретного результата при рациональном вычислениях; концентрация воли для преодоления интеллектуальных затруднений; работая по плану, сверять свои действия с целью и, при необходимости, исправлять ошибки самостоятельно (в том числе и корректировать план); уметь оценить степень успешности своей индивидуальной образовательной деятельности.

Предметные:

Выпускник на базовом уровне научится:

- владеть понятиями тригонометрические функции;

- строить их графики и уметь применять свойства тригонометрических функций при решении задач;

- переводить градусную меру в радианную и обратно;

- находить на окружности положение точки, соответствующей данному действительному числу;

- находить знаки значений синуса, косинуса, тангенса числа;

- выявлять зависимость между синусом, косинусом, тангенсом одного и того же угла.

Выпускник на базовом уровне получит возможность научиться:

- выполнять преобразования графиков элементарных функций: параллельный перенос, растяжение (сжатие) вдоль оси ординат;

- формулировать гипотезы о количестве корней уравнений, содержащих элементарные тригонометрические функции, и проверять их.

4

Тригонометрические уравнения

Личностные: чувство ответственности за выполнение своей части работы при работе в группе; умение признавать собственные ошибки; адекватная самооценка; формирование интеллектуальной честности и объективности. Развитие самостоятельности и критичности мышления. Формирование умений ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контпримеры; готовность к самообразованию и самовоспитанию. Воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения.

Метапредметные:

Коммуникативные: организовывать и планировать учебное сотрудничество с учителем и одноклассниками; проявлять готовность к обсуждению разных точек зрения и выработке общей (групповой) позиции; регулировать собственную деятельность посредством письменной речи; отстаивая свою точку зрения, приводить аргументы, подтверждая их фактами; в дискуссии уметь выдвинуть контраргументы; учиться критично относиться к своему мнению, с достоинством признавать ошибочность своего мнения (если оно таково) и корректировать его.

Познавательные: уметь осуществлять анализ объектов, самостоятельно искать и отбирать необходимую информацию; выбирать наиболее эффективные способы решения задачи; выявлять особенности (ка­чества, признаки) разных объектов в процессе их рассматривания; умение использовать приёмы решения задач; моделировать условие, строить логическую цепочку рассуждений; осуществлять контроль; умеют выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки; понимают и используют наглядность в решении учебных задач; отражение в письменной форме своих решений; осуществлять поиск необходимой информации для выполнения проблемных заданий с использованием учебной литературы.

Регулятивные: определять последовательность промежуточных целей с учетом конечного результата, составлять план последовательности действий; оценивать достигнутый результат; оценивать уровень владения учебным действием (отвечать на вопрос «что я не знаю и не умею?»); составлять (индивидуально или в группе) план решения проблемы (выполнения проекта); проявляют познавательный интерес к изучению предмета; уметь оценить степень успешности своей индивидуальной образовательной деятельности.

Предметные:

Выпускник на базовом уровне научится:

- уметь находить арксинус, арккосинус, арктангенс действительного числа, грамотно формулируя определение.

- применять формулы для нахождения корней уравнений cos х = а, sin x = a, tg х = а, ctg x = a

Выпускник на базовом уровне получит возможность научиться

- решать тригонометрические уравнения, сводящиеся к квадратным и другим алгебраическим уравнениям после замены неизвестного, сводящиеся к простейшим тригонометрическим уравнениям после разложения на множители.

- решать тригонометрические неравенства

5

Преобразование тригонометрических выражений

Личностные: формирование качеств мышления, необходимых для адаптации в современном информационном обществе; осуществлять самоконтроль, проверяя ответ на соответствие условию; развитие самостоятельности и критичности мышления. Формирование интеллектуальной честности и объективности.

Метапредметные:

Коммуникативные: организовывать и планировать учебное сотрудничество с учителем и одноклассниками; проявлять готовность к обсуждению разных точек зрения и выработке общей (групповой) позиции; способствовать формированию научного мировоззрения; слушать и понимать других, управлять поведением партнера, принимать точку зрения партнера.

Познавательные: уметь осуществлять анализ объектов, самостоятельно искать и отбирать необходимую информацию; самостоятельное выделение-формулирование познавательной цели; логические- формулирование проблемы, решение проблемы, построение логической цепи рассуждений; доказательство; рефлексия; умение структурировать знания, выбор наиболее эффективных способов решения задач, рефлексия способов и условий действия.

Регулятивные: определять последовательность промежуточных целей с учетом конечного результата, составлять план последовательности действий; целеполагание, планирование, прогнозирование, контроль, оценка, коррекция; формировать постановку учеб­ной задачи на основе соотнесения того, что уже известно и усвоено учащимися, и того, что еще неизвестно.

Предметные:

Выпускник на базовом уровне научится:

- доказывать основные тригонометрические тождества;

- использовать формулы приведения; синуса, косинуса и тангенса суммы и разности двух углов; синуса и косинуса двойного угла при преобразованиях простейших тригонометрических выражений.

Выпускник на базовом уровне получит возможность научиться:

- преобразовывать тригонометрические выражения различной сложности

- доказывать тождества, применяя различные методы, используя все изученные формулы

- применять все изученные свойства и формулы при решении прикладных задач

6

Производная

Личностные: развитие интереса к математическому творчеству и математических способностей; формирование качеств мышления, необходимых для адаптации в современном информационном обществе; осуществлять самоконтроль, проверяя ответ на соответствие условию; готовность и способность обучающихся к саморазвитию и личностному самоопределению, способность ставить цели и строить жизненные планы; ответственное отношение к учению, развивать графическую культуру, образное мышление; развитие самостоятельности и критичности мышления; формирование интеллектуальной честности и объективности

Метапредметные:

Коммуникативные: определять цели и функции участников, способы взаимодействия; планировать общие способы работы; обмениваться знаниями между членами группы для принятия эффективных совместных решений; стабилизация эмоционального состояния для решения различных задач; понимая позицию другого, различать в его речи: мнение (точку зрения), доказательство (аргументы), факты; гипотезы, аксиомы, теории; обмениваться знаниями между одноклассниками для принятия эф­фективных совместных решений; уметь взглянуть на ситуацию с иной позиции и договариваться с людьми иных позиций.

Познавательные: осуществлять расширенный поиск информации с использованием ресурсов библиотеки, образовательного пространства родного края; выполнять учебные задачи, не имеющие однозначного решения; анализировать и осмысливать текст задачи;- моделировать условие с помощью схем, рисунков; строить логические рассуждения, умозаключения (индуктивные, дедуктивные и по аналогии) и выводы; - составлять тезисы, различные виды планов (простых, сложных и т.п.). Преобразовывать информацию из одного вида в другой (таблицу в текст, диаграмму и пр.); приводить примеры в ка­честве доказательства выдвигаемых положений; создавать математические модели; уметь использовать компьютерные и коммуникационные технологии как инструмент для достижения своих целей.

Регулятивные: формировать целевые установки учебной деятельности, выстраивать последовательность необходимых операций; самостоятельно находить и формулировать учебную проблему, составлять план выполнения работы; самостоятельно осознавать причины своего успеха или неуспеха и находить способы выхода из ситуации неуспеха; работая по предложенному или самостоятельно составленному плану, использовать наряду с основными и дополнительные средства (справочная литература, сложные приборы, компьютер); контроль и оценка деятельности; осуществлять итоговый и пошаговый контроль по результату; подбирать к каждой проблеме (задаче) адекватную ей теоретическую модель; уметь критически оценивать полученный ответ; предвидеть возможности получения конкретного результата при рациональном вычислениях; концентрация воли для преодоления интеллектуальных затруднений; работая по плану, сверять свои действия с целью и, при необходимости, исправлять ошибки самостоятельно (в том числе и корректировать план); уметь оценить степень успешности своей индивидуальной образовательной деятельности.

Предметные:

Выпускник на базовом уровне научится:

- находить сумму бесконечно убывающей геометрической прогрессии; владеть понятиями: производная функции в точке, производная функции;

- вычислять производные элементарных функций, применяя правила вычисления производных, используя справочные материалы;

- решать задачи с применением уравнения касательной к графику функции;

- решать задачи на нахождение наибольшего и наименьшего значения функции на отрезке.

Выпускник на базовом уровне получит возможность научиться:

- Находить производную сложной функции y = f (kx + b).

- применять решения прикладных задач, в том числе задач на наибольшие и наименьшие значения с применением аппарата математического анализа

- исследовать функцию с помощью производной и строить её график

7

Итоговое повторение

Личностные: независимость и критичность мышления; воля и настойчивость в достижении цели; формирование ответственного отношения к учению, готовности и способности обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию. Формирование интеллектуальной честности и объективности

Метапредметные:

.Коммуникативные: организовывать и планировать учебное сотрудничество с учителем и одноклассниками; проявлять готовность к обсуждению разных точек зрения и выработке общей (групповой) позиции; способствовать формированию научного мировоззрения; слушать и понимать других, управлять поведением партнера, принимать точку зрения партнера.

Познавательные: уметь осуществлять анализ объектов, самостоятельно искать и отбирать необходимую информацию; самостоятельное выделение-формулирование познавательной цели; логические- формулирование проблемы, решение проблемы, построение логической цепи рассуждений; доказательство; рефлексия; умение структурировать знания, выбор наиболее эффективных способов решения задач, рефлексия способов и условий действия.

Регулятивные: определять последовательность промежуточных целей с учетом конечного результата, составлять план последовательности действий; целеполагание, планирование, прогнозирование, контроль, оценка, коррекция; формировать постановку учеб­ной задачи на основе соотнесения того, что уже известно и усвоено учащимися, и того, что еще неизвестно.

8

Итого


Математическое планирование Математика: геометрия. 10 класс (базовый уровень)

№ п/п

Название темы (блок уроков)

Планируемые образовательные результаты

  1. 1

Повторение

Личностные: формирование навыка осознанного выбора рационального способа решения заданий; формирование навыков самоанализа и самоконтроля; формирование навыка сотрудничества с учителем и сверстниками

Метопредметные:

Коммуникативные: организовывать и планировать учебное сотрудничество с учителем и одноклассниками; отстаивая свою точку зрения, приводить аргументы, подтверждая их фактами; в дискуссии уметь выдвинуть контраргументы;

Познавательные: строить логически обоснованное рассуждение, включающее установление причинно-следственных связей; анализировать, сравнивать, классифицировать и обобщать факты и явления;

Регулятивные: прогнозировать результат усвоения материала, определять промежуточные цели; самостоятельно обнаруживать и формулировать проблему в классной и индивидуальной учебной деятельности; уметь оценить степень успешности своей индивидуальной образовательной деятельности.

  1. 2

Введение. Аксиомы стереометрии и их следствия

Личностные:

Сформированность мировоззрения, соответствующего современному уровню развития науки и общественной практики.

Метапредметные:

Регулятивные:

целеполагание – формулировать и удерживать учебную задачу; преобразовывать практическую задачу в образовательную.

планирование – выбирать действия в соответствии с поставленной задачей и условиями ее реализации, определять общую цель и пути ее достижения; прогнозирование – предвосхищать результат.

Познавательные:

общеучебные – использовать общие приемы решения поставленных задач;

смысловое чтение, знаковосимвлические действия общеучебные – выбирать наиболее эффективные способы решения задач; контролировать и оценивать процесс в результате своей деятельности; осознанно строить сообщения в устной форме.

Коммуникативные: инициативное сотрудничество – ставить вопросы, обращаться за помощью; формулировать свои затруднения. проявлять активность во взаимодействии для решения задач; взаимодействие – задавать вопросы, формулировать свою позицию

Предметные:

Выпускник на базовом уровне научится:

- понимать аксиоматический способ построения геометрии, различать основные фигуры в пространстве, способы их обозначения, применять формулировки аксиом стереометрии их для решения простейших задач;

- соотносить плоские геометрические фигуры и трехмерные объекты с их описаниями, чертежами, изображениями;

- различать и анализировать взаимное расположение фигур;

- изображать геометрические фигуры и тела, выполнять чертеж по условию задачи.

Выпускник на базовом уровне получит возможность научиться:

- использовать аксиомы и следствия из них при решении задач логического характера;

- изображать точки, прямые и плоскости на проекционном чертеже при различном их взаимном расположении в пространстве.

  1. 3

Параллельность прямых и плоскостей

Личностные:

Бережное, ответственное и компетентное отношение к физическому и психологическому здоровью как собственному, так и других людей, умение оказывать первую помощь.

Метапредметные:

Регулятивные: целеполагание – преобразовывать практическую задачу в образовательную; формулировать и удерживать учебную задачу; удерживать познавательную задачу и применять установленные правила. контроль и самоконтроль – использовать

установленные правила в контроле способа решения задачи. планирование – выбирать действия в соответствии с поставленной задачей и условиями ее реализации.

Познавательные: общеучебные – выбирать наиболее эффективные решения поставленной задачи; контролировать и оценивать процесс и результат деятельности; ориентироваться в разнообразии программного обеспечения.

Коммуникативные: взаимодействие – формулировать собственное мнение и позицию; инициативное сотрудничество – ставить вопросы и обращаться за помощью; управление коммуникацией – осуществлять взаимный контроль; планирование

учебного сотрудничества – слушать собеседника, задавать вопросы; использовать речь.

Предметные:

Выпускник на базовом уровне научится:

- распознавать на чертежах и моделях пересекающиеся, параллельные прямые, пересекающие плоскость и параллельные ей; параллельные и пересекающиеся плоскости;

- решать геометрические задачи, опираясь на изученные свойства планиметрических и стереометрических фигур и отношений между ними, применяя алгебраический и геометрический аппарат;

- проводить доказательные рассуждения при решении задач;

- вычислять линейные элементы и углы в пространственных конфигурациях.

Выпускник на базовом уровне получит возможность научиться:

- доказывать основные теоремы курса

- научится изображать пространственные фигуры на плоскости в параллельной проекции.

  1. 4

Перпендикулярность прямых и плоскостей

Личностные:

Сформированность навыков сотрудничества со сверстниками, детьми младшего возраста, взрослыми в образовательной, общественно полезной, учебно-исследовательской, проектной и других видах деятельности.

Метапредметные:

Регулятивные: целеполагание – формулировать и удерживать учебную задачу; преобразовывать практическую

задачу в образовательную.

планирование – применять установленные правила в планировании способа решения;

коррекция – вносить необходимые коррективы в действие после его завершения на основе его оценки и учета сделанных ошибок; вносить необходимые дополнения и изменения в план и способ действия в случае расхождения действия и его результата; оценка – устанавливать соответствие полученного результата поставленной цели; коррекция – прогнозирование – предвидеть возможности получения конкретного результата при решении задач; контроль и самоконтроль – использовать установленные правила в контроле способа решения задачи.

Познавательные: общеучебные – ориентироваться в разнообразии программного обеспечения; осознанно строить сообщения в устной форме; ставить и формулировать проблемы; контролировать процесс и результат деятельности; – выбирать наиболее эффективные решения поставленной задачи; информационные – искать и выделять необходимую информацию из различных источников; получать и обрабатывать информацию.

Коммуникативные: планирование учебного сотрудничества – слушать собеседника, задавать вопросы определять общую цель и пути ее достижения;; использовать речь; инициативное сотрудничество – формулировать свои затруднения; взаимодействие – формулировать собственное мнение и позицию; строить для партнера понятные высказывания; строить для партнера понятные высказывания управление коммуникацией – адекватно использовать речь для планирования и регуляции своей деятельности;

Предметные:

Выпускник на базовом уровне научится:

- оперировать на базовом уровне понятиями: перпендикулярность прямых и плоскостей;

- изображать изучаемые фигуры от руки и с применением простых чертежных инструментов;

- извлекать информацию о пространственных геометрических фигурах, представленную на чертежах и рисунках;

- применять теорему Пифагора при вычислении элементов стереометрических фигур;

- применять для решения задач геометрические факты, если условия применения заданы в явной форме;

Выпускник на базовом уровне получит возможность научиться:

- - решать задачи на перпендикулярность прямых и плоскостей в пространстве, применять свойства перпендикулярных прямых и плоскостей.

- познакомится с понятием центрального проектирования и научится изображать пространственные фигуры на плоскости в центральной проекции.

  1. 5

Многогранники


Личностные:

готовность и способность к образованию, в том числе самообразованию, на протяжении всей жизни; сознательное отношение к непрерывному образованию как условию успешной профессиональной и общественной деятельности

Метапредметные:

Регулятивные: целеполагание – преобразовывать практическую задачу в образовательную;

контроль и самоконтроль – использовать установленные правила в контроле способа решения задачи; целеполагание – преобразовывать практическую задачу в образовательную; удерживать познавательную задачу и применять установленные правила;

коррекция – вносить необходимые коррективы в действие после его завершения на основе его оценки и учета сделанных ошибок.

Познавательные: общеучебные – выбирать наиболее эффективные решения поставленной задачи; контролировать и оценивать процесс и результат деятельности; ориентироваться в разнообразии способов решения задач; узнавать, называть и определять объекты и явления окружающей действительности в соответствии с содержанием учебного предмета.

Коммуникативные: взаимодействие – формулировать собственное мнение и позицию; управление коммуникацией – осуществлять взаимный контроль; формулировать свои затруднения.

Предметные:

Выпускник на базовом уровне научится:

- строить развертку;

- применять понятия: усеченная пирамида, наклонная призма;

- видеть симметрии в призме и пирамиде. Применить знания о симметрии в пространстве (центральная, осевая, зеркальная), приводить примеры симметрий в окружающем мире;

- решать стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объёмов); использовать при решении планиметрические факты и методы.

Выпускник на базовом уровне получит возможность научиться:

- владеть понятиями центральное и параллельное проектирование и применять их при построении сечений многогранников методом проекций;

- строить сечения многогранников; моделировать многогранники

  1. 6

Повторение

Личностные:

– принятие и реализация ценностей здорового и безопасного образа жизни, бережное, ответственное и компетентное отношение к собственному физическому и психологическому здоровью

Метапредметные:

Владение навыками познавательной рефлексии как осознания совершаемых действий и мыслительных процессов, их результатов и оснований, границ своего знания и незнания, новых познавательных задач и средств их достижения


Итого




Тематическое планирование: Математика: алгебра и начала математического анализа.

11 класс (базовый уровень).



№п/п

Название темы

(блок уроков)

Планируемые образовательные результаты

1

Повторение.

Личностные: сформированность мировоззрения, соответствующего современному уровню развития науки; критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;

формирование навыка осознанного выбора рационального способа решения заданий; формирование навыков самоанализа и самоконтроля; формирование навыка сотрудничества с учителем и сверстниками

Метопредметные:

Коммуникативные: организовывать и планировать учебное сотрудничество с учителем и одноклассниками; отстаивая свою точку зрения, приводить аргументы, подтверждая их фактами; в дискуссии уметь выдвинуть контраргументы;

Познавательные: строить логически обоснованное рассуждение, включающее установление причинно-следственных связей; анализировать, сравнивать, классифицировать и обобщать факты и явления;

Регулятивные: прогнозировать результат усвоения материала, определять промежуточные цели; самостоятельно обнаруживать и формулировать проблему в классной и индивидуальной учебной деятельности; уметь оценить степень успешности своей индивидуальной образовательной деятельности.

2

Степени и корни. Степенная функция.

Личностные: ответственное отношение к учению; умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи. Осуществлять взаимопроверку; обсуждать совместное решение (предлагать варианты, сравнивать способы вычисления или решения задачи); объединять полученные результаты; сопоставлять результаты собственной деятельности с оценкой её товарищами. Формирование интеллектуальной честности и объективности.

Метопредметные:

Коммуникативные: воспринимать текст с учетом поставленной учебной задачи, находить в тексте информацию, необходимую для ее решения; определять цели и функции участников, способы взаимодействия; планировать общие способы работы; обмениваться знаниями между членами группы для принятия эффективных совместных решений; аргументировать свою точку зрения, спорить и отстаивать свою позицию невраждебным для оппонентов образом; регулировать собственную деятельность посредством письменной речи.

Познавательные: выполнять учебные задачи, не имеющие однозначного решения; осуществлять сравнение и классификацию по заданным критериям; создавать структуру взаимосвязей смысловых единиц текста; выбирать наиболее эффективные способы решения задачи; уметь осуществлять анализ объектов, самостоятельно искать и отбирать необходимую информацию.

Регулятивные: самостоятельно находить и формулировать учебную проблему, составлять план выполнения работы; формировать целевые установки учебной деятельности, выстраивать последовательность необходимых операций.

Предметные:

Выпускник на базовом уровне научится:

- владеть понятием степенная функция; строить ее график и уметь применять свойства степенной функции при решении задач;

- различать функции y = n√x, их свойства и графики;

- решать простейшие иррациональные уравнения;

- оперировать степенью с действительным показателем.

Выпускник на базовом уровне получит возможность научиться:

- решать уравнения и неравенства, используя свойства функции и ее графическое представление

- распознавать равносильные преобразования, преобразования, приводящие к уравнению-следствию.

3

Показательная и логарифмическая функции

Личностные: развитие интереса к математическому творчеству и математических способностей; формирование качеств мышления, необходимых для адаптации в современном информационном обществе; осуществлять самоконтроль, проверяя ответ на соответствие условию; готовность и способность обучающихся к саморазвитию и личностному самоопределению, способность ставить цели и строить жизненные планы; ответственное отношение к учению, развивать графическую культуру, образное мышление; развитие самостоятельности и критичности мышления; формирование интеллектуальной честности и объективности

Метапредметные:

Коммуникативные: определять цели и функции участников, способы взаимодействия; планировать общие способы работы; обмениваться знаниями между членами группы для принятия эффективных совместных решений; стабилизация эмоционального состояния для решения различных задач; понимая позицию другого, различать в его речи: мнение (точку зрения), доказательство (аргументы), факты; гипотезы, аксиомы, теории; обмениваться знаниями между одноклассниками для принятия эф­фективных совместных решений; уметь взглянуть на ситуацию с иной позиции и договариваться с людьми иных позиций.

Познавательные: осуществлять расширенный поиск информации с использованием ресурсов библиотеки, образовательного пространства родного края; выполнять учебные задачи, не имеющие однозначного решения; анализировать и осмысливать текст задачи;- моделировать условие с помощью схем, рисунков; строить логические рассуждения, умозаключения (индуктивные, дедуктивные и по аналогии) и выводы; - составлять тезисы, различные виды планов (простых, сложных и т.п.). Преобразовывать информацию из одного вида в другой (таблицу в текст, диаграмму и пр.); приводить примеры в ка­честве доказательства выдвигаемых положений; создавать математические модели; уметь использовать компьютерные и коммуникационные технологии как инструмент для достижения своих целей.

Регулятивные: формировать целевые установки учебной деятельности, выстраивать последовательность необходимых операций; самостоятельно находить и формулировать учебную проблему, составлять план выполнения работы; самостоятельно осознавать причины своего успеха или неуспеха и находить способы выхода из ситуации неуспеха; работая по предложенному или самостоятельно составленному плану, использовать наряду с основными и дополнительные средства (справочная литература, сложные приборы, компьютер); контроль и оценка деятельности; осуществлять итоговый и пошаговый контроль по результату; подбирать к каждой проблеме (задаче) адекватную ей теоретическую модель; уметь критически оценивать полученный ответ; предвидеть возможности получения конкретного результата при рациональном вычислениях; концентрация воли для преодоления интеллектуальных затруднений; работая по плану, сверять свои действия с целью и, при необходимости, исправлять ошибки самостоятельно (в том числе и корректировать план); уметь оценить степень успешности своей индивидуальной образовательной деятельности.

Предметные:

Выпускник на базовом уровне научится:

- владеть понятиями показательная и логарифмическая функции; строить их графики и уметь применять свойства функций при решении задач.

- решать простейшие показательные уравнения, неравенства и их системы.

- решать показательные уравнения методами разложения на множители, способом замены неизвестного, с использованием свойств функции, решать уравнения, сводящиеся к квадратным.

- решать простейшие логарифмические уравнения, логарифмические неравенства и их системы.

Выпускник на базовом уровне получит возможность научиться:

- выполнять преобразования комбинированных логарифмических и показательных выражений;

- вычислять наибольшее и наименьшее значение показательной и логарифмической функций;

- применять свойства показательной функции при решении прикладных задач;

- формулировать гипотезы о количестве корней уравнений, содержащих логарифмическую функцию, и проверять их.

4

Первообразная и интеграл

Личностные: чувство ответственности за выполнение своей части работы при работе в группе; умение признавать собственные ошибки; адекватная самооценка; формирование интеллектуальной честности и объективности. Развитие самостоятельности и критичности мышления. Формирование умений ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контпримеры; готовность к самообразованию и самовоспитанию. Воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения.

Метапредметные:

Коммуникативные: организовывать и планировать учебное сотрудничество с учителем и одноклассниками; проявлять готовность к обсуждению разных точек зрения и выработке общей (групповой) позиции; регулировать собственную деятельность посредством письменной речи; отстаивая свою точку зрения, приводить аргументы, подтверждая их фактами; в дискуссии уметь выдвинуть контраргументы; учиться критично относиться к своему мнению, с достоинством признавать ошибочность своего мнения (если оно таково) и корректировать его.

Познавательные: уметь осуществлять анализ объектов, самостоятельно искать и отбирать необходимую информацию; выбирать наиболее эффективные способы решения задачи; выявлять особенности (ка­чества, признаки) разных объектов в процессе их рассматривания; умение использовать приёмы решения задач; моделировать условие, строить логическую цепочку рассуждений; осуществлять контроль; умеют выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки; понимают и используют наглядность в решении учебных задач; отражение в письменной форме своих решений; осуществлять поиск необходимой информации для выполнения проблемных заданий с использованием учебной литературы.

Регулятивные: определять последовательность промежуточных целей с учетом конечного результата, составлять план последовательности действий; оценивать достигнутый результат; оценивать уровень владения учебным действием (отвечать на вопрос «что я не знаю и не умею?»); составлять (индивидуально или в группе) план решения проблемы (выполнения проекта); проявляют познавательный интерес к изучению предмета; уметь оценить степень успешности своей индивидуальной образовательной деятельности.

Предметные:

Выпускник на базовом уровне научится:

- вычислять площади фигур на координатной плоскости с применением определённого интеграла.

Выпускник на базовом уровне получит возможность научиться:

- находить первообразные сложных функций f (kx + b).

- овладеть основными сведениями об интеграле Ньютона-Лейбница и его применениях.

5

Элементы теории вероятностей и математической статистики

Личностные: формирование качеств мышления, необходимых для адаптации в современном информационном обществе; осуществлять самоконтроль, проверяя ответ на соответствие условию; развитие самостоятельности и критичности мышления. Формирование интеллектуальной честности и объективности.

Метапредметные:

Коммуникативные: организовывать и планировать учебное сотрудничество с учителем и одноклассниками; проявлять готовность к обсуждению разных точек зрения и выработке общей (групповой) позиции; способствовать формированию научного мировоззрения; слушать и понимать других, управлять поведением партнера, принимать точку зрения партнера.

Познавательные: уметь осуществлять анализ объектов, самостоятельно искать и отбирать необходимую информацию; самостоятельное выделение-формулирование познавательной цели; логические- формулирование проблемы, решение проблемы, построение логической цепи рассуждений; доказательство; рефлексия; умение структурировать знания, выбор наиболее эффективных способов решения задач, рефлексия способов и условий действия.

Регулятивные: определять последовательность промежуточных целей с учетом конечного результата, составлять план последовательности действий; целеполагание, планирование, прогнозирование, контроль, оценка, коррекция; формировать постановку учеб­ной задачи на основе соотнесения того, что уже известно и усвоено учащимися, и того, что еще неизвестно.

Предметные:

Выпускник на базовом уровне научится:

- моделировать реальные ситуации на языке теории вероятностей и статистики, вычислять в простейших случаях вероятности событий;

- решать простейшие комбинаторные задачи методом перебора, а также с использованием известных формул, треугольника Паскаля;

Выпускник на базовом уровне получит возможность научиться:

- анализировать реальные числовые данные, информацию статистического характера;

-осуществлять практические расчеты по формулам;

- пользоваться оценкой и прикидкой при практических расчетах,

- вычислять коэффициенты бинома Ньютона по формуле и с использованием треугольника Паскаля.

6

Уравнения и неравенства. Системы уравнений и неравенств

Личностные: развитие интереса к математическому творчеству и математических способностей; формирование качеств мышления, необходимых для адаптации в современном информационном обществе; осуществлять самоконтроль, проверяя ответ на соответствие условию; готовность и способность обучающихся к саморазвитию и личностному самоопределению, способность ставить цели и строить жизненные планы; ответственное отношение к учению, развивать графическую культуру, образное мышление; развитие самостоятельности и критичности мышления; формирование интеллектуальной честности и объективности

Метапредметные:

Коммуникативные: определять цели и функции участников, способы взаимодействия; планировать общие способы работы; обмениваться знаниями между членами группы для принятия эффективных совместных решений; стабилизация эмоционального состояния для решения различных задач; понимая позицию другого, различать в его речи: мнение (точку зрения), доказательство (аргументы), факты; гипотезы, аксиомы, теории; обмениваться знаниями между одноклассниками для принятия эф­фективных совместных решений; уметь взглянуть на ситуацию с иной позиции и договариваться с людьми иных позиций.

Познавательные: осуществлять расширенный поиск информации с использованием ресурсов библиотеки, образовательного пространства родного края; выполнять учебные задачи, не имеющие однозначного решения; анализировать и осмысливать текст задачи;- моделировать условие с помощью схем, рисунков; строить логические рассуждения, умозаключения (индуктивные, дедуктивные и по аналогии) и выводы; - составлять тезисы, различные виды планов (простых, сложных и т.п.). Преобразовывать информацию из одного вида в другой (таблицу в текст, диаграмму и пр.); приводить примеры в ка­честве доказательства выдвигаемых положений; создавать математические модели; уметь использовать компьютерные и коммуникационные технологии как инструмент для достижения своих целей.

Регулятивные: формировать целевые установки учебной деятельности, выстраивать последовательность необходимых операций; самостоятельно находить и формулировать учебную проблему, составлять план выполнения работы; самостоятельно осознавать причины своего успеха или неуспеха и находить способы выхода из ситуации неуспеха; работая по предложенному или самостоятельно составленному плану, использовать наряду с основными и дополнительные средства (справочная литература, сложные приборы, компьютер); контроль и оценка деятельности; осуществлять итоговый и пошаговый контроль по результату; подбирать к каждой проблеме (задаче) адекватную ей теоретическую модель; уметь критически оценивать полученный ответ; предвидеть возможности получения конкретного результата при рациональном вычислениях; концентрация воли для преодоления интеллектуальных затруднений; работая по плану, сверять свои действия с целью и, при необходимости, исправлять ошибки самостоятельно (в том числе и корректировать план); уметь оценить степень успешности своей индивидуальной образовательной деятельности.

Предметные:

Выпускник на базовом уровне научится:

- свободно оперировать понятиями: уравнение, неравенство, равносильные уравнения, уравнение, являющееся следствием другого уравнения, уравнения, равносильные на множестве, равносильные преобразования уравнений;

- решать рациональные, иррациональные, показательные, тригонометрические и логарифмические уравнения, их системы, в том числе некоторые виды уравнений 3 и 4 степеней;

- решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков; использовать для приближенного решения уравнений и неравенств графический метод.

Выпускник на базовом уровне получит возможность научиться:

- свободно определять тип и выбирать метод решения показательных и логарифмических уравнений и неравенств иррациональных уравнений и неравенств, тригонометрических уравнений и неравенств, их систем;

- решать основные типы уравнений и неравенств с параметрами.

7

Итоговое повторение

Личностные: независимость и критичность мышления; воля и настойчивость в достижении цели; формирование ответственного отношения к учению, готовности и способности обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию. Формирование интеллектуальной честности и объективности

Метапредметные:

.Коммуникативные: организовывать и планировать учебное сотрудничество с учителем и одноклассниками; проявлять готовность к обсуждению разных точек зрения и выработке общей (групповой) позиции; способствовать формированию научного мировоззрения; слушать и понимать других, управлять поведением партнера, принимать точку зрения партнера.

Познавательные: уметь осуществлять анализ объектов, самостоятельно искать и отбирать необходимую информацию; самостоятельное выделение-формулирование познавательной цели; логические- формулирование проблемы, решение проблемы, построение логической цепи рассуждений; доказательство; рефлексия; умение структурировать знания, выбор наиболее эффективных способов решения задач, рефлексия способов и условий действия.

Регулятивные: определять последовательность промежуточных целей с учетом конечного результата, составлять план последовательности действий; целеполагание, планирование, прогнозирование, контроль, оценка, коррекция; формировать постановку учеб­ной задачи на основе соотнесения того, что уже известно и усвоено учащимися, и того, что еще неизвестно.

8

Итого






Математика: геометрия. 11 класс (базовый уровень)

№ п/п

Название темы (блок уроков)

Планируемые образовательные результаты

  1. 1

Повторение

Личностные: формирование навыка осознанного выбора рационального способа решения заданий; формирование навыков самоанализа и самоконтроля; формирование навыка сотрудничества с учителем и сверстниками

Метопредметные:

Коммуникативные: организовывать и планировать учебное сотрудничество с учителем и одноклассниками; отстаивая свою точку зрения, приводить аргументы, подтверждая их фактами; в дискуссии уметь выдвинуть контраргументы;

Познавательные: строить логически обоснованное рассуждение, включающее установление причинно-следственных связей; анализировать, сравнивать, классифицировать и обобщать факты и явления;

Регулятивные: прогнозировать результат усвоения материала, определять промежуточные цели; самостоятельно обнаруживать и формулировать проблему в классной и индивидуальной учебной деятельности; уметь оценить степень успешности своей индивидуальной образовательной деятельности.

  1. 2

Векторы в пространстве

Личностные:

Сформированность мировоззрения, соответствующего современному уровню развития науки и общественной практики.

Метапредметные:

Регулятивные:

целеполагание – формулировать и удерживать учебную задачу; преобразовывать практическую задачу в образовательную.

планирование – выбирать действия в соответствии с поставленной задачей и условиями ее реализации, определять общую цель и пути ее достижения; прогнозирование – предвосхищать результат.

Познавательные:

общеучебные – использовать общие приемы решения поставленных задач;

смысловое чтение, знаковосимвлические действия общеучебные – выбирать наиболее эффективные способы решения задач; контролировать и оценивать процесс в результате своей деятельности; осознанно строить сообщения в устной форме.

Коммуникативные: инициативное сотрудничество – ставить вопросы, обращаться за помощью; формулировать свои затруднения. проявлять активность во взаимодействии для решения задач; взаимодействие – задавать вопросы, формулировать свою позицию

Предметные:

Выпускник на базовом уровне научится:

- использовать известные из курса планиметрии сведения о векторах и действиях над ними, выполнять сложение, вычитание, умножение вектора на число;

- определять координаты точки; проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами.

Выпускник на базовом уровне получит возможность научиться:

- решать задачи на разложение вектора по трем некомпланарным векторам;

- решать геометрические задачи методом координат.

  1. 3

Метод координат в пространстве

Личностные:

Бережное, ответственное и компетентное отношение к физическому и психологическому здоровью как собственному, так и других людей, умение оказывать первую помощь.

Метапредметные:

Регулятивные: целеполагание – преобразовывать практическую задачу в образовательную; формулировать и удерживать учебную задачу; удерживать познавательную задачу и применять установленные правила. контроль и самоконтроль – использовать

установленные правила в контроле способа решения задачи. планирование – выбирать действия в соответствии с поставленной задачей и условиями ее реализации.

Познавательные: общеучебные – выбирать наиболее эффективные решения поставленной задачи; контролировать и оценивать процесс и результат деятельности; ориентироваться в разнообразии программного обеспечения.

Коммуникативные: взаимодействие – формулировать собственное мнение и позицию; инициативное сотрудничество – ставить вопросы и обращаться за помощью; управление коммуникацией – осуществлять взаимный контроль; планирование

учебного сотрудничества – слушать собеседника, задавать вопросы; использовать речь.

Предметные:

Выпускник на базовом уровне научится:

- использовать формулы скалярного произведения векторов, длины отрезка, координат середины отрезка при решении задач.

- строить точки по их координатам, находят координаты векторов. Находить угол между векторами, вычисляют угол между прямыми.

Выпускник на базовом уровне получит возможность научиться:

- выполнять построение фигуры, симметричной относительно оси симметрии, центра симметрии, плоскости, при параллельном переносе.

- применять координатно-векторный метод для вычисления отношений, расстояний и углов.

  1. 4

Цилиндр, конус, шар

Личностные:

Сформированность навыков сотрудничества со сверстниками, детьми младшего возраста, взрослыми в образовательной, общественно полезной, учебно-исследовательской, проектной и других видах деятельности.

Метапредметные:

Регулятивные: целеполагание – формулировать и удерживать учебную задачу; преобразовывать практическую

задачу в образовательную.

планирование – применять установленные правила в планировании способа решения;

коррекция – вносить необходимые коррективы в действие после его завершения на основе его оценки и учета сделанных ошибок; вносить необходимые дополнения и изменения в план и способ действия в случае расхождения действия и его результата; оценка – устанавливать соответствие полученного результата поставленной цели; коррекция – прогнозирование – предвидеть возможности получения конкретного результата при решении задач; контроль и самоконтроль – использовать установленные правила в контроле способа решения задачи.

Познавательные: общеучебные – ориентироваться в разнообразии программного обеспечения; осознанно строить сообщения в устной форме; ставить и формулировать проблемы; контролировать процесс и результат деятельности; – выбирать наиболее эффективные решения поставленной задачи; информационные – искать и выделять необходимую информацию из различных источников; получать и обрабатывать информацию.

Коммуникативные: планирование учебного сотрудничества – слушать собеседника, задавать вопросы определять общую цель и пути ее достижения;; использовать речь; инициативное сотрудничество – формулировать свои затруднения; взаимодействие – формулировать собственное мнение и позицию; строить для партнера понятные высказывания; строить для партнера понятные высказывания управление коммуникацией – адекватно использовать речь для планирования и регуляции своей деятельности;

Предметные:

Выпускник на базовом уровне научится:

- формулировать основные понятия, свойства, признаки и теоремы раздела.

- вычислять площади боковой и полной поверхности цилиндра, конуса, шара.

- выполнять чертежи по условию задачи, строить сечения

Выпускник на базовом уровне получит возможность научиться:

- воспроизводить вывод и доказательство основных формул и теорем.

- решать геометрические задачи, опираясь на изученные свойства планиметрических и стереометрических фигур и отношений между ними, применяя алгебраический и тригонометрический аппарат;

- строить сечения многогранников и изображать сечения тел вращения.

  1. 5

Объемы тел

Личностные:

готовность и способность к образованию, в том числе самообразованию, на протяжении всей жизни; сознательное отношение к непрерывному образованию как условию успешной профессиональной и общественной деятельности

Метапредметные:

Регулятивные: целеполагание – преобразовывать практическую задачу в образовательную;

контроль и самоконтроль – использовать установленные правила в контроле способа решения задачи; целеполагание – преобразовывать практическую задачу в образовательную; удерживать познавательную задачу и применять установленные правила;

коррекция – вносить необходимые коррективы в действие после его завершения на основе его оценки и учета сделанных ошибок.

Познавательные: общеучебные – выбирать наиболее эффективные решения поставленной задачи; контролировать и оценивать процесс и результат деятельности; ориентироваться в разнообразии способов решения задач; узнавать, называть и определять объекты и явления окружающей действительности в соответствии с содержанием учебного предмета.

Коммуникативные: взаимодействие – формулировать собственное мнение и позицию; управление коммуникацией – осуществлять взаимный контроль; формулировать свои затруднения.

Предметные:

Выпускник на базовом уровне научится:

- вычислять объем прямоугольного параллелепипеда, прямой призмы, цилиндра, наклонной призмы, пирамиды, конуса, шара, шарового сегмента, шарового слоя и шарового сектора.

Выпускник на базовом уровне получит возможность научиться:

- воспроизводить вывод и доказательство основных формул и теорем.

- вычислять линейные элементы и углы в пространственных конфигурациях, объемы и площади поверхностей пространственных тел и их простейших комбинаций.

  1. 6

Повторение

Личностные:

– принятие и реализация ценностей здорового и безопасного образа жизни, бережное, ответственное и компетентное отношение к собственному физическому и психологическому здоровью

Метапредметные:

Владение навыками познавательной рефлексии как осознания совершаемых действий и мыслительных процессов, их результатов и оснований, границ своего знания и незнания, новых познавательных задач и средств их достижения

  1. Содержание тем учебного предмета


Алгебра и начала анализа

Многочлены (10 ч)

Многочлены от одной и нескольких переменных. Теорема Безу. Схема Горнера. Симметрические и однородные многочлены. Уравнения высших степеней.



Степени и корни. Степенные функции (24 ч)_

Понятие корня n-ой степени из действительного числа. Функции y=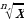 , их свойства и графики. Свойства корня n-ой степени. Преобразование выражений, содержащих радикалы. Обобщение понятия о показателе степени. Степенные функции, их свойства и графики. Дифференцирование и интегрирование. Извлечение корней n-ой степени из комплексных чисел.



Показательная и логарифмическая функции (31 ч)

: Показательная функция, её свойства и график. Показательные уравнения и неравенства. Понятие логарифма. Функция y=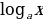 , её свойства и график. Свойства логарифмов. Логарифмические уравнения и неравенства. Дифференцирование показательной и логарифмической функций.



Интеграл (9 ч)

Первообразная и неопределённый интеграл. Определённый интеграл, его вычисление и свойства. Вычисление площадей плоских фигур. Примеры применения интеграла в физике.



Элементы комбинаторики, статистики и теории вероятностей (9 ч)

Вероятность и геометрия. Независимые повторения испытаний с двумя исходами. Статистические методы обработки информации. Гауссова кривая. Закон больших чисел.



Уравнения и неравенства. Системы уравнений и неравенств (33 ч)

Равносильность уравнений. Общие методы решения уравнений. Уравнения с модулями. Иррациональные уравнения. Доказательство неравенств. Решение рациональных неравенств с одной переменной. Неравенства с модулями. Иррациональные неравенства. Уравнения и неравенства с двумя переменными. Диофантовы уравнения. Системы уравнений. Уравнения и неравенства с параметрами.



Обобщающее повторение (16 ч)






Геометрия


Векторы в пространстве (6 ч)

Понятие вектора в пространстве. Сложение и вычитание векторов. Умножение вектора на число. Компланарные векторы.

Основная цель — закрепить известные учащимся из курса планиметрии сведения о векторах и действиях над ними, ввести понятие компланарных векторов в простран­стве и рассмотреть вопрос о разложении любого вектора по трем данным некомпланарным векторам.

Основные определения, относящиеся к действиям над векторами в пространстве, вводятся так же, как и для векторов на плоскости. Поэтому изложение этой части материала является достаточно сжатым. Более подробно рассматриваются вопросы, характерные для векторов в пространстве: компланарность векторов, правило паралле­лепипеда сложения трех некомпланарных векторов, разло­жение вектора по трем некомпланарным векторам.



Метод координат в пространстве (15 ч)

Координаты точки и координаты вектора. Скалярное произведение векторов. Движения Уравнение плоскости. Преобразование подобия.

Основная цель — сформировать умение учащихся применять векторно-координатный метод к решению задач на вычисление углов между прямыми и плоскостями и рас­стояний между двумя точками, от точки до плоскости.

Данный раздел является непосредственным продолже­нием предыдущего. Вводится понятие прямоугольной си­стемы координат в пространстве, даются определения ко­ординат точки и координат вектора, рассматриваются простейшие задачи в координатах. Затем вводится ска­лярное произведение векторов, кратко перечисляются его свойства (без доказательства, поскольку соответствующие доказательства были в курсе планиметрии) и выводятся формулы для вычисления углов между двумя прямыми, между прямой и плоскостью. Дан также вывод уравне­ния плоскости и формулы расстояния от точки до плос­кости.

В конце раздела изучаются движения в пространстве: центральная симметрия, осевая симметрия, зеркальная симметрия. Кроме того, рассмотрено преобразование подо­бия.



Цилиндр, конус, шар (16 ч)

Понятие цилиндра. Площадь поверхности цилиндра. Понятие конуса. Площадь поверхности конуса. Усеченный конус. Сфера и шар. Уравнение сферы. Взаимное располо­жение сферы и плоскости. Касательная плоскость к сфере. Площадь сферы.

Основная цель — дать учащимся систематические сведения об основных телах и поверхностях вращения — цилиндре, конусе, сфере, шаре.

Изучение круглых тел (цилиндра, конуса, шара) и их поверхностей завершает знакомство учащихся с основными пространственными фигурами. Вводятся понятия цилинд­рической и конической поверхностей, цилиндра, конуса, усеченного конуса. С помощью разверток определяются площади их боковых поверхностей, выводятся соответству­ющие формулы. Затем даются определения сферы и шара, выводится уравнение сферы и с его помощью исследуется вопрос о взаимном расположении сферы и плоскости. Пло­щадь сферы определяется как предел последовательности площадей описанных около сферы многогранников при стремлении к нулю наибольшего размера каждой грани. В задачах рассматриваются различные комбинации круг­лых тел и многогранников, в частности описанные и впи­санные призмы и пирамиды.

В данном разделе изложены также вопросы о взаимном расположении сферы и прямой, о сечениях цилиндрической и конической поверхностей различными плоскостями.



Объемы тел (17 ч)

Объем прямоугольного параллелепипеда. Объемы пря­мой призмы и цилиндра. Объемы наклонной призмы, пи­рамиды и конуса. Объем шара и площадь сферы. Объемы шарового сегмента, шарового слоя и шарового сектора.

Основная цель — ввести понятие объема тела и выве­сти формулы для вычисления объемов основных многогран­ников и круглых тел, изученных в курсе стереометрии.

Понятие объема тела вводится аналогично понятию пло­щади плоской фигуры. Формулируются основные свойства объемов, и на их основе выводится формула объема пря­моугольного параллелепипеда, а затем прямой призмы и цилиндра. Формулы объемов других тел выводятся с по­мощью интегральной формулы. Формула объема шара ис­пользуется для вывода формулы площади сферы.

Заключительное повторение 14 ч

Содержание учебного предмета

Числовые функции (10кл)

Определение числовой функции и способы ее задания. Свойства функций. Обратные функции.

§ 7. Определение числовой функции и способы ее задания

§ 8. Свойства функций

§ 10. Обратная функция

Тригонометрические функции (10кл)

Числовая окружность на координатной плоскости. Определение синуса, косинуса, тангенса и котангенса. Тригонометрические функции числового и углового аргумента, их свойства и графики. Сжатие и растяжение графиков тригонометрических функций. Обратные тригонометрические функции.

§ 11. Числовая окружность

§ 12. Числовая окружность на координатной плоскости

§ 13. Синус и косинус. Тангенс и котангенс

1. Синус и косинус

2. Тангенс и котангенс

§ 14. Тригонометрические функции числового аргумента

§ 15. Тригонометрические функции углового аргумента

§ 16. Функции у = sin х, у = cos х, их свойства и графики

1. Функция у = sin х

2. Функция у = cos х

§ 17. Построение графика функции у = mf(x)

§ 18. Построение графика функции у = f(kx)

§ 20. Функции у = tg х, у = ctg х, их свойства и графики

§ 21. Обратные тригонометрические функции

1. Функция у = arcsin x

2. Функция у = arccos x

3. Функция у = arctg x

4. Функция у = arcctg x

Тригонометрические уравнения и неравенства (10кл)

Простейшие тригонометрические уравнения и неравенства. Методы решения тригонометрических уравнений: метод замены переменной, метод разложения на множители, однородные тригонометрические уравнения.

§ 22. Простейшие тригонометрические уравнения и неравенства

1. Первые представления о простейших тригонометрических уравнениях

2. Решение уравнения cos t = a

3. Решение уравнения sin t = a

4. Решение уравнений tg х = a, ctg х = а

5. Простейшие тригонометрические уравнения

§ 23. Методы решения тригонометрических уравнений

1. Метод замены переменной

2. Метод разложения на множители

3. Однородные тригонометрические уравнения

Преобразование тригонометрических выражений (10кл)

Формулы сложения, приведения, двойного аргумента, понижения степени. Преобразование суммы тригонометрических функций в произведение и произведения в сумму.

§ 24. Синус и косинус суммы и разности аргументов

§ 25. Тангенс суммы и разности аргументов

§ 26. Формулы приведения

§ 27. Формулы двойного аргумента.

Формулы понижения степени

§ 28. Преобразование сумм тригонометрических функций в произведения

§ 29. Преобразование произведений тригонометрических функций в суммы

Производная (10кл)

Определение числовой последовательности, способы ее задания и свойства. Предел числовой последовательности, свойства сходящихся последовательностей. Сумма бесконечной геометрической прогрессии. Предел функции на бесконечности и в точке.

Задачи, приводящие к понятию производной, определение производной,

вычисление производных. Понятие производной n-го порядка. Уравнение касательной к графику функции. Применение производной для исследования функций на монотонность и экстремумы. Применение производной для доказательства тождеств и неравенств.

§ 37. Числовые последовательности

1. Определение числовой последовательности и способы ее задания

2. Свойства числовых последовательностей

§ 38. Предел числовой последовательности

1. Определение предела последовательности

2. Свойства сходящихся последовательностей

3. Вычисление пределов последовательностей

§ 39. Предел функции

1. Предел функции на бесконечности

2. Предел функции в точке

3. Приращение аргумента. Приращение функции

§ 40. Определение производной

1. Задачи, приводящие к понятию производной

2. Определение производной

§ 41. Вычисление производных

1. Формулы дифференцирования

2. Правила дифференцирования

3. Понятие и вычисление производной п-го порядка

§ 43. Уравнение касательной к графику функции

§ 44. Применение производной для исследования функций

1. Исследование функций на монотонность

2. Отыскание точек экстремума

Степени и корни. Степенные функции (11кл)

Понятие корня n-й степени из действительного числа. Функции , их свойства и графики. Свойства корня n-й степени. Преобразование выражений, содержащих радикалы. Обобщение понятия о показателе степени. Степенные функции, их свойства и графики (включая дифференцирование и интегрирование).

§ 4. Понятие корня n-й степени из действительного числа

§ 5. Функции у - yjx, их свойства и графики

§ 6. Свойства корня n-й степени

§ 7. Преобразование иррациональных выражений

§ 8. Понятие степени с любым рациональным показателем

§ 9. Степенные функции, их свойства и графики

Показательная и логарифмическая функции (11кл)

Показательная функция, ее свойства и график. Показательные уравнения и не- равенства. Понятие логарифма. Функция , ее свойства и график. Свойства логарифмов. Логарифмические уравнения и неравенства. Дифференирование показательной и логарифмической функций.

§ 11. Показательная функция, её свойства и график

§ 12. Показательные уравнения

§ 13. Показательные неравенства

§ 14. Понятие логарифма

§ 15. Логарифмическая функция, её свойства и график

§ 16. Свойства логарифмов

§ 17. Логарифмические уравнения

§ 18. Логарифмические неравенства

§ 19. Дифференцирование показательной и логарифмической функций

Первообразная и интеграл (11кл)

Первообразная и интеграл. Определенный интеграл, его вычисление и свойства. Вычисление площадей плоских фигур.

§ 20. Первообразная и неопределённый интеграл 155

§ 21. Определённый интеграл 165

Элементы комбинаторики, статистики и теории вероятности (11кл)

Вероятность и геометрия. Независимые повторения испытаний с двумя исходами. Статистические методы обработки информации.

§ 22. Вероятность и геометрия

§ 23. Независимые повторения испытаний с двумя исходами

§ 24. Статистические методы обработки информации

Уравнения и неравенства. Системы уравнений и неравенств (11кл)

Равносильность уравнений. Общие методы решения уравнений. Уравнения с модулями. Иррациональные уравнения. Доказательство неравенств. Решение рациональных неравенств с одной переменной. Иррациональные неравенства. Уравнения и неравенства с двумя переменными. Диофантовы уравнения. Системы уравнений.

§ 26. Равносильность уравнений

§ 27. Общие методы решения уравнений

§ 28. Равносильность неравенств

§ 30. Иррациональные уравнения и неравенства

§ 31. Доказательство неравенств

§ 32. Уравнения и неравенства с двумя переменными

§ 33. Системы уравнений

Введение (10кл)

Основные понятия стереометрии (точка, прямая, плоскость, пространство) и аксиомы стереометрии. Первые следствия из аксиом.

1. Предмет стереометрии

2. Аксиомы стереометрии

3. Некоторые следствия из аксиом

Параллельность прямых и плоскостей (10кл)

Пересекающиеся, параллельные и скрещивающиеся прямые. Параллельность прямой и плоскости, признак и свойства. Угол между прямыми в пространстве. Перпендикулярность прямых. Параллельность плоскостей, признаки и свойства. Параллельное проектирование. Изображение пространственных фигур. Тетраэдр и параллелепипед, куб. Сечения куба, призмы, пирамиды.

§ 1. Параллельность прямых, прямой и плоскости

4. Параллельные прямые в пространстве

5. Параллельность трех прямых

6. Параллельность прямой и плоскости

§ 2. Взаимное расположение прямых в пространстве. Угол между двумя прямыми

7. Скрещивающиеся прямые

8. Углы с сонаправленными сторонами

9. Угол между прямыми

§ 3. Параллельность плоскостей

10. Параллельные плоскости

11. Свойства параллельных плоскостей

§ 4. Тетраэдр и параллелепипед

12. Тетраэдр

13. Параллелепипед

14. Задачи на построение сечений

Перпендикулярность прямых и плоскостей (10кл)

Перпендикулярность прямой и плоскости, признаки и свойства. Перпендикуляр и наклонная. Теорема о трех перпендикулярах. Угол между прямой и плоскостью. Расстояние от точки до плоскости. Расстояние от прямой до плоскости. Расстояние между параллельными плоскостями. Расстояние между скрещивающимися прямыми. Перпендикулярность плоскостей, признаки и свойства. Двугранный угол, линейный угол двугранного угла. Площадь ортогональной проекции многоугольника.

§ 1. Перпендикулярность прямой и плоскости

15. Перпендикулярные прямые в пространстве

16. Параллельные прямые, перпендикулярные к плоскости .

17. Признак перпендикулярности прямой и плоскости

18. Теорема о прямой, перпендикулярной к плоскости

§ 2. Перпендикуляр и наклонные. Угол между прямой и плоскостью

19. Расстояние от точки до плоскости

20. Теорема о трех перпендикулярах

21. Угол между прямой и плоскостью

§ 3. Двугранный угол. Перпендикулярность плоскостей

22. Двугранный угол

23. Признак перпендикулярности двух плоскостей

24. Прямоугольный параллелепипед

Многогранники (10кл)

Понятие многогранника, вершины, ребра, грани многогранника. Развертка. Многогранные углы Выпуклые многогранники. Призма, ее основание, боковые ребра, высота, боковая и полная поверхности.

Прямая и наклонная призма. Правильная призма. Пирамида, ее основание, боковые ребра, высота, боковая и полная поверхности. Треугольная пирамида. Правильная пирамида. Усеченная пирамида. Симметрия в кубе, в параллелепипеде, в призме и пирамиде. Понятие о симметрии в пространстве (центральная, осевая и зеркальная). Примеры симметрий в окружающем мире. Представление о правильных многогранниках (тетраэдр, куб, октаэдр, додекаэдр и икосаэдр).

§ 1. Понятие многогранника. Призма

27. Понятие многогранника

30. Призма

§ 2. Пирамида

32. Пирамида

33. Правильная пирамида

34. Усеченная пирамида

§ 3. Правильные многогранники

35. Симметрия в пространстве

36. Понятие правильного многогранника

37. Элементы симметрии правильных многогранников

Векторы к пространстве (11кл)

Понятие вектора в пространстве. Модуль вектора. Равенство векторов. Сложение и вычитание векторов. Коллинеарные векторы. Умножение вектора на число. Разложение вектора по двум неколлинеарным векторам. Компланарные векторы. Разложение вектора по трем некомпланарным векторам.

§ 1. Понятие вектора в пространстве

38. Понятие вектора

39. Равенство векторов

§ 2. Сложение и вычитание векторов. Умножение вектора на число

40. Сложение и вычитание векторов

41. Сумма нескольких векторов

42. Умножение вектора на число

§ 3. Компланарные векторы

43. Компланарные векторы

44. Правило параллелепипеда

45. Разложение вектора по трем некомпланарным векторам

Метод координат в пространств. Движения (11кл)

Декартовы координаты в пространстве. Формула расстояния между двумя точками. Формула расстояния от точки до плоскости.

Векторы. Угол между векторами. Координаты вектора. Скалярное произведение векторов. Длина вектора в координатах, угол между векторами в координатах. Коллинеарные векторы, коллинеарность векторов в координатах.

§ 1. Координаты точки и координаты вектора

46. Прямоугольная система координат в пространстве

47. Координаты вектора

48. Связь между координатами векторов и координатами точек .

49. Простейшие задачи в координатах

§ 2. Скалярное произведение векторов

50. Угол между векторами

51. Скалярное произведение векторов

52. Вычисление углов между прямыми и плоскостями

§ 3. Движения

54. Центральная симметрия

55. Осевая симметрия

56. Зеркальная симметрия

57. Параллельный перенос

Цилиндр, конус, шар (11кл)

Цилиндр и конус. Усеченный конус. Основание, высота, боковая поверхность, образующая, развертка. Осевые сечения и сечения параллельные основанию.

Шар и сфера, их сечения, касательная плоскость к сфере.

§ 1. Цилиндр

59. Понятие цилиндра

60. Площадь поверхности цилиндра

§ 2. Конус

61. Понятие конуса

62. Площадь поверхности конуса

63. Усеченный конус

§ 3. Сфера

64. Сфера и шар

65. Уравнение сферы

66. Взаимное расположение сферы и плоскости

67. Касательная плоскость к сфере

68. Площадь сферы

Объемы тел (11кл)

Понятие об объеме тела. Отношение объемов подобных тел.

Формулы объема куба, прямоугольного параллелепипеда, призмы, цилиндра. Формулы объема пирамиды и конуса. Формулы площади поверхностей цилиндра и конуса. Формула объема шара.

§ 1. Объем прямоугольного параллелепипеда

74. Понятие объема

75. Объем прямоугольного параллелепипеда

§ 2. Объемы прямой призмы и цилиндра

76. Объем прямой призмы

77. Объем цилиндра

§ 3. Объемы наклонной призмы, пирамиды и конуса

78. Вычисление объемов тел с помощью интеграла

79. Объем наклонной призмы

80. Объем пирамиды

81. Объем конуса

§ 4. Объем шара и площадь сферы

82. Объем шара

83. Объемы шарового сегмента, шарового слоя и шарового сектора




Математика 6 класс

Алгебра 8 класс ФГОС

Наглядная геометрия 5-6 классы ФГОС

Математика 6 класс ФГОС

Математика и игры в средней школе

Геометрия 11 класс ФГОС

Электронная тетрадь по геометрии 7...

Алгебра 11 класс ФГОС
Скачать

© 2021, 121 0

Похожие файлы

0 Нет комментариев

Вебинар для учителей

Свидетельство об участии БЕСПЛАТНО!

Полезное для учителя

Новости проекта
03.06.24

Лайфхак учителя №1! Что делать с плохой накопляемостью отметок

12.05.24

Лайфхак учителя №2! Как перестать бегать от ученика к ученику во время практической работы

04.05.24

Лайфхак учителя №3! Что делать, если вы устали из урока в урок повторять одно и то же