Лекция "Работа с графами"

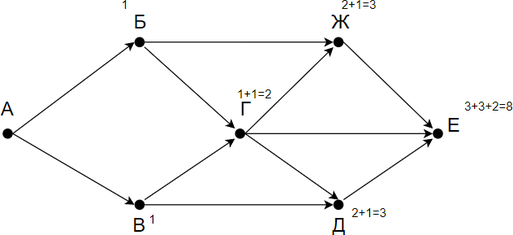
Простейшие задачи на графы Задание 1 #12575 На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Е?

Показать решение

Заметим, что количество путей в город Е является суммой путей в города Ж, Г и Д. Количество путей в город Ж — сумма путей в города Г и Б. Таким образом получаем: Г = Б + В Д = Г + В Ж = Б + Г Е = Ж + Г + Д Заметим, что в пункты Б и В можно попасть единственным способом — из города А. Отметим на рисунке индексами сверху каждого пункта количество путей, с помощью которых в него можно попасть и посчитаем итоговое.

Ответ: 8

ответ 8

На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город Ж?

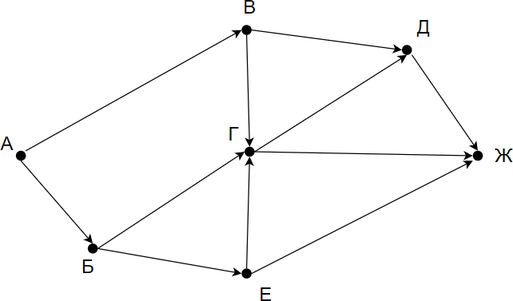
Заметим, что количество путей в город Ж является суммой путей в города Д, Г и Е. Количество путей в город Г — сумма путей в город В, Б и Е. Таким образом получаем: Г = Б + В + Е Д = В + Г Ж = Д + Г + Е Заметим, что в пункты Б, В и Е можно попасть единственным способом — из города А. Отметим на рисунке индексами сверху каждого пункта количество путей, с помощью которых в него можно попасть и посчитаем итоговое.

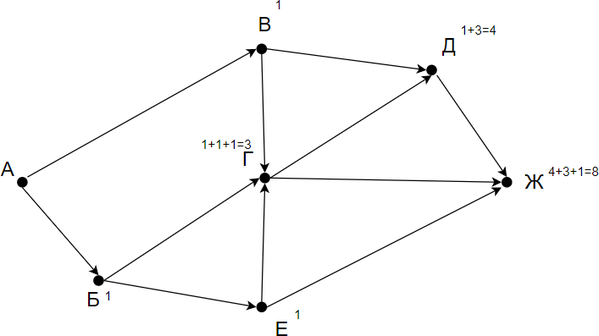
Ответ 8

Между населёнными пунктами А, В, С, D, Е построены дороги, протяжённость которых (в километрах) приведена в таблице:

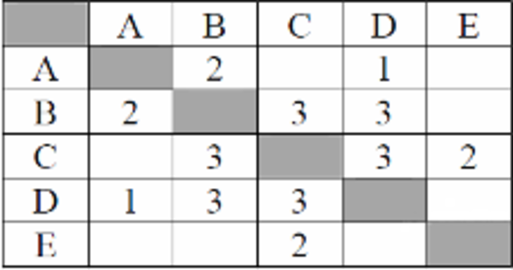
Найдём все варианты маршрутов из A в E и выберем самый короткий. Из пункта A можно попасть в пункты B, D. Из пункта B можно попасть в пункты C, D. Из пункта C можно попасть в пункты D, E. A—B—C—E: длина маршрута 7 км. A—D—B—C—E: длина маршрута 9 км. A—D—C—E: длина маршрута 6 км. Самый короткий путь: A—D—C—E. Длина маршрута 6 км. Ответ: 6

_______________________________________________________

Геральт спешит выручить Цири из плена Кагыра. В таблице указана протяжённость дорог между пунктами, через которые он может пройти. Укажите длину самого короткого участка кратчайшего пути от Геральта до Цири (от точки И до точки М). Передвигаться можно только по дорогам, указанным в таблице:

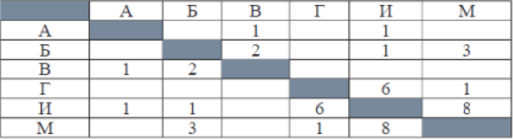
Найдём все варианты маршрутов из И в М и выберем самый короткий. Из пункта И можно попасть в пункты А, Б, Г, М. Из пункта Г можно попасть в пункты И, М. Из пункта В можно попасть в пункты А, Б. Из пункта Б можно попасть в пункты В, И, М. И—А—В—Б—М: длина маршрута 7 км. И—Б—М: длина маршрута 4 км. И—Г—М: длина маршрута 7 км. И—М: длина маршрута 8 км. Самый короткий путь: И—Б—М. Длина маршрута 4 км. Самый короткий участок этого пути равен 1 км. Ответ: 1

___________________________________

На схеме нарисованы дороги между четырьмя населёнными пунктами A, B, C, D и указаны протяжённости данных дорог. Определите, какие два пункта наиболее удалены друг от друга (при условии, что передвигаться можно только по указанным на схеме дорогам). В ответе укажите кратчайшее расстояние между этими пунктами.

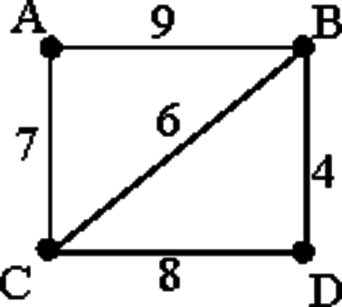
Заметим, что наиболее удалены друг от друга пункты A и D. Найдём все варианты маршрутов из A в D и выберем самый короткий. A—B—D: длина маршрута 13 км. A—C—D: длина маршрута 15 км. A—B—C—D: длина маршрута 23 км. A—C—B—D: длина маршрута 17 км. Заметим, что кратчайшее расстояние между пунктами A и D равняется 13. Ответ: 13

На рисунке — схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж и К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К?

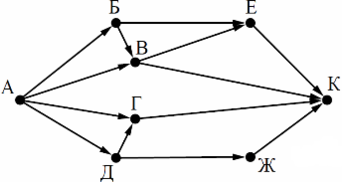
Начнем считать количество путей с конца маршрута — с города К. Пусть NX — количество различных путей из города А в город X, N — общее число путей. В К можно приехать из Е, В, Г или Ж, поэтому N = NК = NЕ + NВ + N Г + NЖ (*). Аналогично: NЕ = NБ + NВ = 1 + 2 = 3; NЖ = NД = 1; NВ = NА + NБ = 1 + 1 = 2; NГ = NА + NД = 1 + 1 = 2; NД = NА = 1; NБ = NА = 1. Подставим в формулу (*): N = 3 + 2 + 2 + 1 = 8. Ответ: 8
_____________________________________

Между населёнными пунктами A, B, C, D, E построены дороги, протяжённость которых (в километрах) приведена в таблице.

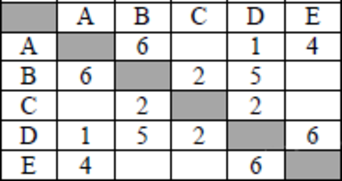
Определите длину кратчайшего пути между пунктами B и E. Передвигаться можно только по дорогам, протяжённость которых указана в таблице.

Проанализируем некоторые возможные маршруты. Маршрут B—D—E, длина 11 км. Маршрут B—C—D—E, длина 10 км. Маршрут B—С—D—A—E, длина 9 км. Любые другие маршруты будут длиннее маршрута B—С—D—A—E. Самый короткий путь: B—С—D—A—E. Длина маршрута 9 км. Ответ: 9