ОГПУ ДПО КУРСКИЙ ИНСТИТУТ РАЗВИТИЯ ОБРАЗОВАНИЯ
Рациональные уравнения
Рациональным уравнением называется равенство с одним или несколькими неизвестными, в правой и левой частях которого содержатся только рациональные выражения.
Очень важно уметь определять тип, поскольку от этого зависит правильность нахождения корней методика решения.
Рациональные уравнения бывают двух видов: целые и дробные.
Целые рациональные уравнения бывают линейными, квадратными, кубическими, биквадратными, а также уравнения высших степеней. Для каждого вида существуют определенные методики решения.
Рассмотрим более подробно возвратные уравнения.
Возвратными называют такие уравнения, в которых коэффициенты, одинаково удаленные от начала и конца, равны между собой.
Возвратные уравнения третьей степени – это уравнения вида
ax3 + bx2 + bx + a = 0, (1)
a ≠ 0, где а, b – заданные числа.
Поскольку ax3 + bx2 + bx + a = a( x3 + 1 ) + bx( x + 1) =
a( x + 1) ( x2 – x + 1 ) + bx( x + 1 ) = ( x + 1 ) ( ax2 + ( b – a )x + a ), то уравнение (1) равносильно совокупности уравнений
x + 1 = 0, ax2 + ( b – a ) = 0, решить которую не составит труда.
Пример 1. Решить уравнение 2х3 + 7х2 + 7х + 2 = 0.
2х3 + 7х2 + 7х + 2 = 0
( 2х3 + 2 ) + ( 7х2 + 7х ) = 0
2( х3 + 1 ) + 7х( х + 1 ) = 0
2( х + 1 )( х2 – х + 1 ) + 7х( х + 1) = 0
( х + 1 )( 2х2 + 5х + 2 ) = 0
х + 1 = 0 или 2х2 + 5х + 2 = 0
х = - 1 х1 = - 0,5; х2 = - 2
Ответ: -2; - 1; - 0,5.
Возвратное уравнение четвертой степени – это уравнение вида
ax4 + bx3 + cx2 + bx + a = 0, (2)
а также уравнения вида
ax4 + bx3 + cx2 - bx + a = 0, (3)
где a, b, c – заданные числа.
Так как а ≠ 0, то х = 0 не является корнем уравнения. Поэтому если разделить обе части уравнения (2) на х2, то в результате получится уравнение
ax2 + bx + c + 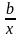 +
+ 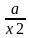 = 0.
= 0.
( ax2 + 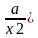 + ( bx +
+ ( bx + 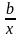 ) +c = 0.
) +c = 0.
a(x2 + 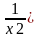 + b(x +
+ b(x + 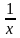 ) +c = 0. (4)
) +c = 0. (4)
Введем новую переменную у = x + 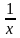 .
.
Так как у2 = ( х2 + 2 + 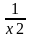 ), то x2 +
), то x2 + 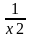 = у2 – 2.
= у2 – 2.
Получим а( у2 – 2) + by + c = 0.
Решив это уравнение, найдем его корни у1 и у2.
Чтобы найти х, остается решить совокупность уравнений
x + 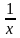 = у1, x +
= у1, x + 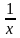 = у2. Она сводится к совокупности квадратных
= у2. Она сводится к совокупности квадратных
уравнений: х2 – у1х + 1 = 0, х2 – у2 + 1 = 0.
Уравнение (3) сводится к уравнению
a(x2 + 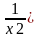 + b(x -
+ b(x - 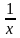 ) +c = 0.
) +c = 0.
После этого вводят замену у = x - 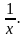 Так как у2 = х2 - 2 +
Так как у2 = х2 - 2 + 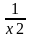 , то уравнение сводится к квадратному уравнению
, то уравнение сводится к квадратному уравнению
а( у2+2) + by + c = 0.
Дальнейшее решение ведется так же, как и для обычных возвратных уравнений.
Пример 2. Решить уравнение 6х4 – 35х3 + 62х2 – 35х + 6 = 0.
6х4 – 35х3 + 62х2 – 35х + 6 = 0 | ˸ х2≠0
6х2 – 35х + 62 - 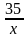 +
+  = 0
= 0
( 6х2 +  ) – (35х +
) – (35х + 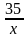 ) + 62 = 0
) + 62 = 0
6(x2 + 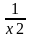 ) – 35(x +
) – 35(x + 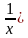 + 62 = 0
+ 62 = 0
Замена: x + 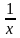 = у. у2 = (x +
= у. у2 = (x + 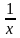 )2, x2 +
)2, x2 + 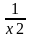 = у2 – 2.
= у2 – 2.
6( у2 – 2 ) – 35у + 62 = 0
6у2 – 35у + 50 = 0
у1 = 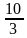 , у2 =
, у2 = .
.
Вернемся к замене:
x + 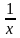 =
= x +
x + 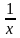 =
=  .
.
Решая квадратные уравнения 3х2 – 10х + 3 = 0 и 2х2 – 5х + 2 = 0, получаем корни: 3;  ;
;  ; 2.
; 2.
Ответ:  ;
;  ; 2; 3.
; 2; 3.
Пример 3. Решить уравнение 6х4 – 25х3 + 12х2 + 25х + 6 = 0.
6х4 – 25х3 + 12х2 + 25х + 6 = 0. | ˸ х2≠0
6х2 – 25х + 12 -  +
+  = 0
= 0
( 6х2 +  ) + (- 25х +
) + (- 25х +  ) + 12 = 0
) + 12 = 0
6(x2 + 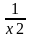 ) - 25(x -
) - 25(x - 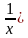 + 12 = 0
+ 12 = 0
Замена: x - 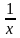 = у. у2 = (x -
= у. у2 = (x - 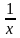 )2, x2 +
)2, x2 + 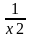 = у2 + 2.
= у2 + 2.
6( у2 + 2 ) – 25у + 12 = 0
6у2 – 25у + 24 = 0
у1 =  , у2 =
, у2 = .
.
Вернемся к замене:
x - 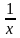 =
= x -
x - 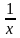 =
=  .
.
Решая квадратные уравнения 3х2 – 8х - 3 = 0 и 2х2 – 3х - 2 = 0, получаем корни: 3;  ;
;  ; 2.
; 2.
Ответ:  ;
;  ; 2; 3.
; 2; 3.
Схема Горнера при решении уравнений высших степеней.
Схема Горнера состоит в том, чтобы сначала найти какой-либо корень уравнения а0хп + а1хп-1 + а2хп-2 + … +ап-1х + ап = 0 через делители свободного члена.
После этого составляется специальная таблица с результатами деления на ( х – α ), в которой каждый член зависим от предыдущего. Коэффициенты из данной таблицы используются как коэффициенты в полученном от деления частного многочлене, они вычисляются по формулам:
b0 = a0; b1 = αb0 + a1; b2 = αb1 + a2; … bn-1 = αbn-2 + an-1; bn = αbn-1 + an.
|
| a0 | a1 | a2 | … | an |
| α | b0 = a0 | b1 = αb0 + a1 | b2 = αb1 + a2 | … | r = αbn-1 + an |
Пример 4. Решить уравнение х3 + 4х2 + х – 6 = 0.
х3 + 4х2 + х – 6 = 0
Выпишем делители свободного члена:  1;
1; 


Запишем коэффициенты в таблицу:
|
| 1 | 4 | 1 | -6 |
| 1 | 1 | 1·1+4=5 | 1·5+1=6 | 1·6+(-6)=0 |
Отсюда получаем, что многочлен, полученный от деления на ( х – α ) при α = 1, равен х2 + 5х + 6 = 0.
Исходное уравнение принимает вид:
( х – 1)( х2 + 5х + 6 ) = 0.
Корни многочлена х2 + 5х + 6 равны х2,3 = - 2; - 3.
Ответ: - 3; - 2; 1.
Пример 5. Решить уравнение х6 - 14х4 + 56х2 – 64 = 0.
Делители свободного члена: 
|
| 1 | 0 | - 14 | 0 | 56 | 0 | - 64 |
| 1 | 1 | 1 | - 13 | - 13 | 43 | 43 | - 21 |
| - 1 | 1 | - 1 | - 13 | 13 | 30 | - 30 | - 34 |
| 2 | 1 | 2 | - 10 | - 20 | 16 | 32 | 0 |
Так как х = 2 – корень, то данное уравнение запишем в виде
( х – 2 )( х5 + 2х4 -10х3 -20х2 + 16х + 32 ) = 0.
К многочлену 5-ой степени также применим схему Горнера.
|
| 1 | 2 | - 10 | - 20 | 16 | 32 |
| 1 | 1 | 3 | - 7 | - 27 | - 11 | 21 |
| - 2 | 1 | 0 | - 10 | 0 | 16 | 0 |
х = - 2 - корень
( х – 2 )( х + 2 )( х4 – 10х2 + 16 ) = 0
Корни уравнения х4 – 10х2 + 16 = 0:  (замена х2 = у ).
(замена х2 = у ).
Ответ: 
Пример 6. 2х4 – 5х3 + 5х2 – 2 = 0.
Воспользуемся схемой Горнера
|
| 2 | - 5 | 5 | 0 | - 2 |
| 1 | 2 | - 3 | 2 | 2 | 0 |
х =1 – корень
( х – 1)( 2х3 – 3х2 + 2х + 2 ) = 0
Будем искать корни среди делителей свободного члена 2.
|
| 2 | - 3 | 2 | 2 |
| 1 | 2 | - 1 | 1 | 3 |
| - 1 | 2 | - 5 | 7 | - 5 |
| 2 | 2 | 1 | 4 | 10 |
| - 2 | 2 | - 7 | 16 | - 30 |
Выяснили, что целых корней больше нет. Проверим ½, - ½.
|
| 2 | - 3 | 2 | 2 |
| 1/2 | 2 | - 2 | 1 | 2,5 |
| - 1/2 | 2 | - 4 | 4 | 0 |
х = - ½ - корень
Итак, ( х – 1 )( х + ½)( 2х2 – 4х + 4 ) = 0.
Далее решаем квадратное уравнение 2х2 – 4х + 4 = 0.
Это уравнение корней не имеет, так как дискриминант 
Ответ: 1; - ½.
Однородные уравнения.
Уравнения, имеющие структуру однородного, могут встретиться при решении показательных, логарифмических тригонометрических уравнений.
Однородные уравнения имеют такую структуру:
А□2 + В□·○ + С○2 = 0
В этом равенстве А, В, С – числа, а квадратиком и кружочком обозначены одинаковые выражения. То есть в левой части однородного уравнения стоит сумма одночленов, имеющих одинаковую степень ( в данном случае степень одночленов равна 2), и свободный член отсутствует.
Чтобы решить однородное уравнение, разделим обе части на ○2
или на □·○ или на □2.
При делении левой и правой части уравнения на выражение, содержащее неизвестное , можно потерять корни. Поэтому необходимо проверить, не являются ли корни того выражения, на которое мы делим обе части уравнения, корнями исходного уравнения.
Пойдем первым путем (разделим на выражение при А), сократим дроби, получим новое уравнение, которое будем решать с помощью замены, т.е.
Ау2 + Ву + С = 0.
Пример 7. Решить уравнение 2( х2 + х + 1 )2 – 7( х – 1 )2 = 13( х3 – 1 ).
2( х2 + х + 1 )2 – 7( х – 1 )2 - 13( х – 1 )( х2 + х + 1 ) = 0 – однородное уравнение.
Разделим обе части этого уравнения на ( х – 1 )2 , предварительно проверив, что х = 1 не является корнем исходного уравнения.
2  - 13
- 13 - 7 = 0
- 7 = 0
2( )2 – 13(
)2 – 13( -7 = 0.
-7 = 0.
Введем новую переменную: у  .
.
Получим квадратное уравнение 2у2 – 13у – 7 = 0.
Решив его, получим корни: 7; - ½.
Возвращаясь к замене, найдем корни исходного уравнения: 2; 4; - 1; - ½. Ответ: 2; 4; - 1; - ½.
Уравнения вида (х + а)4 + ( х + b )4 = c.
Это уравнение имеет структуру: □4 + ○4 = А и решается с помощью вот такой замены: t = 
Пример 8. Решить уравнение ( х + 3 )4 + ( х + 1 )4 = 272.
В нашем уравнении t =  = х + 2, тогда х = t – 2.
= х + 2, тогда х = t – 2.
Введем замену: ( t + 1 )4 + ( t – 1 )4 = 272.
Теперь возведем каждую скобку в четвертую степень, используя треугольник Паскаля:
t4 + 4t3 + 6t2 + 4t + 1 + t4 – 4t3 + 6t2 - 4t + 1 = 272
Упростим выражение и получим биквадратное уравнение относительно t:
2t4 + 12t2 – 270 = 0, t = - 3; 3.
Решив это уравнение и вернувшись к замене, получим корни исходного уравнения:  - 5; 1.
- 5; 1.
Ответ: - 5; 1.
Уравнения вида ( х + а ) ( х + b ) ( x + c ) ( x + d ) = Ax2.
Уравнение такого вида решается следующим образом:
Группируем скобки по две так, чтобы произведение свободных членов было одинаковым.
Перемножаем каждую пару скобок.
Из каждого множителя выносим за скобку х.
Делим обе части уравнения на х2.
Вводим замену переменной.
Пример 9. Решить уравнение ( х + 2 ) ( х + 3 ) ( x + 8 ) ( x + 12 ) = 4x2.
В этом уравнении сгруппируем первую скобку с четвертой, а вторую с третьей, так как 2·12 = 3·8.
[( х + 2 ) ( х + 12 )] [( х + 3 ) ( x + 8 )] = 4х2.
( х2 + 14х + 24 ) (х2 + 11х + 24 ) = 4х2.
Заметим, что в каждой скобке коэффициент при х2 и свободный член одинаковые.
х( х + 14 +  ) х(х + 11 +
) х(х + 11 +  = 4х2
= 4х2
х2( х + 14 +  ) (х + 11 +
) (х + 11 +  = 4х2
= 4х2
Так как х = 0 не является корнем исходного уравнения, разделим обе части уравнения на х2. Получим:
( х + 14 +  ) (х + 11 +
) (х + 11 +  = 4.
= 4.
Теперь можем ввести замену переменной: t = х +  + 11.
+ 11.
Получим уравнение: ( t + 3 )t = 4, корни которого равны: - 4; 1.
Далее вернемся к замене и найдем корни исходного уравнения:
- 4; - 6;  ;
;  .
.
Ответ: - 4; - 6;  ;
;  .
.
Уравнение вида ( х + a ) (x + b ) ( x + c ) ( x + d ) = A.
Заметим, что в левой части уравнения стоит произведение четырех скобок, а в правой – число.
Сгруппируем скобки по две так, чтобы сумма свободных членов была одинаковой.
Перемножим их.
Введем замену переменной.
Пример 10. Решить уравнение ( х - 1 ) ( x - 7 ) ( х - 4 ) ( x + 2 ) = 40
В нашем уравнении сгруппируем первую скобку с третьей, а вторую с четвертой, так как (-1) + (-4) = (-7) + 2:
[( х - 1 ) ( x - 4 )] [( х - 7 ) ( x + 2 )] = 40
( х2 – 5х + 4 ) ( х2 – 5х - 14 ) = 40
Введем замену: t = х2 – 5х .
Получаем уравнение ( t + 4 ) ( t – 14 ) = 40.
Решив это уравнение и вернувшись к замене, найдем корни исходного уравнения.
Ответ: 2; 3;  ;
;  .
.
Задания для самостоятельной работы
Решить уравнения:
( 5 - х )4 + ( х - 2 )4 = 17. Ответ: 3; 4.
( х - 3 ) ( х + 4 ) ( x + 6 ) ( x - 2 ) = 10x2. Ответ: -3 - 3; 4.
- 3; 4.
( х - 1 ) ( х + 1 ) ( x + 3 ) ( x + 5 ) = 105. Ответ: - 6; 2.
х4 – 10х3 + 35х2 – 50х + 24 = 0. Ответ: 1; 2; 3; 4.
5х4 – 3х3 - 4х2 – 3х + 5 = 0 . Ответ: 1.
2х3 + 7х2 + 7х +2 = 0. Ответ: - 2; - 1; - ½.
2х4 – 3х3 - х2 – 3х + 2 = 0. Ответ: ½; 2.
2х4 – 15х3 + 40х2 – 45х + 18 = 0. Ответ: 1; 1,5; 2; 3.
х7 + 2х6 – 5х5 – 13х4 – 13х3 – 5х2 + 2х + 1 = 0. Ответ: - 1; 

10)( х + 5 )4 – 13х2( х + 5 )2 + 36х4 = 0. Ответ: - 5/3; 5; - 5/4; 5/2.
Интернет – ресурсы:
nauka.club
confetti-matematika.ru
www.resolventa.ru
urok.1sept.ru
ege-ok.ru






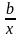 +
+ 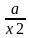 = 0.
= 0. 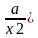 + ( bx +
+ ( bx + 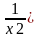 + b(x +
+ b(x + 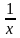 ) +c = 0. (4)
) +c = 0. (4)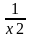 ), то x2 +
), то x2 + 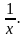 Так как у2 = х2 - 2 +
Так как у2 = х2 - 2 + 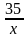 +
+  = 0
= 0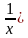 + 62 = 0
+ 62 = 0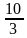 , у2 =
, у2 =









