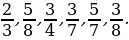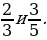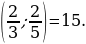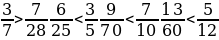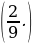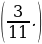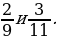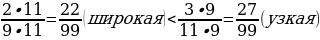Разработка урока № 1 "Сравнение, сложение и вычитание дробей с разными знаменателями" (5 класс, учебник Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков и др.)

У р о к № 1. Сравнение, сложение и вычитание

дробей с разными знаменателями

Основная дидактическая цель урока: поставить проблему по теме урока и найти пути её решения, вывести правила сравнения дробей с разными знаменателями, учить сравнивать дроби с разными знаменателями, продолжить формирование коммуникативных отношений.

Х о д у р о к а

I. Организационный момент

II. Устная работа

– Давайте вспомним, как сравнивают дроби с одинаковыми знаменателями или с одинаковыми числителями.

– Какое правило сравнения дробей вы использовали?

(Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.)

– Как сравнивать дроби с одинаковыми числителями?

(Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше.)

1. Сравните дроби, выполните сложение и вычитание дробей с одинаковыми знаменателями:

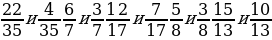
2. Определите, какая из дробей наибольшая, какая – наименьшая.

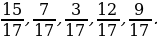
– Расположите данные дроби в порядке возрастания.

– Почему вы расположили дроби именно так?

3. Расположите дроби в порядке убывания.

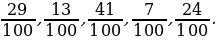
4. Блиц-опрос.

• Сформулируйте основное свойство дроби.

• Какую дробь называют несократимой?

• Какие числа называются взаимно простыми?

• Как сравнить, сложить, вычесть дроби с разными знаменателями?

• Каким может быть общий знаменатель дробей ?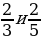

III. Работа по теме урока

– Какие дроби мы с вами ещё не сравнивали? (Дроби с разными знаменателями и разными числителями.)

1. Рассмотрите дроби.

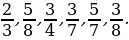
– Что вы заметили? (Знаменатели и числители у дробей разные.)

– Найдите среди этих дробей самую маленькую и самую большую.

У нас возникла проблема: как сравнить дроби с разными знаменателями. Чтобы ответить на вопрос, мы проведём исследовательскую работу. Работать будем в группах по инструкции.

(Инструкция записана на доске.)

Инструкция

1) Внимательно рассмотрите числа.

2) Расположите дроби на координатном луче, самостоятельно выберите единичный отрезок.

3) Сравните полученные отрезки. Сделайте вывод.

4) Расположите дроби в порядке возрастания. Выделите наименьшую дробь зелёным цветом, а наибольшую – красным.

5) Постарайтесь сформулировать вывод: как сравнить дроби с разными знаменателями.

– Скажите, удобно ли каждый раз, сравнивая дроби, отмечать их на координатном луче?

– Как же сравнивать такие дроби?

– Сформулируйте правило сравнения дробей с разными знаменателями и числителями.

2. Сравните дроби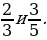

– Приведём дроби к наименьшему общему знаменателю.

(Так как 3 и 5 – взаимно простые числа, то НОЗ дробей будет их произведение.)

НОЗ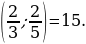

IV. Работа по учебнику

1. С. 66, № 5.393.

– Как сравнивать дроби с разными знаменателями? (Надо привести дроби к наименьшему общему знаменателю.)

– Как сравнивать дроби с одинаковыми знаменателями?

(Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.)

– Приведём дроби к наименьшему общему знаменателю. (28, 25, 70, 60.)

Ответ:

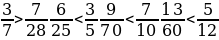
2. С. 66, № 5.394.

3. С. 66, № 5.396.

4. С. 67, № 5.403.

5. С. 67, № 5.404 (работа в паре).

V. Работа над задачей

1. С. 67, № 5.403.

– Что нужно сделать, чтобы ответить на вопрос задачи? (Сравнить дроби.)

– Как нужно сравнивать дроби с одинаковыми знаменателями?

– Как нужно сравнивать дроби с разными знаменателями?

2. С. 67, № 5.405.

– Что известно в задаче? Что надо узнать?

– За сколько часов широкая труба наполняет весь бассейн? (За 9 ч.)

– Какую часть бассейна заполнит широкая труба за 2 ч?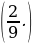

– За сколько часов узкая труба наполняет весь бассейн? (За 11 ч.)

– Какую часть бассейна заполнит узкая труба за 3 ч?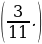

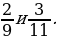
– Сравним дроби. Какой у них наименьший общий знаменатель? (99.)

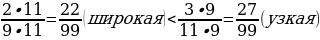
Ответ: узкая труба за 3 ч подаёт в бассейн больше воды.

VI. Рефлексия

– Как сравнивать дроби с одинаковыми знаменателями?

– Как сравнивать дроби с одинаковыми числителями?

– Как сравнивать дроби с разными знаменателями?

Домашнее задание

С. 71, № 5.444, 5.447; c. 72, № 5.448.
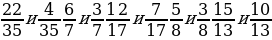
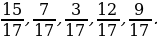
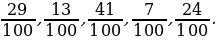
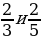