Разработка урока на тему "Решение нестандартных задач"

1.

Организационный момент. (2 мин)

Проверить количество учащихся, готовность к уроку

2.

Проверка и разбор домашнего задания.

3.

Ход урока:

1.Сообщение темы и целей урока.

2. Исторические сведения. Слово "математика возникло примерно в V веке до н.э. Происходит оно от слова "матема"- "учение", "знание, полученные через размышление"

Древние греки знали четыре "матемы":

1. Теория музыки.

2. Учение о числах.

3. Учение о числах и измерениях.

4. Астрономию и астрологию.

В древнегреческой науке существовало два направления. Представители первого из них, возглавляемые Пифагором, считали, что знания принадлежат только посвящённым, избранным. Никто не имел права делиться своими открытиями и знаниями с посторонними.

Второе направление возглавлял Гиппас Метапонтский. Его последователи, напротив, считали, что математика доступна всем, кто способен к продуктивным размышлениям. Они называли себя математиками. Как вы думаете, какое направление победило?

Пифагор - довольно известный персонаж, но он меньше всего хотел, чтобы знания были доступны всем, а Гиппас - почти неизвестная личность проложил дорогу наукам.

Древние говорили, что умение решать необычные задачи - умение крайне нужное и полезное.

Просмотр слайдов «Открытия юных математиков»

3. Устный счет.

Сегодня мы научимся быстро умножать на 11. Умножать на 11 чуть сложнее, чем умножать на 10. Закономерность здесь такая:

53 х 11 = 583
Шаг 1 — Складываем две цифры двузначного числа: 5 + 3 = 8
Шаг 2 — Помещаем результат между двумя числами двузначного числа: 583

59 х 11 = 649
Шаг 1 — 5 + 9 = 14
Шаг 2 — Перекидываем единицу налево, если сумма на предыдущем шаге оказалась больше 9: 5 + 1 = 6 (справа остается второй символ, в данном случае это четверка)
Шаг 3 — На первый символ мы единицу уже перекинули, получили 6. Далее у нас осталась 4, которую ставим в центр, и дописываем 9: 649

Вычислите устно: 63 х 11, 27 х11, 37х11

4.

Работа по теме урока:

1.Задачи, решаемые с конца.

Если в задаче задана некоторая операция, и эта операция обратима, то можно сделать «обратный ход» от конечного результата к исходным данным

Задача 1. Однажды черт предложил бездельнику заработать. “Как только ты перейдешь через этот мост, – сказал он, – твои деньги удвоятся. Можешь переходить по нему сколько хочешь раз, но после каждого перехода отдавай мне за это 24 рубля”. Бездельник согласился и … после третьего перехода остался без денег. Сколько денег у него было сначала?

Решение. Начнем с конца. Так как после третьего перехода у бездельника денег не осталось, то после перехода моста в третий раз у него было 24 руб., а до перехода третьего моста – 12 руб.

Тогда после перехода второго моста у бездельника было

12 + 24 = 36 (руб.),

а до перехода второго моста – 36 : 2 = 18 (руб.).

Рассуждая аналогично, получим, что после перехода первого моста у бездельника стало 18 + 24 = 42 (руб.), а перед переходом первого моста – 42 : 2 = 21 (руб.).

Ответ: 21 рубль

2. Задачи на взвешивание и переливание

а)На одной чаше весов лежат 12 одинаковых лимонов и 6 одинаковых апельсинов. На другой – 6 таких же лимонов и 10 таких апельсинов. Весы находятся в равновесии. Что легче – лимон или апельсин?

в)В мешке 24 кг гвоздей. Как, имея только чашечные весы без гирь, отмерить 9 кг гвоздей?

Решение:

СОСТАВИМ ТАБЛИЦУ:

г) Когда за доброе дело правитель страны решил наградить умного человека, тот пожелал взять столько золота, сколько весит слон. Но как же взвесить слона? В те времена не было таких весов. Что бы в подобной ситуации придумали вы?

Ответ: 

Мудрец сделал так: он поместил слона в лодку, затем отметил по борту уровень воды. Когда слона вывели из лодки, осталось только поместить туда золото.

д) Как, имея пятилитровую банку и девятилитровое ведро, набрать из реки ровно три литра воды? 

Решение:

Составим таблицу:

Ш.Задачи на теорию множеств(решается с помощью кругов Эйлера).

Из 52 школьников 23 собирают значки,35 собирают марки , а 16 и значки и марки . Остальные не увлекаются коллекционированием . Сколько школьников не увлекается коллекционированием?

Решение: Для решения используем круги Эйлера.

1)23-16=7(чел.) собирают только значки;
2)35-16=19(чел.) собирают только марки;
3)7+19+16=42 (чел.) занимаются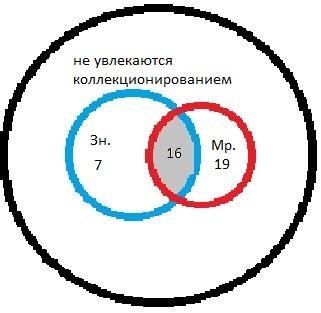

коллекционированием;
4)52-42=10(чел.) не увлекается

коллекционированием.

ОТВЕТ: 10 человек

5.

Работа в парах:

Самостоятельная работа по карточкам:

1. Я задумала число, прибавила к нему 5, потом разделила сумму на 3, умножила на 4, отняла 6, разделила на 7 и получила число 2. Какое число я задумала?

2. Имеются стандартные весы с чашечками и гиря, весом 2 кг. Как с их помощью взвесить 3 кг слив?

3.На полке стояло 26 волшебных книг по заклинаниям, все они были прочитаны. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал только Рон?

Проверка ответов по слайдам

6.

Оценивание. Подведение итогов

Выставление оценок за самостоятельную работу.

Учитель предлагает ребятам составить кластер из понятий, связанных с темой урока «Нестандартные задачи»

7.

Домашнее задание

1. Нужно рассадить 22 туристов в двухместные и четырехместные лодки. Сколько тех и других лодок потребуется, если всего лодок 8?

2. Винни-Пух разлил 60 л меда в 9 горшочков двух видов — вместимостью 4 и 8 л. Сколько горшков каждого вида занял Винни-Пух?

Домашнее задание

1. Нужно рассадить 22 туристов в двухместные и четырехместные лодки. Сколько тех и других лодок потребуется, если всего лодок 8?

2. Винни-Пух разлил 60 л меда в 9 горшочков двух видов — вместимостью 4 и 8 л. Сколько горшков каждого вида занял

Винни-Пух?