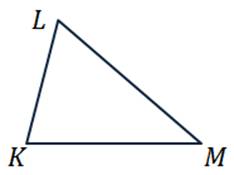Геометрия, 9 класс
Урок №1
Тема: ПОНЯТИЕ ВЕКТОРА. РАВЕНСТВО ВЕКТОРОВ
РЕБЯТА! СЕГОДНЯ МЫ НАЧИНАЕМ ИЗУЧАТЬ НОВЫЙ МЕТЕРИАЛ!
Из физики вам известно, что некоторые величины полностью характеризуются числовым значением (площадь, объем, температура). Их называют скалярными величинами или скалярами.
Но есть и такие величины, которые характеризуются не только своим численным значением, но и направлением: сила, скорость, перемещение. Например, мало знать, что скорость поезда равна 50 км/ ч.
Надо знать еще в каком направлении движется этот поезд. Указать направление можно, например, стрелкой.
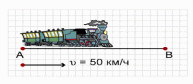
Так, поезд движется со скоростью 50 км/ч из пункта А в пункт В. Величины, которые характеризуются не только своими числовыми значениями, но направлением, называются векторными величинами или векторами.
Перейдём к геометрическому понятию вектора.
Рассмотрим отрезок произвольной величины АВ. Его концы – точки А и В – граничные точки отрезка.

На данном отрезке можно указать два направления: от точки B к точке А и наоборот.
Чтобы выбрать одно из направлений, одну граничную точку назовем началом, а другую — концом. Теперь будем считать, что отрезок направлен от начала к концу.

Отрезок, для которого указано, какая из его граничных точек считается началом, а какая — концом, называется направленным отрезком или вектором.
ОПРЕДЕЛЕНИЕ
Отрезок, для которого обозначены начало и конец, называется направленным отрезком или вектором.
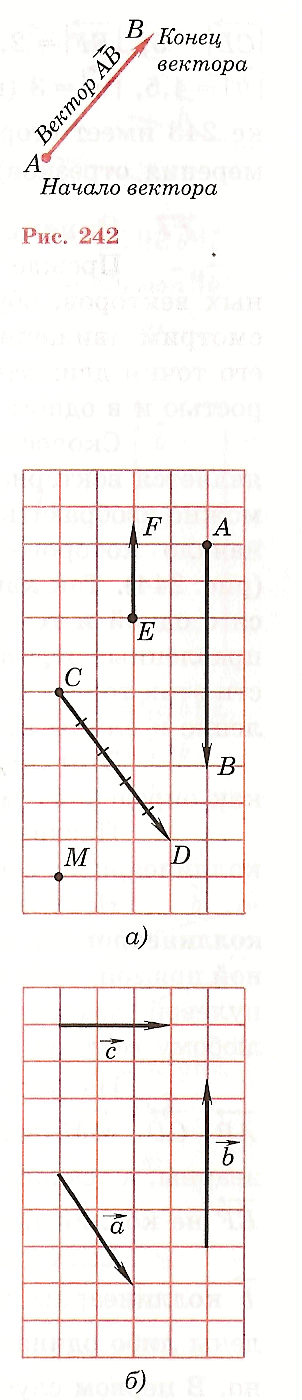
Обозначение вектора – двумя заглавными латинскими буквами со стрелкой над ними, например 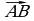 , где А – начало вектора, В – конец вектора или часто вектор обозначают одной строчной латинской буквой со стрелкой над ней:
, где А – начало вектора, В – конец вектора или часто вектор обозначают одной строчной латинской буквой со стрелкой над ней: 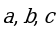 .
.
| 
|
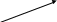 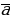 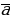 , , 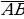 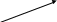 А – начало вектора В В – конец вектора А
|
Вектор – это направленный отрезок.
Первая буква обозначает начало вектора, а вторая — конец.
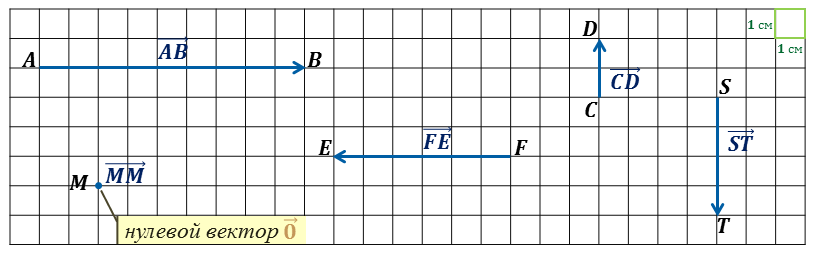
Задание №1. Назовите векторы, изображенные на рисунке №1.
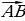 ,
, 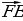 ,
, 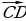 ,
, 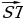 ,
, 
Задание №2. Отметьте три точки А, В и С, не лежащие на одной прямой. Начертите векторы 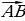 ,
, 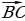 ,
, 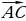 .
.
Понятие нулевого вектора: любая точка плоскости также является вектором; в этом случае вектор называется нулевым; обозначают такой вектор двумя одинаковыми заглавными латинскими буквами 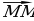 - или
- или 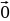 .
.
Длиной или модулем ненулевого вектора 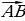 называется длина отрезка АВ. Длина вектора
называется длина отрезка АВ. Длина вектора 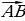 (вектора
(вектора 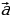 ) обозначается так:
) обозначается так: 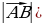
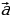 ).
).
Длина нулевого вектора считается равной нулю: 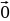 =0.
=0.
Задание №3. Допустим, что каждая клетка на рисунке в задании №1 имеет сторону длиной в 1 сантиметр. Определим длину каждого вектора:
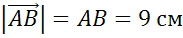
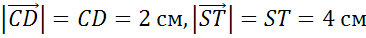 ,
,
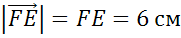
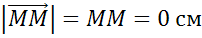 .
.
Теперь перейдем к изучению равных векторов.
Для этого введём понятие коллинеарных векторов.
Коллинеарные векторы – это ненулевые векторы, если они лежат либо на одной прямой либо на параллельных прямых.
Нулевой вектор считается коллинеарным любому вектору.
Посмотрим на рисунок №2 и найдём на нём коллинеарные векторы.
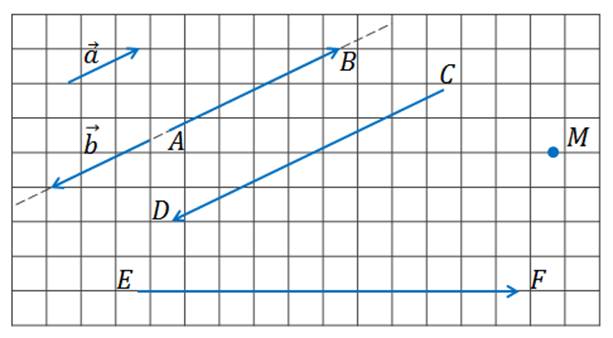
Векторы 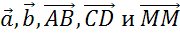 коллинеарны.
коллинеарны.
Также коллинеарны будут векторы 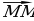 и
и 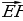 , ведь нулевой вектор
, ведь нулевой вектор 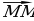 коллинеарен любому вектору.
коллинеарен любому вектору.
А вот, например, векторы 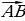 и
и 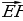 ,
, 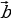 и
и 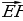 не коллинеарны.
не коллинеарны.
Рассмотрим два коллинеарных вектора 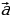 и
и 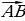 . Они одинаково направлены. А вот коллинеарные векторы
. Они одинаково направлены. А вот коллинеарные векторы 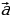 и
и 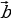 противоположно направлены.
противоположно направлены.
Сонаправленные векторы (коллинеарные векторы, направленные в одну сторону). Обозначение: 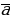
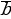 .
.
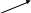

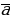
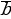
Противоположно направленные (коллинеарные векторы, направленные в противоположные стороны)
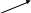
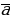 Обозначение:
Обозначение: 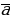
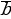 .
.
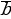
Т.к. у нулевого вектора начало и конец совпадают, поэтому определенного направления он не имеет.
Определение.
Векторы называются равными, если они сонаправлены и их длины равны.
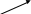
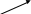
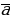
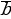 Если
Если 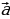
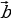 и
и 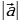
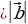 , то векторы
, то векторы 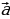 =
= 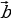
Любые два нулевых вектора равны.
Если точка А является началом вектора А, то говорят что вектор А отложен от точки А.
Имеет место следующее утверждение.
От любой точки можно отложить вектор, равный данному вектору, и притом только один.
Перейдем к решению задач.
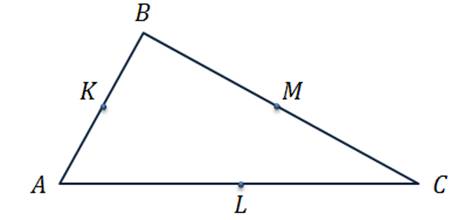
Задача №1. В треугольнике АВС стороны АВ , ВС и АС равны 4см, 7 см и 10 см. Точки К, М, L — середины сторон AB? BC? AC треугольника.
Найти длины векторов 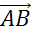 ,
, 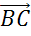 ,
, 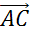 ,
, 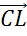 ,
, 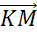 ,
, 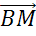 и
и 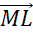 .
.
Решение
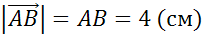
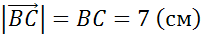
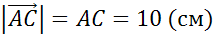
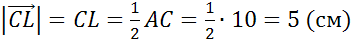
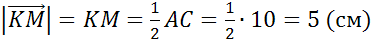
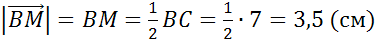
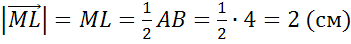
Задача №2. Стороны прямоугольника ABCD равны 6 см и 8 см. Найти длину вектора 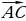 .
.
Решение
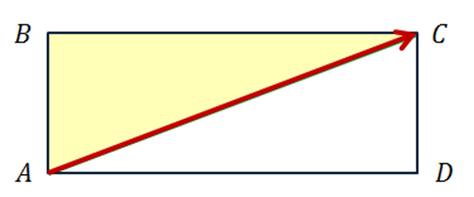
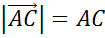
Рассмотрим 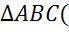 прямоугольный
прямоугольный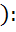
по теореме Пифагора 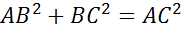
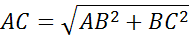
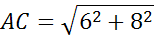
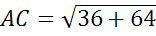
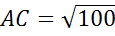

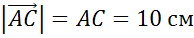
Ответ: 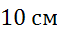 .
.
Задача №3. Начертить векторы 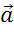 ,
, 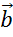 и
и 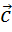 так, чтобы
так, чтобы 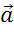 и
и 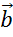 были коллинеарны, а векторы
были коллинеарны, а векторы 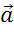 и
и 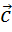 были не коллинеарны и длины векторов
были не коллинеарны и длины векторов 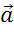 ,
, 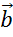 и
и 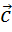 были соответственно равны
были соответственно равны 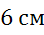 ,
, 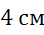 и
и 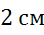 .
.
Решение

Чтобы векторы 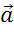 и
и 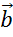 были коллинеарны, они должны лежать, например, на параллельных прямых. Причём длина вектора
были коллинеарны, они должны лежать, например, на параллельных прямых. Причём длина вектора 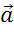 равна 6 см, а длина вектора
равна 6 см, а длина вектора 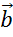 — четырём см.
— четырём см.
Вектор 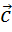 изобразим так, чтобы он был не коллинеарным с вектором
изобразим так, чтобы он был не коллинеарным с вектором 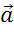 , а длина его была равна 2 см.
, а длина его была равна 2 см.
Перейдём к следующей задаче.
Задача №4. Выписать пары коллинеарных векторов, которые определяются сторонами:
а) квадрата АВСD;
б) треугольника KLM;
в) трапеции RSTV, где ST и RV — основания трапеции.
Решение
а) Изобразим квадрат ABCD. Коллинеарные векторы лежат на одной прямой или на параллельных прямых.
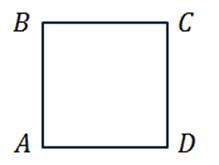
Рассмотрим параллельные стороны BC и АD. Можем записать такие пары коллинеарных векторов: 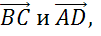
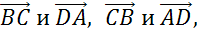
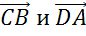
Рассмотрим параллельные стороны AB и CD. Можно записать следующие пары коллинеарных векторов: 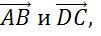
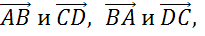
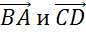 .
.
Также коллинеарными будут векторы 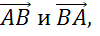
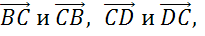
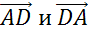 , так как они лежат на одной прямой.
, так как они лежат на одной прямой.
Получили 12 пар коллинеарных векторов.
б) изобразим треугольник KLM.
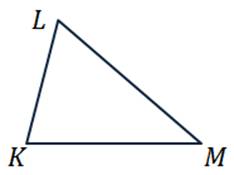
Никакие из его сторон не параллельны. Но коллинеарными будут векторы, лежащие на одной стороне: 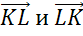 ,
, 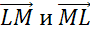 ,
, 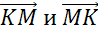 .
.
Получили 3 пары коллинеарных векторов.
в) изобразим трапецию PSTV так, чтобы стороны ST и PV являлись её основаниями.
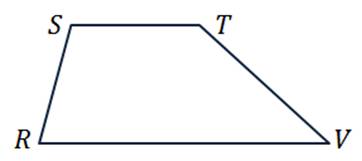
Параллельных сторон видим только две, поэтому запишем следующие пары коллинеарных векторов: 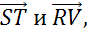
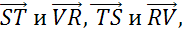
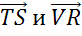 .
.
Также коллинеарными будут векторы, лежащие на одной стороне: 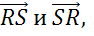
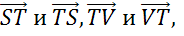
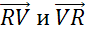 .
.
Получили 8 пар коллинеарных векторов.
Рассмотрим следующую задачу.
Задача №5. Диагонали параллелограмма 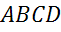 пересекаются в точке
пересекаются в точке 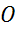 . Равны ли векторы:
. Равны ли векторы: 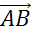 и
и 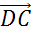 ,
, 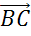 и
и 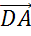 ,
, 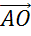 и
и 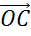 ,
, 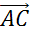 и
и 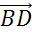 ?
?
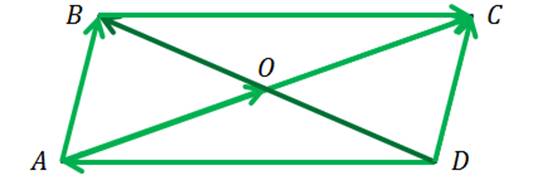
Решение

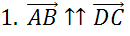 ,
, 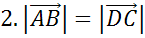
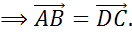
Следующая пара векторов 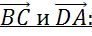
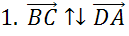 ,
, 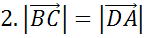
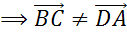 .
.
Далее обратим внимание на пару векторов 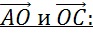
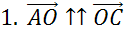 ,
, 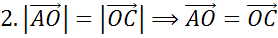 .
.
Последней рассмотрим пару векторов 
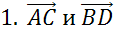 , не коллинеарны
, не коллинеарны 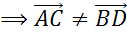 .
.
Задача № 750, учебник стр. 194: Доказательство
| 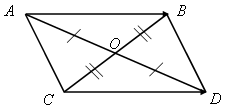
| По условию 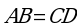 , то AB || CD, значит, по признаку параллелограмма АВDС – параллелограмм, а диагонали параллелограмма точкой пересечения делятся пополам, значит, середины отрезков AD и BC совпадают. , то AB || CD, значит, по признаку параллелограмма АВDС – параллелограмм, а диагонали параллелограмма точкой пересечения делятся пополам, значит, середины отрезков AD и BC совпадают. |
Домашнее задание.
Повторить основные понятия из конспекта.
Изучить п.79-81 (стр. 189-193) учебника, решить № 740 (а), № 746, №748
Посмотрите видео по теме урока https://www.youtube.com/watch?v=66jnOBZKRDQ
https://www.youtube.com/watch?v=RA9gLMQSME8










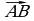 , где А – начало вектора, В – конец вектора или часто вектор обозначают одной строчной латинской буквой со стрелкой над ней:
, где А – начало вектора, В – конец вектора или часто вектор обозначают одной строчной латинской буквой со стрелкой над ней: 
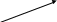
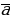
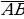

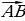 ,
, 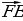 ,
, 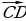 ,
, 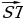 ,
, 
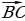 ,
, 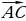 .
.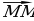 - или
- или 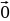 .
.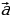 ) обозначается так:
) обозначается так: 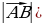

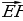 , ведь нулевой вектор
, ведь нулевой вектор 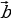 и
и 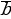 .
.

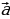
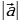
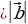 , то векторы
, то векторы