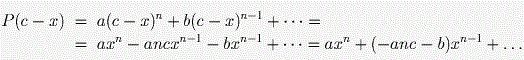Основные методы решения задач
метод рассуждений;
с помощью таблиц истинности;
метод блок-схем;
средствами алгебры логики (алгебры высказываний);
графический (в том числе, «дерево логических условий», метод кругов Эйлера);
метод математического бильярда.
Давайте рассмотрим подробнее с примерами три популярных способа решения логических задач, которые мы рекомендуем использовать в начальной школе (детям 6-12 лет):
метод последовательных рассуждений;
разновидность метода рассуждений — «с конца»;
табличный способ.
Метод последовательных рассуждений
Самый простой способ решения несложных задач заключается в последовательных рассуждениях с использованием всех известных условий. Выводы из утверждений, являющихся условиями задачи, постепенно приводят к ответу на поставленный вопрос.
Пример:
На столе лежат Голубой, Зеленый, Коричневый и Оранжевый карандаши.
Третьим лежит карандаш, в имени которого больше всего букв. Голубойкарандаш лежит между Коричневым и Оранжевым.
Разложи карандаши в описанном порядке.

Решение:
Рассуждаем. Последовательно используем условия задачи для формулирования выводов о позиции, на которой должен лежать каждый следующий карандаш.
Больше всего букв в слове «коричневый», значит, он лежит третьим.
Известно, что голубой карандаш лежит между коричневым и оранжевым. Справа от коричневого есть только одна позиция, значит, расположить голубой между коричневым и другим карандашом возможно только слева от коричневого.
Следующий вывод на основе предыдущего: голубой карандаш лежит на второй позиции, а оранжевый — на первой.
Для зеленого карандаша осталась последняя позиция — он лежит четвертым.
Метод «с конца»
Такой способ решения является разновидностью метода рассуждений и отлично подходит для задач, в которых нам известен результат совершения определенных действий, а вопрос состоит в восстановлении первоначальной картины.
Пример:
Бабушка испекла для троих внуков рогалики и оставила их на столе. Коля забежал перекусить первым. Сосчитал все рогалики, взял свою долю и убежал.
Аня зашла в дом позже. Она не знала, что Коля уже взял рогалики, сосчитала их и, разделив на троих, взяла свою долю.
Третьим пришел Гена, который тоже разделил остаток выпечки на троих и взял свою долю.
На столе осталось 8 рогаликов.
Сколько рогаликов из восьми оставшихся должен съесть каждый, чтобы в результате все съели поровну?
Решение:
Начинаем рассуждение «с конца».
Гена оставил для Ани и Коли 8 рогаликов (каждому по 4). Получается, и сам он съел 4 рогалика: 8 + 4 = 12.
Аня оставила для братьев 12 рогаликов (каждому по 6). Значит, и сама она съела 6 штук: 12 + 6 = 18.
Коля оставил ребятам 18 рогаликов. Значит, сам съел 9: 18 + 9 = 27.
Бабушка положила на стол 27 рогаликов, рассчитывая, что каждому достанется по 9 штук. Поскольку Коля уже съел свою долю, Аня должна съесть 3, а Гена — 5 рогаликов.
Решение логических задач с помощью таблиц истинности
Суть метода состоит в фиксации условий задачи и полученных результатов рассуждений в специально составленных под задачу таблицах. В зависимости от того, является высказывание истинным или ложным, соответствующие ячейки таблицы заполняются знаками «+» и «-» либо «1» и «0».
Пример:
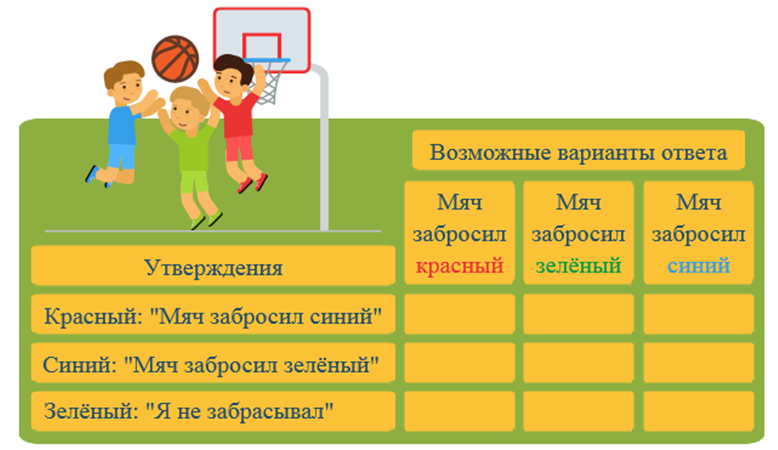
Три спортсмена (красный, синий и зеленый) играли в баскетбол.
Когда мяч оказался в корзине, красный воскликнул: «Мяч забросил синий».
Синий возразил: «Мяч забросил зеленый».
Зеленый сказал: «Я не забрасывал».
Кто забросил мяч, если только один из троих сказал неправду?
Решение:
Сначала таблицу составляют: слева записывают все утверждения, которые содержатся в условии, а сверху — возможные варианты ответа.
Затем таблицу последовательно заполняют: верные утверждения отмечают знаком «+», а ложные утверждения — знаком «-«.
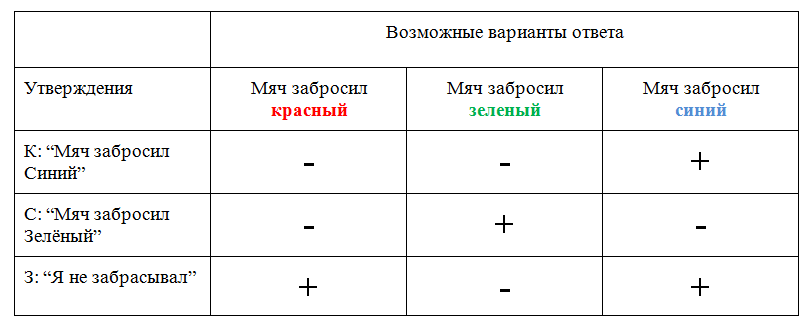
Рассмотрим первый вариант ответа («мяч забросил красный«), проанализируем утверждения, записанные слева, и заполним первый столбик.
Исходя из нашего предположения («мяч забросил красный«), утверждение «мяч забросил синий» — ложь. Ставим в ячейке «-«.
Утверждение «мяч забросил зеленый» также ложь. Заполняем ячейку знаком «-«.
Утверждение зеленого «Я не забрасывал» – истина. Ставим в ячейке «+».
Рассмотрим второй вариант ответа (предположим, что мяч забросил зеленый) и заполним второй столбик.
Утверждение «мяч забросил Синий» — ложь. Ставим в ячейке «-«.
Утверждение «мяч забросил зеленый« — истина. Заполняем ячейку знаком «+».
Утверждение зеленого «Я не забрасывал» – ложь. Ставим в ячейке «-«.
И, наконец, третий вариант: предположим, что «мяч забросил синий«.
Тогда утверждение «мяч забросил синий« — истина. Ставим в ячейке «+».
Утверждение «мяч забросил зеленый» — ложь. Заполняем ячейку знаком «-«. Утверждение зеленого «Я не забрасывал» – истина. Ставим в ячейке «+».
Так как по условию лишь один из троих ребят сказал неправду, в заполненной таблице выбираем такой вариант ответа, где будет только одно ложное утверждение (в столбце один знак «-«). Подходит третий столбец.
Значит, правильный ответ – мяч забросил синий.
Метод блок-схем
Метод блок-схем считается оптимальным вариантом для решения задач на взвешивание и на переливание жидкостей. Альтернативный способ решения этого типа задач — метод перебора вариантов — не всегда является оптимальным, да и назвать его системным довольно сложно.
Порядок решения задач по методу блок-схем выглядит следующим образом:
графически (блок-схемой) описываем последовательность выполнения операций;
определяем порядок их выполнения;
в таблице фиксируем текущие состояния.
Подробнее об этом и других способах решения логических задач с примерами и описанием хода решения мы рассказываем в полном Курсе ЛогикЛайк по развитию логического мышления.
Логические задачи.
1. Ствол у дуба толще, чем ствол у сосны, а ствол у сосны толще, чем ствол у березы. Что толще: ствол дуба или ствол березы? Ствол дуба.
2. Оля выше Веры, а Вера выше Наташи. Кто выше: Наташа или Оля? Оля
3. Дима старше Вани, а Ваня старше Марины. Кто старше: Дима или Марина? Дима
4. Ира родная сестра Киры. Витя – брат Иры. Пётр Сергеевич–дедушка Киры. Папу Иры зовут Виталием. Напиши имя и отчество папы Киры и отчество брата Иры. Папа-Виталий Петрович, брат-Виталий Витальевич.
5. Из трёх братьев Миша был выше Вити, а Витя выше Димы. Кто выше: Митя или Дима? Миша
6. Слева от квадрата находится треугольник, а справа от квадрата – круг. Где находится квадрат? Сделай рисунок. Треугольник, квадрат, круг
7. Девочки Катя, Галя и Оля спрятали медвежонка, зайчика и слоника. Катя не прятала зайчика, Оля не прятала ни зайчика, ни медвежонка. Кто какую игрушку спрятал? Оля - слоника, Катя - медведя, Галя - зайчика.
8. Три друга – Витя, Серёжа, Коля – раскрашивали рисунки карандашами трёх цветов: красным , синим, зелёным. Витя раскрашивал не красным и не синим карандашом, Коля – не синим. Каким карандашом пользовался каждый из мальчиков? Витя - зелёным, Серёжа – синим, Коля – красным.
9. Среди трёх футбольных мячей красный мяч тяжелее коричневого, а коричневый - тяжелее зелёного. Какой мяч самый тяжёлый? Красный
10. Игорь грустнее Жени. Женя грустнее Вовы. Кто грустнее всех? Игорь
11. Кто выше всех, если Ира и Лена одинакового роста, Лена выше Оля, а Таня выше Иры. Таня
12. На кормушке сидело 5 воробьёв и 2 синицы. Улетели 3 птицы. Был ли среди них хотя бы 1 воробей?
13. В пакете и в вазе было 10 груш. Из пакета все груши переложили в вазу. Сколько груш стало в вазе?
14. В детской площадке играли 6 девочек с косичками, 3 девочки в белых кофточках, а всего девочек было 7. Как же это может быть?
15. В велогонках участвовали медвежата – Тимка, Дружок и Огонёк. У финиша Тимка оказался не последним, а Огонёк пришел к финишу раньше Тимки. В каком порядке медвежата закончили велогонку?Огонёк 1, Тимка 2, Дружок 3
16. В цирковом представлении принимали участие медведь, тигр и обезьяна. В каком порядке они выходили на арену, если тигр был не последним, а медведь выступал раньше, чем тигр? Медведь, тигр, обезьяна.
17. В три чашки желтого, зеленого и синего цвета налили чай, молоко и сок. Какой напиток в каждой чашке, если чай не в синей и не в жёлтой чашке, а сок – не в синей? Чай в зеленой, сок в желтой, молоко в синей.
18. Наташа, Оля и Лена писали контрольную работу. Оля сдала работу не последней, а Наташа – раньше Оли. В каком порядке сдали работу?Наташа, Оля, Лена.
19. Три подруги – Мотя, Вера и Зоя – пошли в кино в платьях разного цвета: красном, голубом, синем. Мотя была не в красном и не в голубом, Зоя была не в голубом. В каком платье была каждая девочка? Мотя в синем, Зоя в красном, Вера в голубом.
20. Таня слепила из пластилина столько же игрушек, сколько и Наташа Таня начала лепить раньше Наташи, закончили девочки одновременно. Кто лепил быстрее? Наташа
21. Машина проехала из одного населенного пункта до другого столько километров, сколько минут она ехала. Какова скорость этой машины?
22. Алла, Катя и Люда получили оценку за работу по математике. Какую оценку получила каждая девочка, если “2” в классе нет, а у девочек отметки разные, причем у Аллы – не “3”, у Люды – не “3” и не “5”. У Люды “4”, у Аллы “5”, у Кати “3”.
23. Сколько будет, полсотни разделить на половину? 25.
| Математические задачи 11 класс с решением и ответами. Задача 1. О функции f(x), заданной на всей вещественной прямой,
известно, что при любом a 1 функция f(x) + f(ax) непрерывна на всей прямой.
Докажите, что f(x) также непрерывна на всей прямой.
Решение:
Мы воспользуемся следующими свойствами непрерывных функций: (1) сумма и разность непрерывных функций — непрерывные функции; (2) если g(x) — непрерывная функция, функция g(ax) также непрерывна.
Теперь заметим, что по условию непрерывны функции f(x) + f(2x) и f(x) + f(4x), а в силу свойства (2) вместе с функцией f(x) + f(2x) непрерывна и функция f(2x) + f(4x).
Далее, по свойству (1) непрерывна функция (f(x) + f(2x)) + (f(x) + f(4x)) – (f(2x) + f(4x)) = 2f(x), а, значит, и функция f(x).

Задача 2. В классе каждый ученик — либо болтун, либо молчун,
причем каждый болтун дружит хотя бы с одним молчуном.
Болтун молчит, если в кабинете находится нечётное число его друзей — молчунов.
Докажите, что учитель может пригласить на факультатив не менее половины класса так,
чтобы все присутствующие на факультативе болтуны молчали.
Решение:
Докажем утверждение индукцией по числу n учеников в классе.
Для n = 3 утверждение очевидно.
Предположим, что оно верно при n ≤ N. Пусть n = N + 1.
Утверждение верно, если в классе ровно один молчун. Пусть их не менее двух.
Выделим молчуна A и его друзей — болтунов B1, … ,Bk.
Для оставшихся n – 1 – k учеников утверждение верно, т.е. можно выделить группу M, в которой каждый болтун дружит с нечётным числом молчунов и в M входит не менее 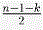 учеников. учеников.
Предположим, что болтуны B1, … ,Bm дружат с нечётным числом молчунов из M, а Bm + 1, … ,Bk — с чётным числом.
Тогда, если 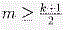 , то добавим к группе M болтунов B1, … ,Bm, , то добавим к группе M болтунов B1, … ,Bm,
а если 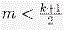 , то добавим к группе M болтунов Bm + 1, … ,Bk и молчуна A. , то добавим к группе M болтунов Bm + 1, … ,Bk и молчуна A.
В обоих случаях мы получим группу учеников, удовлетворяющую условию задачи. 
Задача 3. Многогранник описан около сферы.
Назовём его грань большой, если проекция сферы на плоскость грани целиком попадает в грань.
Докажите, что больших граней не больше 6.
Решение:
Пусть R — радиус шара.
Сопоставим каждой большой грани часть граничной сферы шара, расположенную в конусе, вершиной которого служит центр шара, а основанием — проекция шара на эту грань.
Указанная часть сферы является «сферической шапочкой» (то есть частью сферы, лежащей по одну сторону от секущей сферу плоскости) высоты 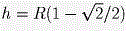 . .
По известной формуле площадь такой «шапочки» равна 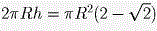 . .
Так как указанные «шапочки» не перекрываются, сумма их площадей не превосходит площади сферы.
Обозначив количество больших граней через n, получим 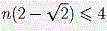 , то есть , то есть 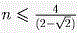 . .
Решение заканчивается проверкой того, что 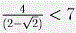 . .
Примечание. Легко видеть, что у куба шесть больших граней.
Поэтому приведенная в задаче оценка числа больших граней является точной. 
Задача 4. Существуют ли действительные числа a, b и c такие,
что при всех действительных x и y выполняется неравенство
|x + a| + |x + y + b| + |y + c| |x| + |x + y| + |y| ?
Решение:
Ответ: Нет.
Предположим, что такие числа a, b и c существуют.
Выберем x 0 и y 0 такие, что x + a ≥ 0, x + y + b ≥ 0, y + c ≥ 0.
Тогда разность между левой и правой частями равна a + b + c.
А если взять x то эта разность будет равна – a – b – c.
Таким образом, с одной стороны, a + b + c 0, с другой a + b + c Противоречие. 
Задача 5. Клетки квадрата 50 × 50 раскрашены в четыре цвета.
Докажите, что существует клетка, с четырех сторон от которой (то есть сверху, снизу, слева и справа)
имеются клетки одного с ней цвета.
Решение:
Предположим, что клетки квадрата n × n удалось раскрасить таким образом, что для любой клетки с какой-то стороны от неё нет клетки одного с ней цвета.
Рассмотрим тогда все клетки одного цвета и в каждой из них нарисуем стрелочку в том из четырёх направлений, в котором клетки того же цвета нет.
Тогда на каждую клетку «каёмки» нашего квадрата будет указывать не более одной стрелки.
Так как клеток каёмки всего 4n – 4, то и клеток каждого цвета не более 4n – 4.
С другой стороны, каждая из n² клеток нашего квадрата раскрашена в один из четырёх цветов, то есть n² ≤ 4(4n – 4).
Для решения задачи теперь достаточно заметить, что последнее неравенство неверно при n = 50.
Несложно убедиться, что оно неверно при всех n ≥ 15, и, следовательно,
утверждение задачи верно уже в квадрате 15 × 15 — а заодно и в любом большем квадрате. 
Задача 6. Для бесконечного множества значений многочлена,
существует более одной целой точки, в которой принимаются эти значения.
Докажите, что существует не более одного целого значения многочлена,
принимаемого ровно в одной целой точке.
Решение:
Из условия следует, что многочлен имеет ненулевую степень.
Докажем, что данный многочлен p(x) имеет чётную степень, а его график имеет вертикальную ось симметрии.
Не умаляя общности, мы можем считать старший коэффициент многочлена p(x) положительным
(иначе многочлен можно заменить на – p(x)).
Если p(x) имеет нечётную степень, то при всех достаточно больших по абсолютной величине x он возрастает, и, следовательно, может принимать более чем в одной целой точке лишь конечное число значений.
Поэтому степень p(x) чётна.
Тогда при больших положительных x многочлен возрастает, а при больших по модулю отрицательных x — убывает, и, следовательно, все достаточно большие значения, которые он принимает более чем в одной целой точке, он принимает ровно дважды.
Упорядочим эти значения: a1 2 k больший, а yk — меньший прообраз ak.
Таким образом, p(xk) = p(yk) = ak.
Мы докажем, что при достаточно больших k сумма xk + yk постоянна.
Для этого рассмотрим два старших коэффициента p(x): p(x) = axn + bxn – 1 + …
Тогда 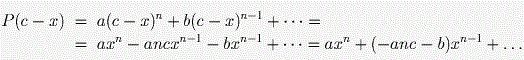
(многоточия скрывают члены не выше (n – 2)-й степени; кроме того, мы воспользовались чётностью n).
Заметим, что коэффициенты при xn у многочленов p(x) и p(c – x) совпадают; что же до коэффициентов при xn – 1, то существует единственное значение c (а именно c0 = – 2b/(an)), при котором совпадают и они.
Если c c0, то p(x) – p(c – x) — многочлен степени n – 1 с положительным старшим коэффициентом, следовательно, при достаточно больших x его значения положительны.
Поэтому при достаточно больших k xk + yk 0 + 0.1 (иначе будет p(yk) p(c0 + 0.1 – xk) p(xk)). Если, наоборот, c 0, то p(x) – p(c – x) — многочлен степени n – 1 с отрицательным старшим коэффициентом, значения которого при достаточно больших x отрицательны.
Поэтому при достаточно больших k xk + yk c0 – 0.1. Но xk + yk — целые числа, поэтому, начиная с некоторого k, все они равны: xk + yk = c. Но тогда многочлены p(x) и p(c – x) совпадают почленно (если не все их коэффициенты совпадают, то при больших x знак p(x) – p(c – x) должен совпадать со знаком первого ненулевого коэффициента этой разности; с другой стороны, среди xk есть сколь угодно большие числа, и для них p(c – xk) = p(yk) = p(xk).)
Итак, p(x) = p(c – x) при всех вещественных x.
Тогда любое значение, принимаемое в целой точке x ≠ c/2, принимается и в точке c – x ≠ x.
Поэтому единственное значение, которое может приниматься ровно в одной целой точке — это p(c/2), да и то, если только c/2 – целое.
Всероссийская олимпиада по математике | Международная олимпиада по математике Школьная олимпиада с решением
|
Олимпиадные задания по математике для учащихся 1-11 классов с решением и ответами:
Главная | 1 класс | 2 класс |3 класс | 4 класс | 5 класс | 6 класс | 7 класс | 8 класс | 9 класс | 10 класс | 11 класс
|
Задачи по математике 11 класс  
|
Олимпиадные задания по математике 11 класс.
Варианты заданий с решением и ответами : 1 вариант | 2 вариант | 3 вариант
Задача 1 :
Каждое ребро куба покрашено в красный или чёрный цвет.
При этом каждая грань куба имеет хотя бы одно чёрное ребро.
Какое наименьшее количество рёбер могло быть покрашено в чёрный цвет?
A - 2 / B - 3 / C - 4 / D - 5 / E - 6
Задача 2 :
Когда в Москве полдень, в Чикаго 3 часа утра. Когда в Москве 3 часа утра,
в Петропавловске-Камчатском полдень.
Сколько времени в Чикаго, когда в Петропавловске-Камчатском 3 часа утра?
A - 18 часов / B - 6 часов / C - 9 часов / D - 15 часов / E - 21 час
Задача 3 :
Пусть выражение a x b обозначает сумму цифр в произведении a b.
Тогда (15 x 10) x (15 10) =
A - 5 / B - 6 / C - 9 / D - 10 / E - 150
Задача 4 :
На плоскости через данную точку провели 8 прямых линий.
Какое наибольшее число прямых углов могло при этом образоваться?
A - 4 / B - 8 / C - 12 / D - 16 / E - 20
Задача 5 :
В одной комнате сидят 9 человек, и их средний возраст - 25 лет.
В другой комнате сидят 11 человек, и их средний возраст - 45 лет.
Каков средний возраст всех 20 человек?
A- 40 / B - 36 / C - 35 / D - 32 / E - 30
Задача 6 :
12 мальчиков и 8 девочек являются членами математического клуба.
Каждую неделю в клуб принимают двух новых девочек и одного мальчика.
Сколько будет членов в клубе в тот день,
когда мальчиков и девочек станет поровну?
A - 20 / B - 24 / C - 28 / D - 32 / E - 36
Задача 7 :
Улитка взбирается на ветку длиной 10 дм.
За день она поднимается на 4 дм, а за ночь сползает вниз на 3 дм.
Через сколько дней улитка достигнет конца ветки?
A - 7 / B - 8 / C - 9 / D - 10 / E - 11
Задача 8 ;
Белоснежка раздавала семи гномам грибы.
Каждый следующий гном получал на один гриб больше предыдущего,
а все вместе они получили 707 грибов.
Сколько грибов получил последний гном?
A - 98 / B - 100 / C - 101 / D - 104 / E - 107
Задача 9 ;
Ребро куба равно 1. Муха ползает по рёбрам этого куба, не проходя по одному ребру дважды
(но, возможно, проходя несколько раз через одну вершину).
Какой самый длинный путь она может проползти?
A - 6 / B - 8 / C - 9 / D - 10 / E - 12
Задача 10 ;
Четыре футбольные команды сыграли круговой турнир.
За победу начисляется 3 очка, за ничью 1 очко. Команды набрали 5, 3, 3 и 2 очка.
Сколько было ничьих?
A - 5 / B - 4 / C - 3 / D - 2 / E - 1
Ответы к задачам олимпиады :
1 - B
2 - C
3 - C
4 - D
5 - B
6 - D
7 - A
8 - D
9 - C
10 - D
Задача 1.
Докажите, что ребус: ЗАДАЧА + ЗАДАЧА = ТУРНИР не имеет решений.
Решение:
Сложение А + А должно быть выполнено в трех различных разрядах, при этом результаты записываются тремя различными буквами У, Н и Р.
Но это невозможно, так как А + А может принимать только два разных значения эта сумма является либо некоторым четным числом (если нет переноса из предыдущего разряда), либо следующим за ним нечетным (если есть перенос единицы из предыдущего разряда).
Переноса двух единиц быть не может.

Задача 2.
У Васи и Пети по 55 гирь весом 1, 2, ...... , 55 кг.
Они по очереди подкладывают свои гири каждый на свою чашу двухчашечных весов причем первым ходит Вася.
Петя выигрывает, если разность масс гирь на чашах окажется равной 50 кг.
Сможет ли он этого добиться?
Решение:
1. Петя может просто повторять ходы Васи.
В какой-то момент Вася вынужден будет сходить гирей 50 кг и немедленно проиграет.
2. Петя откладывает в сторону свою 50-килограммовую гирю и ходит как угодно остальными гирями.
В конце игры Вася выложит все гири, а Петя все, кроме 50-килограммовой.
Следовательно, чаша Васи будет весить на 50 кг тяжелее.

Задача 3.
Пусть S(n) сумма цифр числа n.
Найдите все n, для которых

Решение:
Ответ. Таких n не существует.
Доказательство. Все n слагаемых в левой части дают одинаковый остаток при делении на 3, совпадающий с остатком от деления на 3 самого числа n.
Перебирая три различных случая, получаем, что остаток от деления левой части на 3 равен либо 0, либо 1.
Но правая часть число 2000000 при делении на 3 дает в остатке 2.

Задача 4.
В треугольнике ABC ∠ A = 3 ∠ C. Точка D на стороне BC обладает тем свойством, что ∠ ADC = 2 ∠ C. Доказать, что AB + AD = BC.
Решение:
Продолжим отрезок BA за точку A и отложим на нем отрезок AE = AD.
Заметим, что ∠ EAC = 180 – ∠ BAC = 180 – 3 ∠ C, поэтому треугольники ADC и AEC равны (по сторонам AC, AD = AE и углу между ними).
Отсюда находим углы треугольника AEC: ∠ AEC = ∠ ADC = 2 ∠ C, ∠ ACE = ∠ C, т.е. ∠ BCE = 2 ∠ C, поэтому треугольник BEC равнобедренный.
Таким образом, AB + AD = AB + AE = BE = BC.

Задача 5.
Имеется n дискеток и n этикеток, раскрашенные в несколько цветов.
Дубль это дискета, к которой приклеена этикетка того же цвета.
Докажите, что можно добиться того, что все дубли будут одного цвета.
Решение:
1. Наклеим сначала этикетки на дискетки в произвольном порядке.
Предположим, что у нас образовались дубли нескольких различных цветов.
Возьмем по одной дискетке-дублю двух разных цветов и обменяем их этикетки. После этого каждая из дискеток перестанет быть дублем, так что общее число дублей уменьшится на 2.
Далее будем повторять эту операцию до тех пор, пока дублей различных цветов не останется.
2. Докажем нужный факт индукцией по числу дискеток (при этом можно даже не обращать внимание на соответствие цветов дискеток и этикеток!).
База индукции (одна дискетка) очевидна.
Переход: если все k + 1 дискеток одноцветны, то и доказывать нечего.
Если же есть дискетки разных цветов, то возьмем одну из них и наклеим на нее этикетку другого цвета, а для остальных k дискеток применим предположение индукции.
Решения задач первого этапа Всесибирской олимпиады школьников 2012-2013 г. по математике 7 класс 7.1. Килограмм мяса с костями стоит 165 рублей, килограмм мяса без костей стоит 240 рублей, а килограмм костей стоит 40 рублей. Сколько граммов костей в килограмме мяса с костями? Ответ. 375 граммов. Решение. Пусть в килограмме мяса с костями x кило костей. Тогда 40x2401−x=165 , откуда x=0,375 . 7.2. В семье трое братьев. Известно, что Коля родился на следующий год после того года, когда до рождения младшего из братьев оставалось 5 лет, а Ваня родился на два года раньше, чем среднему исполнилось 3 года. Сейчас Пете 10 лет. Сколько лет Ване и Коле? Ответ. Ване сейчас 9 лет, а Коле – 13 лет. Решение. Из второго условия про Ваню следует, что он младше среднего брата на 1 год, поэтому Ваня – младший. Коля же старше младшего на 4 года, поэтому он старший. Значит, Петя – средний, тогда Ване сейчас 9 лет, а Коле – 13 лет.
7.3. От шоссе к четырем поселкам A,B,C,D последовательно отходят четыре дороги. Известно, что путь по дороге/шоссе/дороге от A до B равен 9 км, от A до C — 13 км, от B до C — 8 км, от B до D — 14 км. Найдите длину пути по дороге/шоссе/дороге от A до D. Ответ объясните. Ответ: 19 км. Решение. Сложим пути от A до C и от B до D. Тогда участок шоссе от поворота на B до поворота на C будет сосчитан дважды, а участки шоссе от поворота на A до поворота на B и от поворота на C до поворота на D, а также все четыре дороги от шоссе до посёлков — по одному разу. Поэтому, если мы теперь вычтем из получившейся суммы путь из B в C, в полученной разности будут учтены по одному разу все три отрезка шоссе и подъездные дороги до A и D, то есть как раз то, что составляет путь из A в D. Стало быть, длина этого пути равна 13+14–8 = 19 км. 7.4. Какой может быть сумма цифр числа, делящегося на 7? Ответ. Любое натуральное число, больше, либо равное 2. Решение. Заметим, что числа 21 и 1001 делятся на 7, суммы их цифр равны 3 и 2 соответственно. Значит, чтобы получить сумму цифр, равную чётному числу n , нужно взять число, десятичная запись которого состоит из n 2 групп цифр 1001. Соответственно, чтобы получить сумму цифр, равную нечётному числу 2n1 , нужно взять число, десятичная запись которого состоит из n 2 −1 групп цифр 1001 и одной группы цифр 21. Сумма же цифр, равная 1, получиться не может, потому что степени десятки на 7 не делятся. 7.5. На клетчатой доске размера 5 на 5 отмечено несколько клеток так, что каждый квадрат 3 на 3 клетки содержит ровно одну отмеченную клетку. Какое количество клеток может быть отмечено? Ответ. Любое от 1 до 4.
Решение. Ясно, что хоть одна клетка быть должна. С другой стороны, четыре угловых квадрата 3 на 3 полностью покрывают квадрат 5 на 5, и каждый из них содержит ровно 1 отмеченную клетку, следовательно, всего отмеченных клеток не более 4. Примеры для количеств от 1 до 4 приведены на рисунке.
Игра «Пенальти». 6-7 класс. Решения. 27.03.2013.
1.Вася сбегает по эскалатору, едущему вниз, не пропуская ни одной ступеньки. Скорость Васи вдвое больше скорости эскалатора. Пока Вася ехал, он пробежал 80 ступеней. Сколько ступеней он пробежит, если будет сбегать по неподвижному эскалатору? (120. Пока Вася бежал, эскалатор спустился на 80:2=40 ступеней. Значит, его длина равна 80+40=120 ступеням. Их Вася и пробежит, сбегая по неподвижному эскалатору.)
2. Бумага расчерчена на клеточки со стороной 1. Ваня вырезал из неё по клеточкам прямоугольник и нашёл его площадь и периметр. Таня отобрала у него ножницы и со словами «Смотри, фокус!» вырезала с краю прямоугольника по клеточкам квадратик, выкинула квадратик и объявила: «Теперь у оставшейся фигуры периметр такой же, какая была площадь прямоугольника, а площадь — как был периметр!» Ваня убедился, что Таня права. Приведите пример такого прямоугольника и такого квадрата. (3´10 или 4´6 без квадратика 2´2– см. рис.)
3. Год проведения нынешнего Кубка делится на его номер: 2013:3=671. Сколько ещё будет Кубков (если он и дальше будет проводиться ежегодно), для номеров которых это свойство тоже будет выполнено? (13. Пусть N - номер Кубка. Тогда год его проведения равен (2013−3)+N=2010+N. Пусть год проведения делится на номер, т.е. 2010+N делится на N. Значит, 2010 делится на N. Количество натуральных делителей числа 2010 равно τ(2010)= τ(2×3×5×67)=24=16, т.к. каждый из простых множителей (2, 3, 5, 67) либо входит, либо не входит в разложение на простые множители числа 2010. Но Кубки под номерами 1, 2 и 3 (нынешний) нами не должны учитываться. Значит, ещё будет 16-3=13 подобных Кубков.)
4.Все четырёхзначные числа, цифры которых различны и стоят в порядке возрастания, выписали друг за другом - снова в порядке возрастания. Какое число стоит на 16-м месте? (Числа в нашем списке идут группами 1234-1239, 1245-1249, 1256-1259 и т.д. В первой группе 6 чисел, во второй - 5, в третьей – 4, значит, нам нужно 16-6-5-4=1-е число четвёртой группы, т.е. 1267.)
5. Отметьте на прямой пять различных точек таким образом, чтобы для любых двух из них нашлась такая третья (тоже отмеченная), что одна из этих трёх точек является серединой отрезка между двумя другими. (Отметим на числовой прямой точки с координатами 0, 2, 3, 4, 6. Перебором легко проверяется выполнение требуемого условия.)
6. Дано равенство М∙А∙Ш∙А=О∙Т∙Л∙И∙Ч∙Н∙И∙Ц∙А. Маша смогла заменить каждую букву на свою цифру так, что равенство стало верным. Какая цифра соответствует букве А? (Разные буквы - разные цифры, одинаковые буквы – одинаковые числа). (0. В равенстве использовано 10 различных букв, поэтому одна из них соответствует цифре 0. Тогда одно из произведений равно нулю, поэтому и другое произведение равно нулю, то есть цифра ноль должна быть в обеих частях равенства. А – единственная буква, которая есть в обеих частях равенства.)
7. Во сколько раз увеличилось положительное число, если оно увеличилось на 400%? (в пять раз)
8. Саша пригласил Петю в гости, сказав, что живёт в 10-м подъезде в квартире № 333, а этаж сказать забыл. Подойдя к дому, Петя обнаружил, что дом девятиэтажный. На какой этаж ему следует подняться? (На каждом этаже число квартир одинаково, номера квартир в доме начинаются с единицы.) (На 3-й этаж. Если на этаже не более трёх квартир, то в десяти подъездах их не более, чем 10×9×3=270, то есть в 10-м подъезде квартиры № 333 не будет. Если на этаже не менее пяти квартир, то уже в девяти подъездах будет не менее, чем 9×9×5=405 квартир, то есть искомая квартира будет не в десятом подъезде. Значит, квартир на этаже 4, в первых девяти подъездах 9×9×4=324 квартиры. Тогда в десятом подъезде квартиры начинаются с 325-й. На втором этаже они начнутся с 329-й, на третьем - с 333-й. Таким образом, Пете нужно подняться на третий этаж.)
9. Бочку можно наполнить, если в неё налить 6 маленьких, 3 средних и 1 большое ведро воды, или же 2 маленьких, 1 среднее и 3 больших ведра воды. А сколько только больших вёдер потребуется для наполнения бочки?(4 ведра. Из условий задачи следует, что вместимость двух больших ведер равна общей вместимости 4 маленьких и двух средних ведер. Следовательно, вместимость одного большого ведра равна вместимости 2 маленьких и одного среднего ведра. Тогда их можно заменить (во втором способе наполнения) 1 большим ведром, и в бочку, таким образом, вмещается 4 больших ведра воды.)
10.На ста карточках написаны различные целые числа от 1 до 100 (по одному числу на каждой карточке). Какое минимальное число карточек нужно взять не глядя, чтобы среди них обязательно нашлись три карточки, сумма чисел на которых кратна трём? (5. Среди любых пяти целых чисел есть либо три числа с одинаковыми остатками при делении на 3, и их сумма делится на 3, либо три числа с тремя различными остатками - их сумма тоже делится на 3. Если взять не более четырёх карточек, три искомых могут и не найтись, например, если два числа делятся на 3, а два других по модулю 3 имеют одинаковые ненулевые остатки (1 или 2).)
11. Карлсон съедает 40 кг конфет за 8 дней, а вместе с Малышом – за 5 дней. За сколько дней Малыш съест 30 кг конфет? (10 дней. За один день Карлсон съедает 40:8=5 кг конфет, за 5 дней – 25 кг. Значит, Малыш за 5 дней съедает 40–25=15 кг конфет, а за день – 15:5=3 кг. Поэтому 30 кг конфет Малыш съест за 30:3=10 дней.)
12. Треугольник периметра 1 разделен на треугольники так, как показано на рисунке. Оказалось, что периметры всех девяти маленьких треугольников равны. Найдите, чему равны эти периметры. (1/3. Раскрасим треугольники в шахматном порядке (см.рис.), тогда суммарный периметр трёх чёрных треугольников 3Р на 1 (периметр большого треугольника) меньше суммарного периметра 6Р шести белых треугольников. Из полученного уравнения найдём, что Р=1/3.)
13. На дороге длиной 40 км стоят несколько (больше одного) пеньков. Первый турист идёт пешком со скоростью 5 км/ч, и на каждом пеньке отдыхает одинаковое целое число часов. Второй турист едет на велосипеде со скоростью 8 км/ч и отдыхает на каждом пеньке в два раза дольше, нежели первый турист. Вышли и пришли туристы одновременно. Сколько могло быть пеньков? (3. Если бы туристы нигде не останавливались, то один прошёл бы всю дорогу за 8 часов, а другой за 5. Принимая во внимание то, что один отдыхал на пеньках в 2 раза больше другого, получаем уравнение 5+2x=8+x, где x - продолжительность сидения первого туриста на всех пеньках, откуда получаем, что x=3. Так как пеньков больше 1, а на каждом пеньке туристы сидят целое число часов, то пеньков может быть только 3.)
14.В мешке 100 шаров - чёрных, белых и серых. Количество чёрных шаров больше, чем удвоенное количество белых; утроенное количество белых шаров больше, чем учетверённое количество серых; утроенное количество серых шаров больше количества чёрных. Сколько шаров чёрного цвета в мешке? (55. Пусть серых шаров хотя бы 20, тогда белых хотя бы 27, тогда чёрных хотя бы 55, что противоречит условию на их общее количество. Пусть серых шаров не больше чем 18, тогда чёрных не больше 53, тогда белых не больше 26, и опять противоречие с тем, что всего шаров 100. Значит, серых ровно 19. Тогда чёрных не больше, чем 56, откуда белых не больше 27 (из первого условия), и не меньше, чем 25 (из суммы 100). Если белых 27, то чёрных 54, что не подходит в условие, если 25, то количества серых и белых шаров не удовлетворяют нужному соотношению. Таким образом, белых шаров 26, а чёрных 100-26-19=55, что удовлетворяет условиям задачи.)
15. У 15 ребят есть 8 одинаковых яблок. Разрешается резать яблоко на равные части, но не более, чем на 5 частей. Как разделить яблоки между ребятами так, чтобы каждому досталось поровну? (Разные яблоки можно резать на разное число частей.)(Разрежем пять яблок на три равные части каждое, три яблока — на пять равных частей каждое, и дадим каждому из ребят по 1/3+1/5 яблока.)
16. Учительница пересадила Вовочку с первого ряда на второй, Ванечку – со второго ряда на третий, а Машеньку – с третьего ряда на первый. Причём средний возраст учеников, сидящих на первом ряду, увеличился на неделю, сидящих во втором ряду – увеличился на две недели, а сидящих на третьем ряду – уменьшился на четыре недели. Известно, что на первом и втором рядах сидят по 12 человек. Сколько человек сидит на третьем ряду? (9. Общее увеличение суммы возрастов детей, сидящих на первых двух рядах равно 1∙12 + 2∙12 = 36 недель, но, так как сумма возрастов во всём классе осталась прежней, это же увеличение есть уменьшение суммы возрастов сидящих на третьем ряду. Отсюда получаем, что на третьем ряду сидит 36/4=9 человек.)