Просмотр содержимого документа
«Решение логарифмических неравенств»
Логарифмические неравенства (параграф 20)
- Рассмотрите примеры решения неравенств в параграфе 20.
Нам нужно научиться решать неравенства, подобные тем, которые рассмотрены в задачах 1, 2 и 3 параграфа 20.
Пример № 1. (перепишите обязательно, можно без словесных пояснений)
Решить неравенство 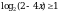
| 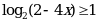
Представим число 1 в виде логарифма с тем же основанием, что и в выражении слева от знака = : Т.е. 1 = 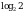 , перепишем неравенство: , перепишем неравенство: 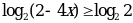 ; ;
Основание логарифма 2, т.е. оно больше единицы, значит, функция возрастает. Вспоминаем теорему (см. стр. 100 учебника), по которой, т.к. основания логарифмов равны, мы можем перейти к сравнению подлогарифмических функций. А т.к. основание логарифма больше единицы, и функция поэтому возрастает, то знак неравенства (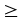 ) остается тем же! ) остается тем же! 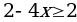
Решим: 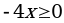 / : (-4) / : (-4)
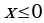 - это решение неравенства - это решение неравенства
| ОДЗ: 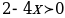 (по определению логарифма, подлогарифмическая функция должна быть строго больше нуля) (по определению логарифма, подлогарифмическая функция должна быть строго больше нуля)
Теперь решим неравенство: 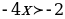 / : (-4) (при делении неравенства на отрицательное число, знак меняется, т.е. был / : (-4) (при делении неравенства на отрицательное число, знак меняется, т.е. был 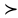 , а стал , а стал 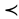 !!!! !!!!
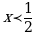 - это ОДЗ - это ОДЗ
|
Теперь необходимо на числовой прямой отметить точки 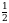 и
и  .
.
Заштриховать область ОДЗ :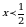 (с наклоном штрихов в одну сторону, например, вправо) и область, которая является решением самого неравенства :
(с наклоном штрихов в одну сторону, например, вправо) и область, которая является решением самого неравенства : 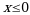 ( с наклоном штрихов в другую сторону). В итоге у вас получится область, заштрихованная «крестиками» - это и есть решение логарифмического неравенства!
( с наклоном штрихов в другую сторону). В итоге у вас получится область, заштрихованная «крестиками» - это и есть решение логарифмического неравенства!
Для нашего примера: Ответ: 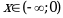 .
.
Пример № 2. (перепишите обязательно, можно без словесных пояснений)
Решить неравенство 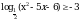
| 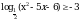
Представим число (-3) в виде логарифма с основанием 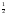 : : 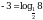 . . Перепишем неравенство: 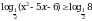
Основание логарифма меньше единицы, т.е. функция убывает, значит, при переходе к сравнению подлогарифмических функций, знак неравенства будет меняться на противоположный! (Был  , а станет , а станет  ): ): 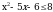 , перенесём 8 влево и решим неравенство: , перенесём 8 влево и решим неравенство: 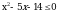 . .
Сначала решим уравнение 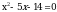 : : 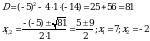
Теперь эти 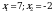 надо отметить на числовой прямой. Получится три интервала. Нужно узнать знаки этих интервалов. Т.к. графиком функции надо отметить на числовой прямой. Получится три интервала. Нужно узнать знаки этих интервалов. Т.к. графиком функции 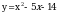 является парабола, с ветками, направленными вверх, то знаки расположатся так: + - + является парабола, с ветками, направленными вверх, то знаки расположатся так: + - + Нам нужен интервал со знаком « - », т.к. 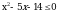 ( ( 0 – меньше либо равно нуля). 0 – меньше либо равно нуля). Т.е. решение данного неравенства: 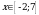
| ОДЗ: 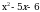  
Решим уравнение: 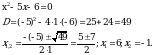
Теперь эти 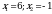 надо отметить на числовой прямой. Получится три интервала. Нужно узнать знаки этих интервалов. Т.к. графиком функции надо отметить на числовой прямой. Получится три интервала. Нужно узнать знаки этих интервалов. Т.к. графиком функции 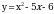 является парабола, с ветками, направленными вверх, то знаки расположатся так: + - +: является парабола, с ветками, направленными вверх, то знаки расположатся так: + - +: Нам нужны интервалы со знаком «+», т.к 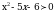 ( (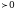 - больше нуля). - больше нуля). Т.е. решение данного неравенства: 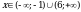 - это ОДЗ - это ОДЗ |
Теперь на одной числовой прямой отмечаем точки -1; 6; -2 и 7.
Заштриховываем область ОДЗ : 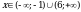 (с наклоном штрихов в одну сторону, например, вправо) и область, которая является решением самого неравенства :
(с наклоном штрихов в одну сторону, например, вправо) и область, которая является решением самого неравенства : 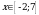 ( с наклоном штрихов в другую сторону). В итоге у вас получится область, заштрихованная «крестиками» - это и есть решение логарифмического неравенства!
( с наклоном штрихов в другую сторону). В итоге у вас получится область, заштрихованная «крестиками» - это и есть решение логарифмического неравенства!
Для нашего примера: Ответ: 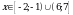 .
.
Эти два примера перепишите, пояснения писать не обязательно, а числовые прямые с заштрихованными ответами – обязательны!!!!! Я вышлю на всякий случай в вотсап, если вдруг вы забыли, как это делается.
- посмотрите видео (лучше сначала 2 и 3, а потом 1):
Видео 1
Видео 2
Видео 3
- Решите в тетради номера: 355, 357 и примеры ниже (№ 1, 2, 3, 4 из обоих столбцов):

Задания прислать до ______ (включительно).






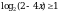
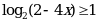
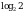 , перепишем неравенство:
, перепишем неравенство: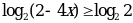 ;
;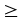 ) остается тем же!
) остается тем же!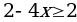
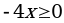 / : (-4)
/ : (-4)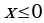 - это решение неравенства
- это решение неравенства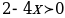 (по определению логарифма, подлогарифмическая функция должна быть строго больше нуля)
(по определению логарифма, подлогарифмическая функция должна быть строго больше нуля)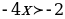 / : (-4) (при делении неравенства на отрицательное число, знак меняется, т.е. был
/ : (-4) (при делении неравенства на отрицательное число, знак меняется, т.е. был 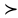 , а стал
, а стал 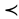 !!!!
!!!!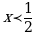 - это ОДЗ
- это ОДЗ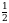 и
и  .
.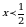 (с наклоном штрихов в одну сторону, например, вправо) и область, которая является решением самого неравенства :
(с наклоном штрихов в одну сторону, например, вправо) и область, которая является решением самого неравенства : 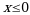 ( с наклоном штрихов в другую сторону). В итоге у вас получится область, заштрихованная «крестиками» - это и есть решение логарифмического неравенства!
( с наклоном штрихов в другую сторону). В итоге у вас получится область, заштрихованная «крестиками» - это и есть решение логарифмического неравенства! 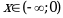 .
.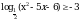
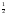 :
: 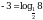 .
.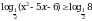
 , а станет
, а станет  ):
):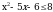 , перенесём 8 влево и решим неравенство:
, перенесём 8 влево и решим неравенство: 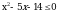 .
.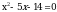 :
: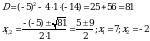
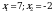 надо отметить на числовой прямой. Получится три интервала. Нужно узнать знаки этих интервалов. Т.к. графиком функции
надо отметить на числовой прямой. Получится три интервала. Нужно узнать знаки этих интервалов. Т.к. графиком функции 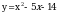 является парабола, с ветками, направленными вверх, то знаки расположатся так: + - +
является парабола, с ветками, направленными вверх, то знаки расположатся так: + - +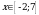
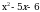

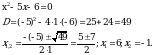
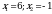 надо отметить на числовой прямой. Получится три интервала. Нужно узнать знаки этих интервалов. Т.к. графиком функции
надо отметить на числовой прямой. Получится три интервала. Нужно узнать знаки этих интервалов. Т.к. графиком функции 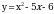 является парабола, с ветками, направленными вверх, то знаки расположатся так: + - +:
является парабола, с ветками, направленными вверх, то знаки расположатся так: + - +: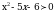 (
(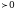 - больше нуля).
- больше нуля).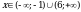 - это ОДЗ
- это ОДЗ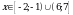 .
.










