Решение стереометрических задач.

Решение по планиметрической стереометрический задачи. Часть I

Урок

Цель:

Образовательная:

повторить навыки решений планиметрических и стереометрических задач для применениях их в повседневной жизни;

Развивающая:

• способствовать формированию умений; сравнивать, обобщать, выделять главное, переносить знания в новую ситуацию, анализировать условие задачи, составлять модель решения;

• способствовать развитию умений и навыков применять математические знания к решению практических задач, ориентироваться в простейших геометрических конструкциях.

Воспитательная:

содействовать воспитанию интереса к математике, активности, мобильности, умения общаться.

Задачи урока:

• выявить уровень подготовки учащихся по геометрии по данной теме, систематизировать полученные знания с помощью приема «Кластер»;

• помочь в развитии и самореализации творческих способностей личности;

• обучить приемам организации интеллектуального труда;

• научить учащихся находить главное;

• продолжить воспитание у учащихся уважительного отношения друг к другу, чувства товарищества, культуры общения, чувства ответственности.

1. Оргмомент

2. Задание для обсуждения «Фермерский дом»

Текст для чтения.

Здесь вы видите фото фермерского домика с крышей в форме пирамиды.

Вопросы для обсуждения (Анализируем содержания текста):

Примеры заданий:

Перед вами изображение математической модели крыши данного дома с добавленными единицами измерения.

Чердак, обозначенный, как ABCD в модели, представляет собой квадрат. Поддерживающие крышу балки являются ребрами блока (прямоугольной призмы) EFGHKLMN. Точка Е – середина балки AT, точка F – середина балки BT, точка G – середина балки CT, а точка H – середина балки DT соответственно. Все ребра пирамиды имеет длину 12 метров.

Вычислите площадь чердака ABCD.

Площадь чердака ABCD = м².

ОЦЕНКА ОТВЕТА:

Вопрос 1

ЦЕЛЬ ВОПРОСА:

Область математического содержания: Изменение и зависимости Контекст: Научный

Познавательная деятельность:

Воспроизведение, определения, вычисления

Ответ принимается полностью:

Площадь чердака представляющий собой квадрат вычисляется по формуле

где и получаем

1 балл

Ответ не принимается:

Если другие ответы

Если ответ отсуствует : 0 балл

Вычислите длину EF, одного из горизонтальных ребер блока. Длина EF = м.

Характеристики задания и система оценивания.

ЦЕЛЬ ВОПРОСА:

Область математического содержания: Пространство и форма Контекст: Профессиональный

Познавательная деятельность: Установление связей и интеграция информации для решения задачи.

Ответ принимается полностью:

Длина один из горизонтальных ребер блока EF вычисляется применением свойства средней линии треугольника

где и получаем

1 балл

Ответ не принимается:

Если другие ответы

Если ответ отсуствует

0 балл

«Базовый» ассортимент производителя гаражей включает в себя модели только с одним окном и одной дверью.

Дима выбрал следующую модель из «базового» ассортимента. Расположение на ней окна и двери показано справа.

На приведенных ниже рисунках показано, как «основные» модели выглядят сзади. Только один из этих рисунков соответствует модели, выбранной Димой.

Какую модель выбрал Дима? Обведите A, B, C или D.

ЦЕЛЬ ВОПРОСА:

Описание: Использовать пространственные способности для соотнесения двух трехмерных моделей.

Область математического содержания: Пространство и форма Контекст: Профессиональный

Познавательная деятельность: Интерпретировать

На двух приведенных ниже планах показаны размеры (в метрах) гаража, выбранного Димой.

1,00

2,40

0,50 1,00 ^{2,00 1,00 0,50} 6,00

Вид спереди Вид сбоку

Крыша сделана из двух одинаковых прямоугольных секций.

Вычислите площадь всей крыши. Приведите решение.

2,40

ГАРАЖ: ОЦЕНКА ОТВЕТА НА ВОПРОС 2

ЦЕЛЬ ВОПРОСА:

Описание:

Интерпретировать план и вычислить площадь треугольника, используя теорему Пифагора или измерения.

Область математического содержания: Пространство и форма

Контекст: Профессиональный

4. Задание «Юрта»

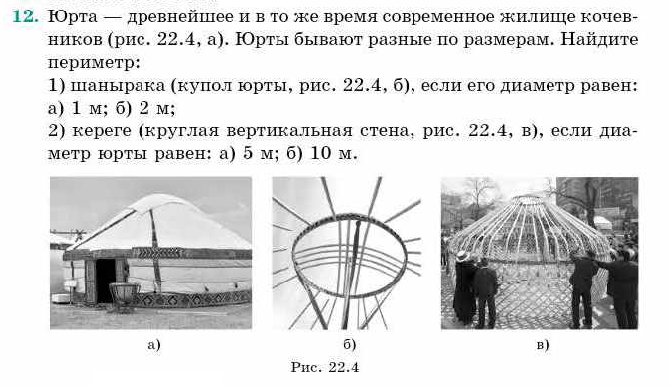
Здесь вы видите фото юрты с крышей в форме конуса, и её частей. Семье (фамилии) при строительстве юрты необходимо приобрести войлок для стен и крыши.

Юрта — древнейшее и в то же время современное жилище кочевников

Юрты бывают разные по размерам.

1) шанырака (купол юрты, б)

2) керете (круглая вертикальная стена, в),

Примеры заданий:

Перед вами изображение математической модели юрты с добавленными единицами измерения.

Технические характеристики войлока.

Ширина рулона: 2м

Длина рулона: 6 м.

Вопрос 1 «Юрта»

Рассчитайте сколько квадратных метров войлока понадобится для покрытия:

а) стен

б) крыши

Вопрос 2 «Юрта»

Сколько рулонов войлока понадобится для покрытия всей юрты.