Решение треугольников

Решение треугольников

Геометрия

9 класс

Решение треугольников состоит в нахождении неизвестных сторон и углов по известным его сторонам и углам.

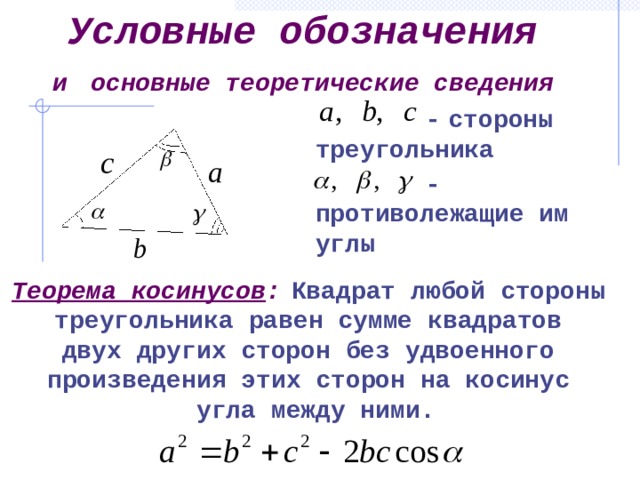
Условные обозначения и основные теоретические сведения

- стороны треугольника

- противолежащие им углы

Теорема косинусов : Квадрат любой стороны

треугольника равен сумме квадратов

двух других сторон без удвоенного

произведения этих сторон на косинус

угла между ними.

Теорема синусов: Стороны треугольника

пропорциональны синусам противолежащих

углов

Теорема о сумме углов треугольника:

Сумма углов треугольника равна 180 0

* для любого острого угла выполняются равенства ;

** для любого угла выполняются равенства

Типы задач

1. Решение треугольников по стороне и двум углам.

2. Решение треугольников по двум сторонам и углу между ними.

3. Решение треугольников по трём сторонам.

4. Решение треугольников по двум сторонам и углу, лежащему напротив одной из них.

1. Решение треугольника по стороне и двум углам.

Дано:

Найти:

?

?

Решение: 1.

?

2. По теореме синусов находим стороны:

3.

Ответ:

2. Решение треугольников по двум сторонам и углу между ними.

Дано:

Найти:

?

?

Решение: 1. По теореме косинусов

найдём неизвестную сторону с:

?

2. По теореме косинусов находим косинус неизвестного угла

По таблице Брадиса находим угол:

3.

Ответ:

3. Решение треугольников по трём сторонам.

Дано:

Найти:

?

Решение: 1. По теореме косинусов

найдём меньший из углов:

?

?

По таблице Брадиса находим угол:

2. По теореме косинусов найдём средний из углов:

По таблице Брадиса находим угол:

3.

Ответ:

4. Решение треугольников

по двум сторонам и углу,

лежащему напротив одной из них.

Дано:

Найти:

?

?

?

Решение: 1. По теореме синусов

найдём :

Этому значению синуса соответствуют два угла, т.к.

. Значит и .

Рассмотрим сначала I случай:

2. Находим

По теореме синусов находим третью сторону:

Рассмотрим II случай:

3. Находим

4. По теореме синусов находим третью сторону:

Ответ: 1.

2.