Разработка урока по теме «Решение задач по теме: "Радиоактивные превращения"» (Физика, 9 класс)
Класс: 9
Продолжительность: 45 минут
Тип урока: Урок практического применения знаний
Цели урока (в соответствии с ФГОС):
Образовательная цель: Отработать навыки решения задач на вычисление периодов полураспада, активности радиоактивных веществ и количества оставшихся ядер.
Развивающая цель: Развивать логическое мышление, способность анализировать физические процессы и применять формулы для решения задач.
Воспитательная цель: Формировать ответственное отношение к изучению физики, интерес к научно-исследовательской деятельности.
Задачи урока:
Повторить основные понятия радиоактивных превращений (период полураспада, активность, дезинтеграция).
Научить применять формулы для расчета:
Количество оставшихся ядер после определенного времени;
Активность радиоактивного вещества;
Время распада.
Выполнить практические задачи разного уровня сложности.
Оборудование и материалы:
Таблица основных формул по теме "Радиоактивные превращения";
Доска и маркеры;
Индивидуальные карточки с задачами для учеников;
Проектор (для демонстрации примеров решений);
Калькуляторы для каждого ученика.
Структура урока:
1. Организационный момент (3 мин)
Приветствие учащихся.
Объявление темы и целей урока.
Мотивационный вопрос: "Как можно предсказать, сколько времени потребуется для того, чтобы радиоактивное вещество стало безопасным?"
2. Актуализация знаний (7 мин)
Повторение теоретического материала:
Что такое радиоактивный распад?
Какие виды радиоактивных превращений вы знаете?
Что такое период полураспада?
Что такое активность радиоактивного вещества?
Основные формулы:
N=N0⋅2−t/T, где N — количество оставшихся ядер, N0 — начальное количество ядер, t — время, T — период полураспада.
A=A0⋅2−t/T, где A — активность через время t, A0 — начальная активность.
T1/2= 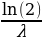 , где λ — постоянная распада.
, где λ — постоянная распада.
Устные вопросы:
Если период полураспада равен 10 лет, сколько времени потребуется, чтобы количество ядер уменьшилось в 8 раз?
Что больше: активность 1 грамма радия или активность 1 грамма урана? Почему?
3. Решение типовых задач (15 мин)
Задача 1 (простая):
Период полураспада радиоактивного элемента составляет 5 лет. Сколько ядер останется через 15 лет, если первоначально их было 64×1020?
Решение:
Используем формулу N=N0⋅2−t/T.
t=15 лет, T=5 лет.
N=64×1020⋅2−15/5=64×1020⋅2−3=64×1020⋅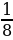 =8×1020.
=8×1020.
Ответ: 8×1020 ядер.
Задача 2 (средней сложности):
Активность радиоактивного вещества составляет 16Бк при t=0. Через сколько времени она уменьшится до 2Бк, если период полураспада равен 4 часа?
Решение:
Используем формулу A=A0⋅2−t/T.
A=2Бк, A0=16Бк, T=4 часа.
2=16⋅2−t/4.
2−t/4=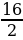 =81=2−3.
=81=2−3.
−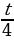 =−3.
=−3.
t=12 часов.
Ответ: 12 часов.
Задача 3 (сложная):
Масса радиоактивного вещества m0=8г. Через какое время масса уменьшится до 0.5г, если период полураспада равен 2 года?
Решение:
Масса вещества пропорциональна количеству ядер. Используем формулу m=m0⋅2−t/T.
m=0.5г, m0=8г, T=2 года.
0.5=8⋅2−t/2.
2−t/2=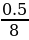 =
=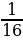 =2−4.
=2−4.
−2t=−4.
t=8 лет.
Ответ: 8 лет.
4. Самостоятельная работа (10 мин)
Ученики получают индивидуальные карточки с задачами разного уровня сложности. Примеры:
Легкая:
Период полураспада радиоактивного элемента T=8 лет. Сколько ядер останется через 24 года, если первоначально их было 128×1020?
Средняя:
Активность радиоактивного вещества составляет 64Бк при t=0. Через сколько времени она уменьшится до 8Бк, если период полураспада равен 3 часа?
Сложная:
Масса радиоактивного вещества m0=16г. Через какое время масса уменьшится до 1г, если период полураспада равен 6 месяцев?
5. Подведение итогов (5 мин)
Обсуждение результатов самостоятельной работы.
Ответы на вопросы учащихся.
Выставление оценок за правильность выполнения задач.
6. Домашнее задание (5 мин)
№ ... из учебника (задачи на вычисление периода полураспада, активности и количества оставшихся ядер).
Подготовить презентацию о practical applications радиоактивных превращений в медицине или энергетике (по выбору).
Ожидаемые результаты:
Учащиеся смогут правильно применять формулы для расчета периодов полураспада, активности и количества оставшихся ядер.
Они научатся решать задачи разного уровня сложности.
Ученики проявят интерес к практическому применению радиоактивных превращений.






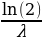 , где λ — постоянная распада.
, где λ — постоянная распада.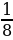 =8×1020.
=8×1020.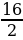 =81=2−3.
=81=2−3.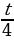 =−3.
=−3.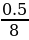 =
=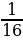 =2−4.
=2−4.









