Решение задач по теме: "Строки с пропущенными значениями. "

Строки с пропущенными значениями

Решение задач

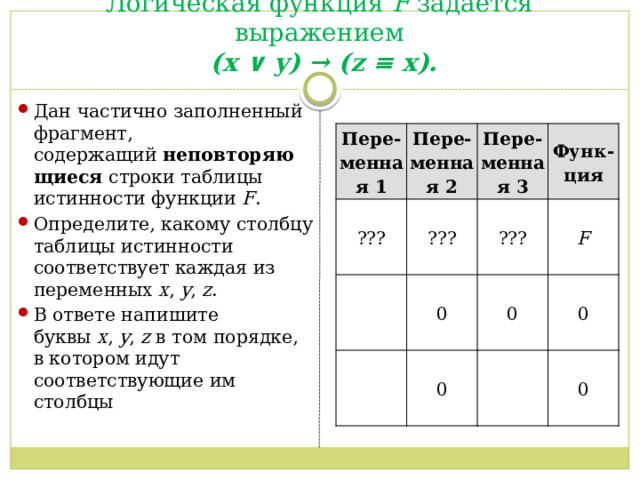
Логическая функция  F  задаётся выражением  (x ∨ y) → (z ≡ x).

• Дан частично заполненный фрагмент, содержащий  неповторяющиеся  строки таблицы истинности функции  F .
• Определите, какому столбцу таблицы истинности соответствует каждая из переменных  x ,  y ,  z .
• В ответе напишите буквы  x ,  y ,  z  в том порядке, в котором идут соответствующие им столбцы

Пере-менная 1

Пере-менная 2

???

???

Пере-менная 3

Функ-ция

???

0

F

0

0

0

0

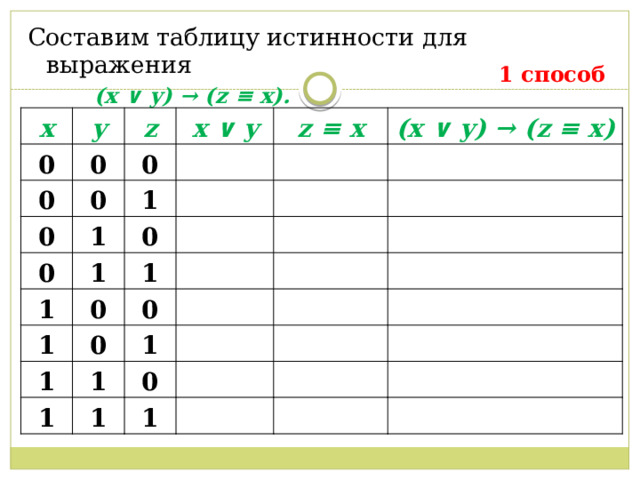
Составим таблицу истинности для выражения

(x ∨ y) → (z ≡ x).

1 способ

x

y

0

0

z

0

x ∨ y

0

0

0

1

z ≡ x

1

0

1

1

(x ∨ y) → (z ≡ x)

0

0

1

1

0

0

1

1

1

1

0

1

1

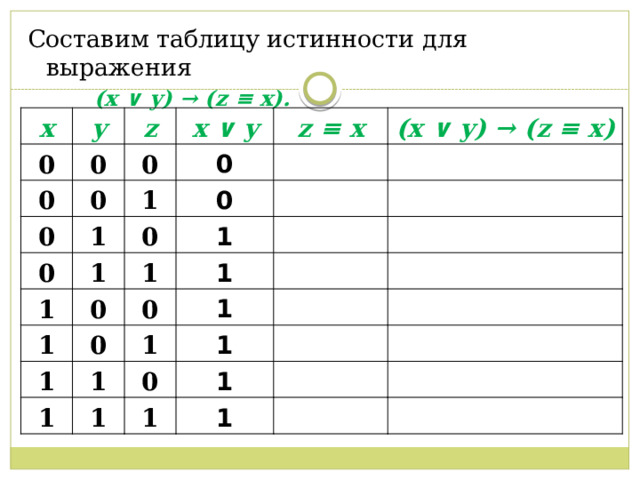
Составим таблицу истинности для выражения

(x ∨ y) → (z ≡ x).

x

y

0

0

z

0

0

x ∨ y

0

0

1

0

0

1

z ≡ x

0

(x ∨ y) → (z ≡ x)

0

1

1

1

0

1

1

1

1

0

0

1

1

1

1

1

0

1

1

1

1

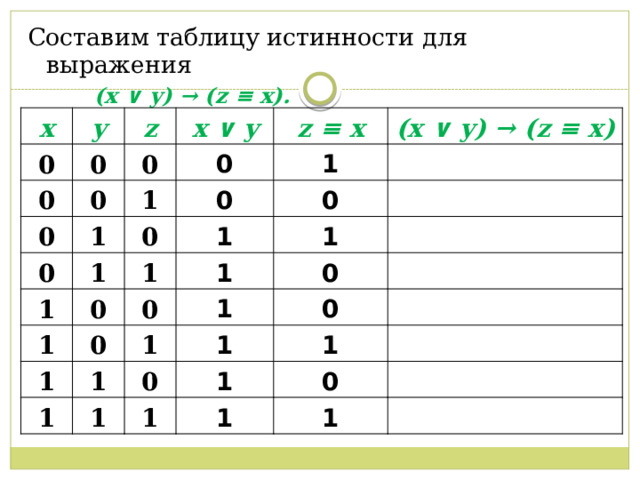
Составим таблицу истинности для выражения

(x ∨ y) → (z ≡ x).

x

0

y

0

z

0

x ∨ y

0

0

0

1

0

z ≡ x

1

0

1

0

1

0

1

(x ∨ y) → (z ≡ x)

0

1

0

1

1

1

0

0

1

1

1

1

1

0

1

1

0

0

1

1

1

1

0

1

1

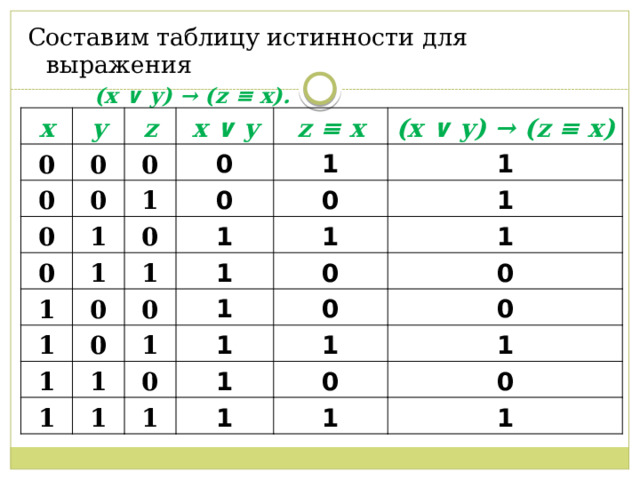
Составим таблицу истинности для выражения

(x ∨ y) → (z ≡ x).

x

y

0

0

z

0

0

x ∨ y

0

0

1

0

1

0

z ≡ x

1

0

1

(x ∨ y) → (z ≡ x)

0

1

0

1

1

1

1

0

0

1

1

1

0

1

1

1

1

1

1

0

0

1

0

0

1

0

1

1

1

0

1

1

0

1

1

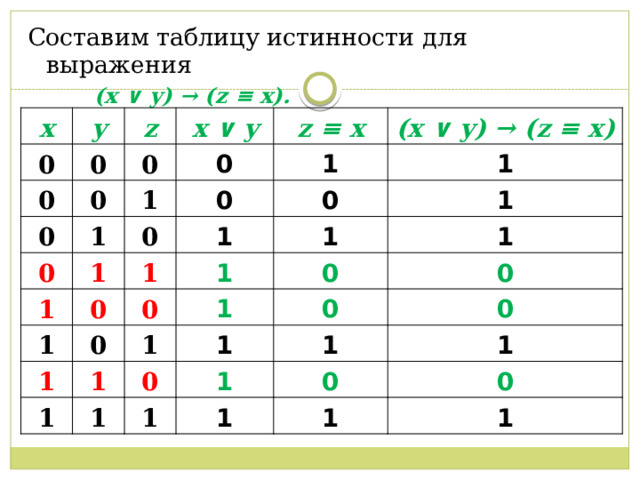
Составим таблицу истинности для выражения

(x ∨ y) → (z ≡ x).

x

y

0

0

z

0

0

x ∨ y

0

0

1

0

1

0

z ≡ x

1

0

1

(x ∨ y) → (z ≡ x)

0

1

0

1

1

1

1

0

0

1

1

1

0

1

1

1

1

1

1

0

0

1

0

0

1

0

1

1

1

0

1

1

0

1

1

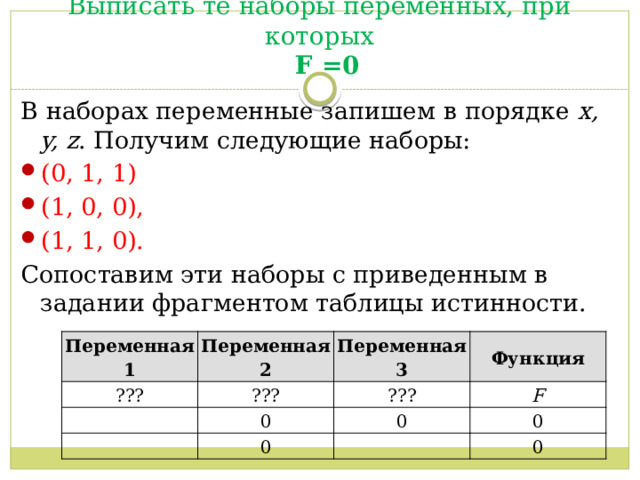
Выписать те наборы переменных, при которых F =0

В наборах переменные запишем в порядке  х, y, z . Получим следующие наборы:

• (0, 1, 1)
• (1, 0, 0),
• (1, 1, 0).

Сопоставим эти наборы с приведенным в задании фрагментом таблицы истинности.

Переменная 1

???

Переменная 2

Переменная 3

???

Функция

???

0

F

0

0

0

0

Выписать те наборы переменных, при которых F =0

• (0, 1, 1)
• (1, 0, 0),
• (1, 1, 0).

Второй столбец таблицы может соответствовать только переменной  z , поскольку переменная  y  принимает нулевое значение только в одном наборе.

Переменная 1

Переменная 2

???

Переменная 3

???

Функция

???

0

F

0

0

0

0

Выписать те наборы переменных, при которых F =0

• (0, 1, 1)
• (1, 0, 0),
• (1, 1, 0).

Первый столбец таблицы соответствует переменной  x , и в первом столбце первой строки стоит 1.

Переменная 1

???

Переменная 2

Переменная 3

???

Функция

???

0

F

0

0

0

0

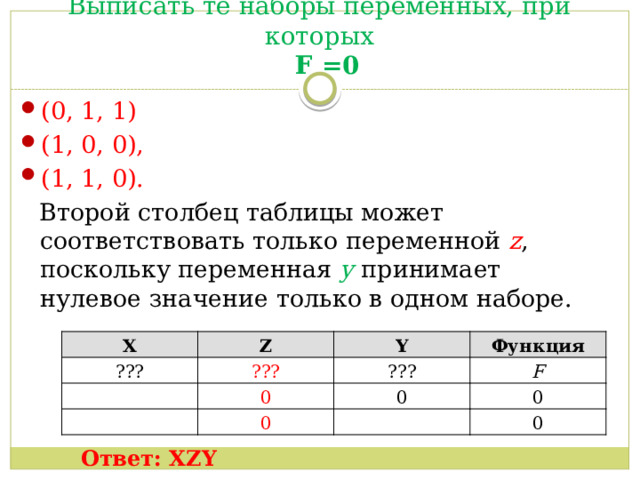
Выписать те наборы переменных, при которых F =0

• (0, 1, 1)
• (1, 0, 0),
• (1, 1, 0).

Второй столбец таблицы может соответствовать только переменной  z , поскольку переменная  y  принимает нулевое значение только в одном наборе.

X

???

Z

Y

???

Функция

???

0

F

0

0

0

0

Ответ: XZY

  (x ∨ y) → (z ≡ x) данная импликация принимает значение 0 тогда и только тогда, когда 

2 способ

Пусть x = 0, тогда y = z = 1. В первой строке нет двух единиц, значит, x = 1, и эта переменная находится в первом столбце. Тогда первая строка имеет вид 1 0 0 .

Переменная 1

???

Переменная 2

Переменная 3

???

Функция

0

???

F

0

0

0

0

  (x ∨ y) → (z ≡ x) данная импликация принимает значение 0 тогда и только тогда, когда 

2 способ

Пусть x = 0, тогда y = z = 1. В первой строке нет двух единиц, значит, x = 1, и эта переменная находится в первом столбце. Тогда первая строка имеет вид 1 0 0 .

x

1

Переменная 2

Переменная 3

0

Функция

0

0

F

0

0

0

0

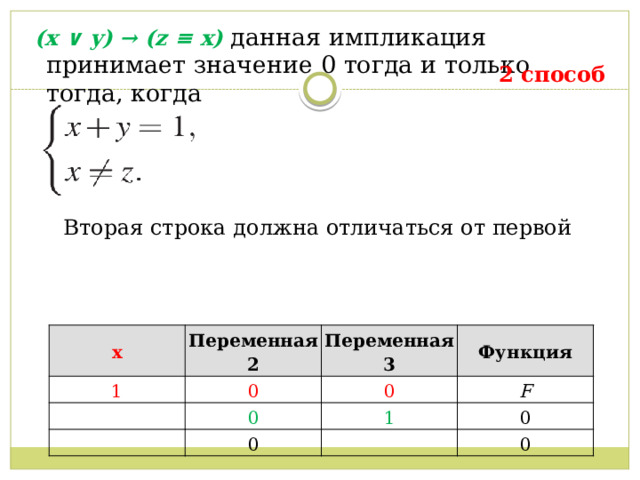
  (x ∨ y) → (z ≡ x) данная импликация принимает значение 0 тогда и только тогда, когда 

2 способ

Вторая строка должна отличаться от первой

x

1

Переменная 2

Переменная 3

0

Функция

0

0

F

1

0

0

0

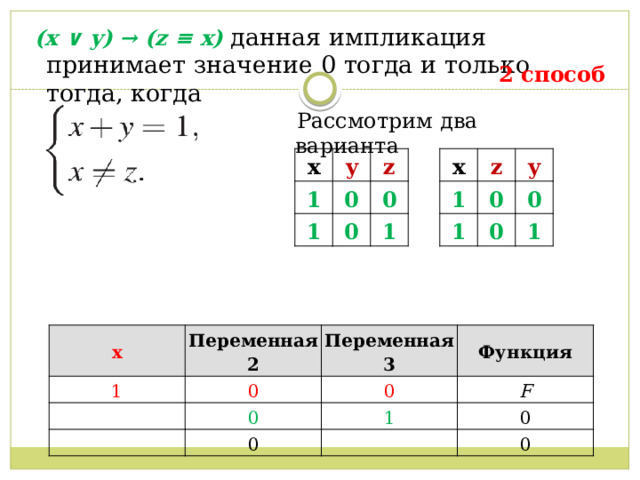
  (x ∨ y) → (z ≡ x) данная импликация принимает значение 0 тогда и только тогда, когда 

2 способ

Рассмотрим два варианта

x

x

y

z

1

1

0

1

0

y

1

z

0

0

0

0

1

1

x

1

Переменная 2

Переменная 3

0

Функция

0

0

0

1

F

0

0

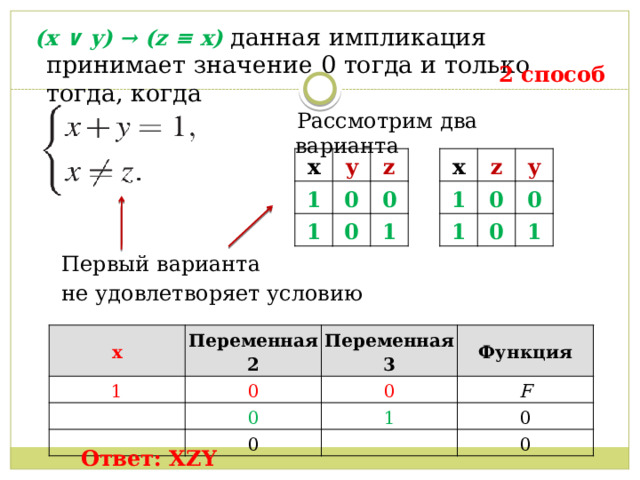
  (x ∨ y) → (z ≡ x) данная импликация принимает значение 0 тогда и только тогда, когда 

2 способ

Рассмотрим два варианта

x

x

z

y

1

1

z

1

0

y

1

0

0

0

0

0

1

1

Первый варианта

не удовлетворяет условию

x

1

Переменная 2

Переменная 3

0

Функция

0

0

F

0

1

0

0

Ответ: XZY

((x or y) TrueTablePrint( t,0 ); https:// www.onlinegdb.com " width="640"

Составим таблицу истинности для выражения

(x ∨ y) → (z ≡ x).

3 способ

##

uses school; {uses - раздел подключения модулей}

var T:= TrueTable((x,y,z)-((x or y)

TrueTablePrint( t,0 );

https:// www.onlinegdb.com

((x or y) TrueTablePrint( t ); https:// www.onlinegdb.com " width="640"

Составим таблицу истинности для выражения

(x ∨ y) → (z ≡ x).

3 способ

##

uses school;

var T:= TrueTable((x,y,z)-((x or y)

TrueTablePrint( t );

https:// www.onlinegdb.com

f(a, …, e))  возвращает матрицу типа boolean, содержащую таблицу истинности для заданной функции  n -аргументов (где  n  не больше 5); Процедура  TrueTablePrint(a)  выводит таблицу истинности, полученную посредством функции TrueTable; Процедура  TrueTablePrint(a, f)  выводит таблицу истинности, полученную посредством функции TrueTable. Параметр f позволяет фильтровать выводимые строки: при   f = 0 выводятся только строки, в которых значение функции равно False, при f = 1 – только строки, в которых оно равно True " width="640"

Конструкции языка, используемые при построении логических высказываний.

• Расширение a.Imp(b) возвращает результат операции импликации  a → b , допускается запись  a
• Функция  TrueTable((a, …, e) - f(a, …, e))  возвращает матрицу типа boolean, содержащую таблицу истинности для заданной функции  n -аргументов (где  n  не больше 5);
• Процедура  TrueTablePrint(a)  выводит таблицу истинности, полученную посредством функции TrueTable;
• Процедура  TrueTablePrint(a, f)  выводит таблицу истинности, полученную посредством функции TrueTable. Параметр f позволяет фильтровать выводимые строки: при   f = 0 выводятся только строки, в которых значение функции равно False, при f = 1 – только строки, в которых оно равно True

Составим таблицу истинности для выражения

(x ∨ y) → (z ≡ x).

3 способ

print ("x y z")

for x in range( 0 , 2 ):

for y in range( 0 , 2 ):

for z in range( 0 , 2 ):

if not ((x or y)

print (x, y, z)

https:// www.onlinegdb.com/online_python_compiler

Получим следующие наборы:

• (0, 1, 1)
• (1, 0, 0),
• (1, 1, 0).
• Сопоставим эти наборы с приведенным в задании фрагментом таблицы истинности.

Переменная 1

Переменная 2

???

Переменная 3

???

Функция

???

0

F

0

0

0

0

Получим следующие наборы:

• (0, 1, 1)
• (1, 0, 0),
• (1, 1, 0).
• Первая строка таблицы может соответствовать набору (1, 0, 0), следовательно, первый столбец таблицы соответствует переменной  x , и в первом столбце первой строки стоит 1.

Переменная 1

Переменная 2

???

Переменная 3

???

Функция

???

0

F

0

0

0

0

Получим следующие наборы:

• (0, 1, 1)
• (1, 0, 0),
• (1, 1, 0).
• Второй столбец таблицы может соответствовать только переменной  z , поскольку переменная  y  принимает нулевое значение только в одном наборе. Тогда третий столбец соответствует переменной  y .

Переменная 1

???

Переменная 2

Переменная 3

???

Функция

???

0

F

0

0

0

0

Ответ: XZY