Решение задач с помощью уравнений

Тема урока: Решение задач с помощью уравнений

Класс: 6

Цель: сформировать представление как можно решить задачи при помощи уровнений

образовательные: усовершенствовать умения решать уравнения; закрепить умения решать задачи на составление уравнений; развивать умение составлять уравнения по условию задачи, сформировать умения учащихся решать более сложных задач на проценты с помощью уравнения;

развивающие: развить логическое мышление учащихся, умение рассуждать;

воспитательные: формировать самостоятельность, внимательность, аккуратность, учится преодолевать трудности.

Оборудование: учебник

Ход урока.

1.Организационный момент.

2. Проверка домашнего задания

3. Актуализация знаний.

Индивидуальная карточка.

№1

Петя прочитал книгу за три дня. За первый день прочитал на 20 % больше, чем за второй, а за третий день – 20 страниц. Всего в книге 108 страниц. Сколько страниц прочитал Петя за второй день?

4. Изучение нового материала

Работа с классом.

1. Что такое уравнение? (Уравнение – это равенство содержащее переменную.)

2. Что такое корень уравнения? (Это значение переменной, при котором уравнение обращается в верное равенство.)

3. Что значит решить уравнение? (Это значит найти все его корни или доказать что их нет.)

4. Какой алгоритм решения задач с помощью уравнений?

(1. Составить схему, используя условие;

2. ввести неизвестную;

3. составить уравнение;

4. решить уравнение.)

Учитель подчеркивает, что правильно составленное уравнение значительно облегчает решение задачи на проценты.

Рассмотрим основные типы задач, для решения которых составляют уравнения.

3. Формирование умений

№1

Дочка в 4 раза младше матери. Сколько лет матери, если она старше дочери на 27 лет?

Решение:

4х-х=27

3х=9

х=9

Ответ: дочери 9 лет, а матери 36.

№2

За 3 ручки и 5 карандашей заплатили 6 грн 85 коп. Сколько стоит одна ручка и сколько один карандаш, если карандаш дешевле ручки на 55 коп.?

Решение:

3х+5(х-55)=685

3х+5х-275=685

8х=960

х=120

Ответ: 120 коп стоимость одной ручки, 65 коп стоимость одного карандаша.

№3

В одном шкафу было на 25% меньше книг, чем в другом. Когда в первый шкаф положили 17 книг, а из второго взяли 25, то в обоих шкафах книг стало поровну. Сколько книг было в каждом шкафу сначала?

Решение:

х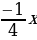  +17=х-25

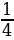 х=42

х=168

Ответ: в одном шкафу 168 книг, в другом шкафу 126 книг.

№4

У Ани в 3 раза больше денег, чем у Коли. Когда Аня купила ручку за 5,5 грн, а Петя купил карандаш за 1 грн 25 коп, то у Ани денег стало в 2 раза больше, чем у Пети. Сколько денег было у детей изначально?

Решение:

3х-5,5=2(х-1,25)

3х-2х=-2,5+5,5

х=3

Ответ: изначально у Пети было 3 грн, а у Ани – 9 грн.

Проверить умение учащихся решать задачи на составление уравнения.

Работа с разноуровневыми карточками.

Решение задач по выбору (откорректировать выбор учащихся по уровню сложности) (у каждого ученика карточка с задачами)

Высокий уровень ( на 12 баллов)

№1

Протяженность реки Енисей на 308 км меньше, чем протяженность реки Лена, и составляет 93% протяженности реки Лена. Найдите протяженность каждой реки.

Решение:

х-0,93х=308

0,07х=308

х=308:0,07

х=4400

Ответ: протяженность реки Лена 4400 км, а реки Енисей – 4092 км.

№2

За 1007 гривен было куплено ролики, самокат и велосипед; цена самокат составляет 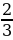  цены велосипеда; цена роликов составляет  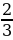 цены самоката. Сколько заплачено за каждую вещь.

Решение:

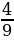 х+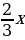  +х=1007

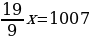
х=1007: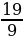

х=477

Ответ: стоимость роликов 212 грн, стоимость самоката 318 грн, а велосипеда – 477 грн.

Достаточный уровень (на 9 баллов)

№1

8 телят и 5 овец съели 835 кг корма. За все время каждому теленку дали на 28 кг корма больше, чем овце. Сколько корма съел каждый теленок, сколько съела каждая овца?

Решение:

8(х+28)+5х=835

8х+5х=835-224

13х=611

х=47

Ответ: одной овце давали вдень 47 кг корма, а одному теленку – 75 кг корма.

№2

На двух полках 72 книги. Когда с первой полки переставили на вторую 14 книг, то книг на полках стало поровну. Сколько книг стояло на каждой полке первоначально?

Решение:

(х-14)+(х+14)=72

Cредний уровень (на 6 баллов)

№1

Кусок полотна в 124 м надо разрезать на две части так, чтобы длина одной части была на 12 м больше другой. По сколько метров полотка будет в каждой части?

Решение:

х+х+12=124

2х=112

х=112:2

х=56

Ответ: длина одной части 56 м, а другой 68 м

№2

На автостоянке 24 автомобиля, причем легковых автомобилей в 3 раза больше, чем грузовых. Сколько грузовых автомобилей на автостоянке?

3х+х=24

4х=24

х=6

Ответ: на автостоянке 6 грузовиков.

Задача на дополнительные 12 баллов

Владелец магазина поднял цену на музыкальные диски на 25 %, но из-за такой высокой цены спрос на товар упал. Это заставило владельца уменьшить новую цену на 25 %, после чего стоимость диска составила 45 грн. Какова была начальная цена музыкальных дисков?

Решение:

х+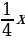  -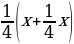  =45

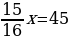
х=48

Ответ: начальная цена музыкальных дисков 48 грн.

Учитель дает 3 минуты, чтобы дети определились с уровнем. А затем вызывает ребенка, который выбрал средний уровень, к доске и решает вместе с ним. Дети, у которых возникли трудности при решении, решают вместе с ними. Вторую задачу из среднего уровня ученики пытаются решить самостоятельно.

Проверка. На доске ученики кратко записывают решение задач высокого уровня. Уравнения, написанные к задачам среднего и достаточного уровней, учащиеся комментируют с места.

1. Подведение итогов урока

2. Рефлексия

1. Домашнее задание

Повторить §32 решить № 1,2.