Решение задач второй части ЕГЭ "Механика"

Решение задач части 2 ЕГЭ «Механика»

Учитель: Елена Анатольевна Фокина

Рекомендуемый алгоритм решения задач по динамике

Задача 1

Полусферическая чаша радиусом 25 см вращается вокруг вертикальной оси, проходящей

через ее центр. Горошина находится на внутренней поверхности сферы. Коэффициент

трения горошины о поверхность равен 0.7. Радиус- вектор, проведенный к горошинке из центра

сферы, образует угол 60 градусов с вертикалью. С какой частотой должна вращаться

чаша, чтобы горошина начала подниматься вверх по поверхности чаши?

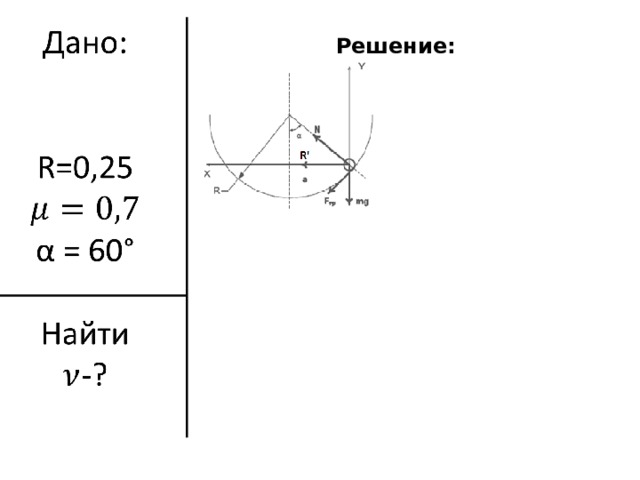
Решение:

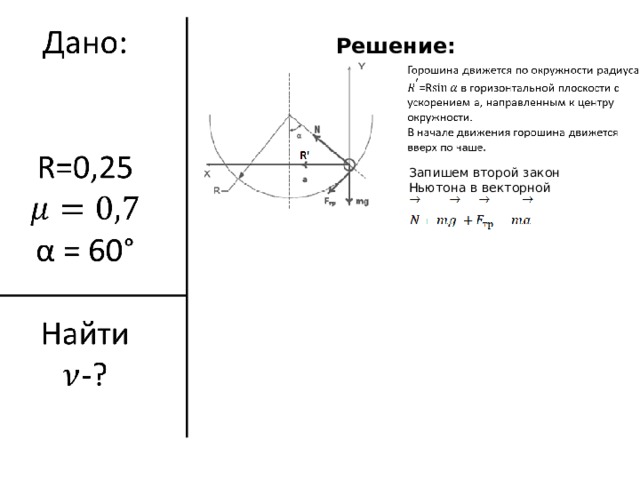
Решение:

Запишем второй закон Ньютона в векторной форме:

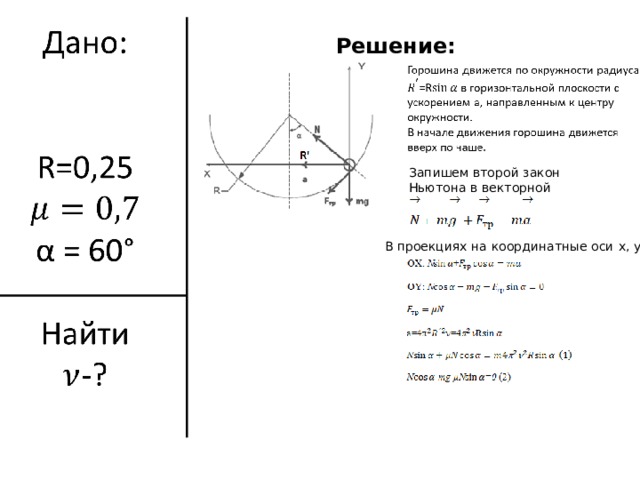
Решение:

Запишем второй закон Ньютона в векторной форме:

В проекциях на координатные оси x , y :

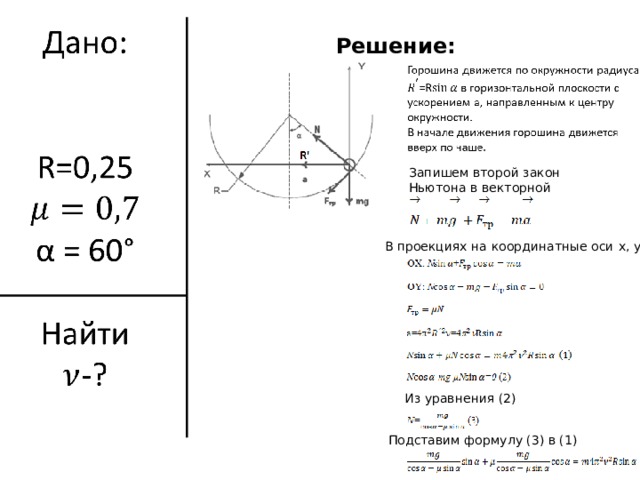
Решение:

Запишем второй закон Ньютона в векторной форме:

В проекциях на координатные оси x , y :

Из уравнения (2)

Подставим формулу (3) в (1)

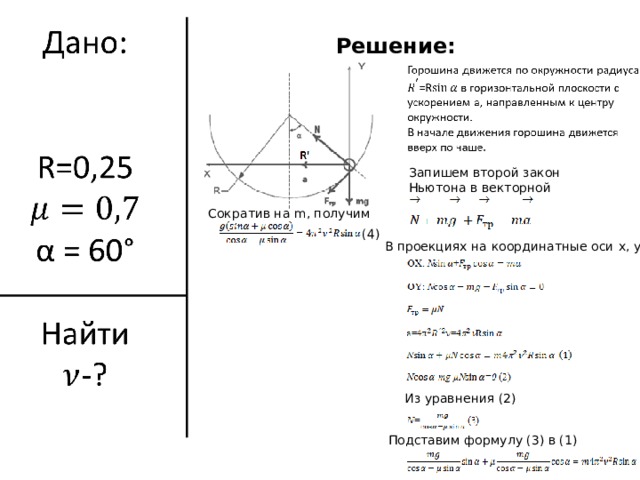
Решение:

Запишем второй закон Ньютона в векторной форме:

Сократив на m , получим

(4)

В проекциях на координатные оси x , y :

Из уравнения (2)

Подставим формулу (3) в (1)

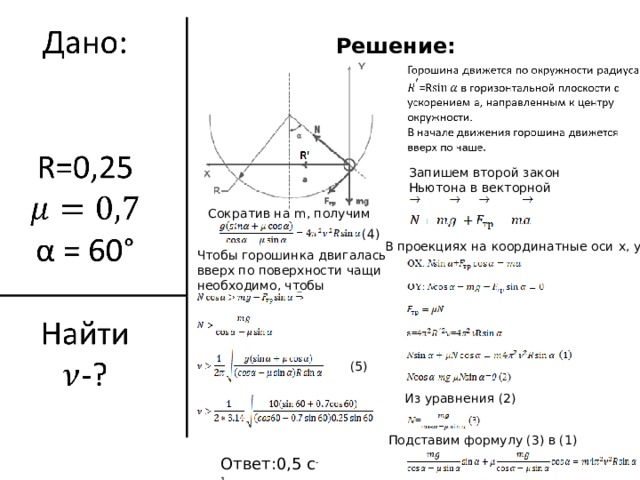
Решение:

Запишем второй закон Ньютона в векторной форме:

Сократив на m , получим

(4)

В проекциях на координатные оси x , y :

Чтобы горошинка двигалась вверх по поверхности чащи необходимо, чтобы

(5)

Из уравнения (2)

Подставим формулу (3) в (1)

Ответ:0,5 с -1

Рекомендуемый алгоритм решения задач по законам сохранения в механике

Задача 2

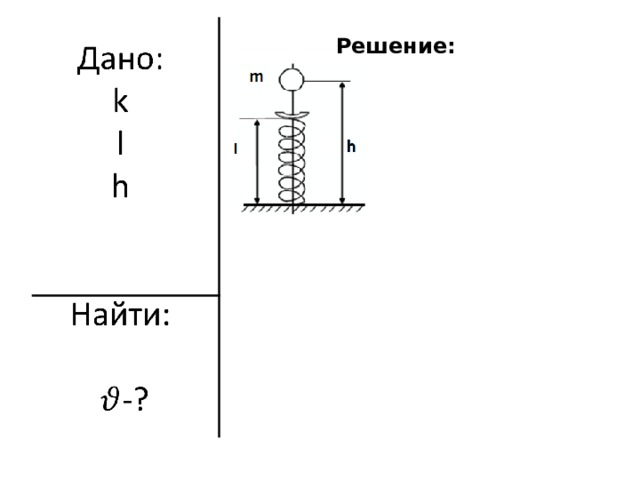
На невесомую вертикально расположенную пружину с жесткостью k и длиной l с высоты h падает шарик массой m (см. рисунок). Какую максимальную скорость будет иметь шарик при движении вниз?

Решение:

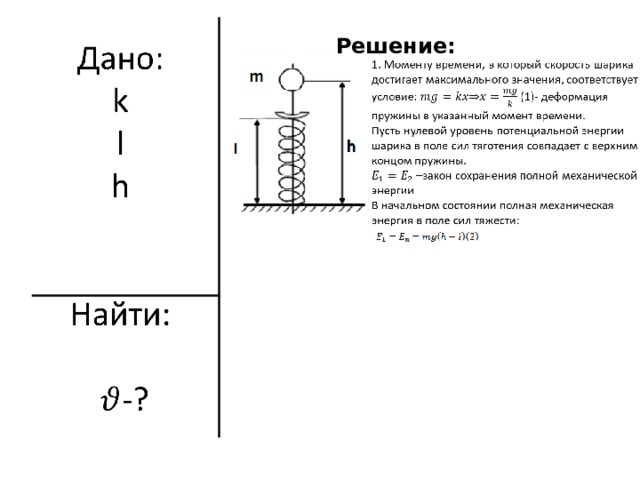
Решение:

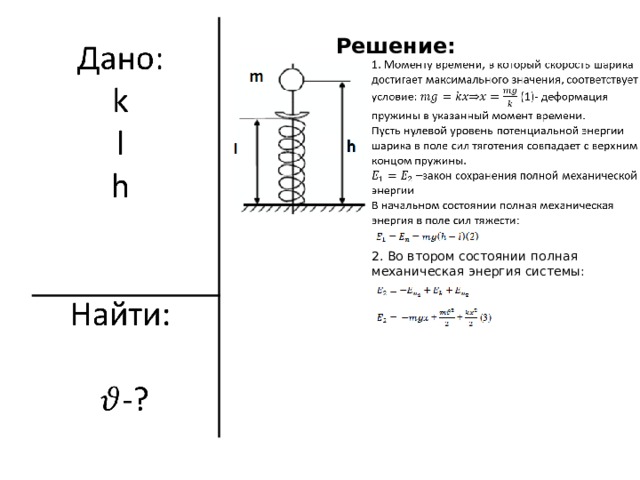
Решение:

2. Во втором состоянии полная механическая энергия системы:

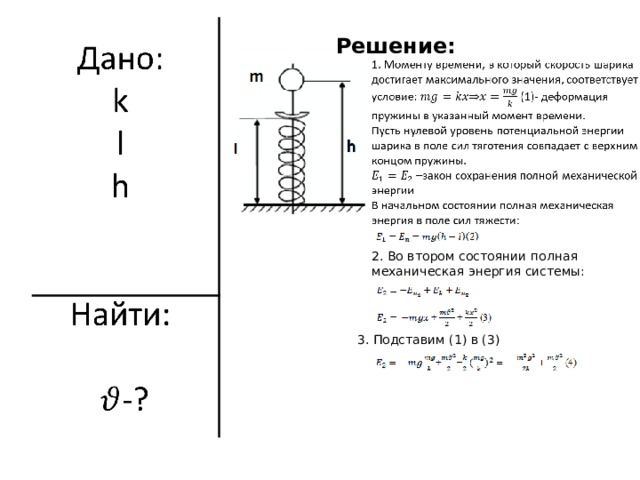
Решение:

2. Во втором состоянии полная механическая энергия системы:

3 . Подставим (1) в (3)

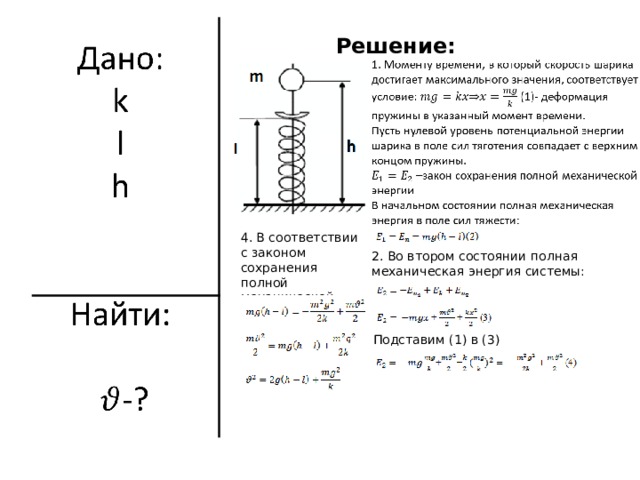
Решение:

4 . В соответствии с законом сохранения полной механической энергии:

2. Во втором состоянии полная механическая энергия системы:

3 . Подставим (1) в (3)

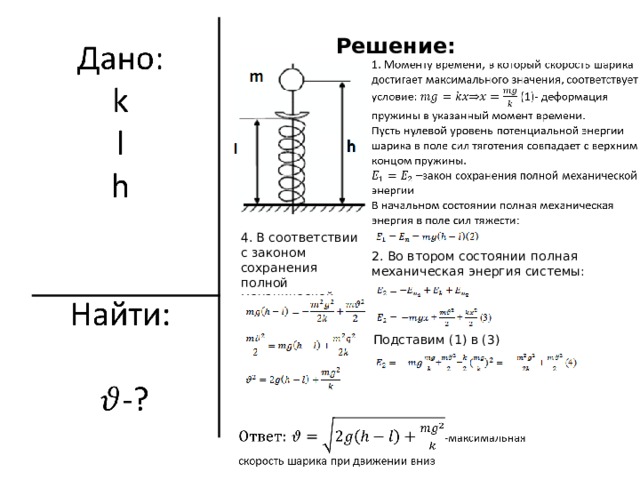
Решение:

4 . В соответствии с законом сохранения полной механической энергии:

2. Во втором состоянии полная механическая энергия системы:

3 . Подставим (1) в (3)

Задача 3

На гладкой горизонтальной поверхности движется «горка» высотой h и массой M . Основание горки плавно переходит в плоскость (см. рисунок). На пути «горки» лежит шайба массой m . При какой наименьшей скорости «горки» шайба перевалит через её вершину? Трение отсутствует.

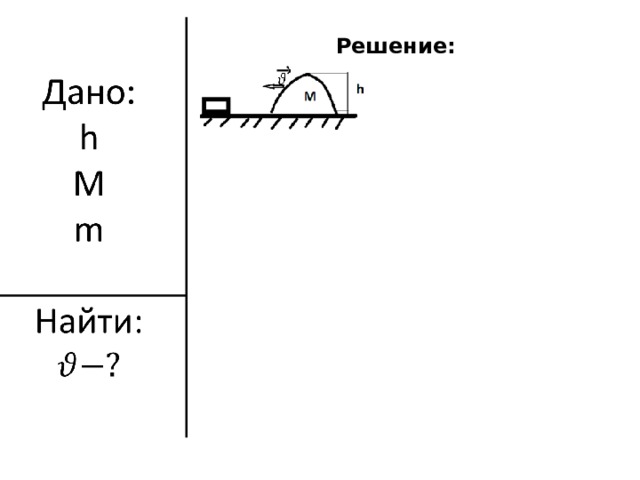
Решение:

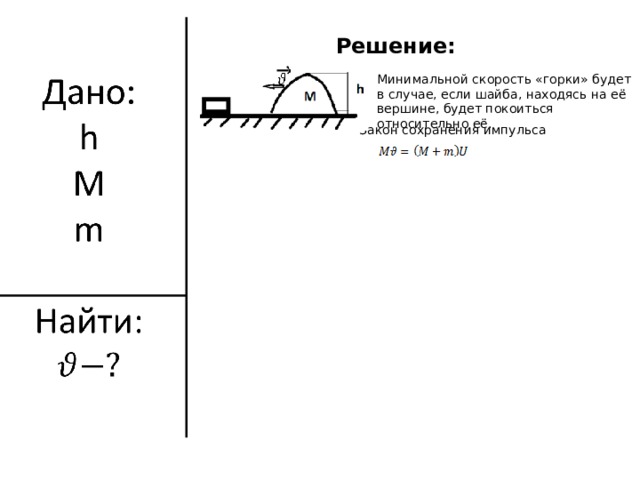
Решение:

Минимальной скорость «горки» будет в случае, если шайба, находясь на её вершине, будет покоиться относительно её.

Закон сохранения импульса

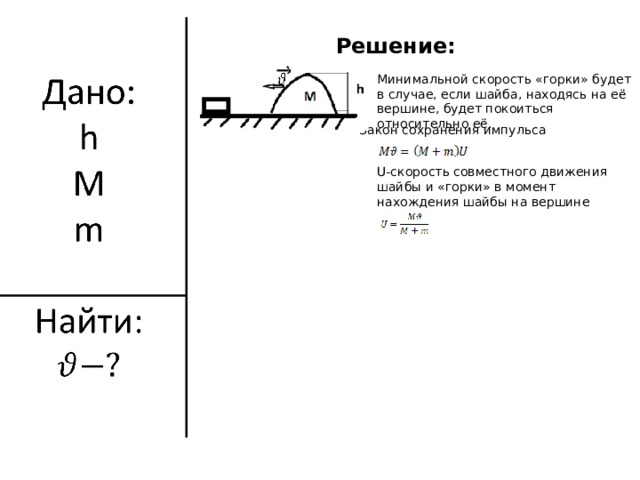
Решение:

Минимальной скорость «горки» будет в случае, если шайба, находясь на её вершине, будет покоиться относительно её.

Закон сохранения импульса

U -скорость совместного движения шайбы и «горки» в момент нахождения шайбы на вершине «горки»

Решение:

Минимальной скорость «горки» будет в случае, если шайба, находясь на её вершине, будет покоиться относительно её.

Закон сохранения импульса

U -скорость совместного движения шайбы и «горки» в момент нахождения шайбы на вершине «горки»

Закон сохранения полной механической энергии

В начальном состоянии:

В конечном состоянии:

Решение:

Минимальной скорость «горки» будет в случае, если шайба, находясь на её вершине, будет покоиться относительно её.

Закон сохранения импульса

U -скорость совместного движения шайбы и «горки» в момент нахождения шайбы на вершине «горки»

Закон сохранения полной механической энергии

В начальном состоянии:

В конечном состоянии:

Подставим (1) в (4)

Решение:

Минимальной скорость «горки» будет в случае, если шайба, находясь на её вершине, будет покоиться относительно её.

Закон сохранения импульса

Подставим (3) и (5) в (2)

U -скорость совместного движения шайбы и «горки» в момент нахождения шайбы на вершине «горки»

Закон сохранения полной механической энергии

В начальном состоянии:

-минимальная скорость «горки», при которой шайба перевалит через её вершину.

В конечном состоянии:

Подставим (1) в (4)

Задача 4

Во сколько раз уменьшится скорость атома гелия после центрального упругого столкновения с неподвижным атомом водорода?

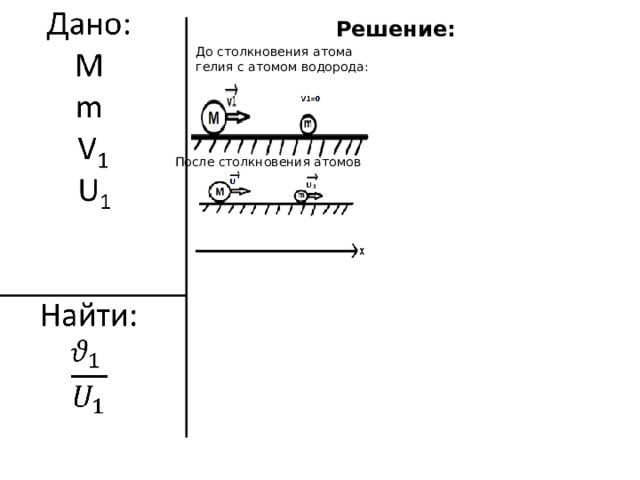
Решение:

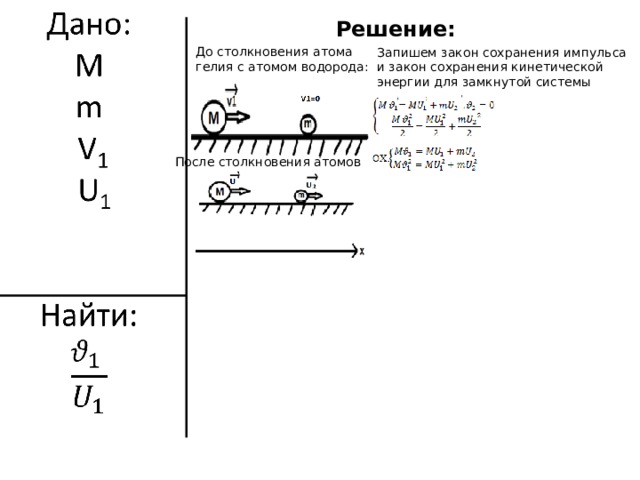
До столкновения атома гелия с атомом водорода:

После столкновения атомов

Решение:

До столкновения атома гелия с атомом водорода:

Запишем закон сохранения импульса и закон сохранения кинетической энергии для замкнутой системы

После столкновения атомов

Решение:

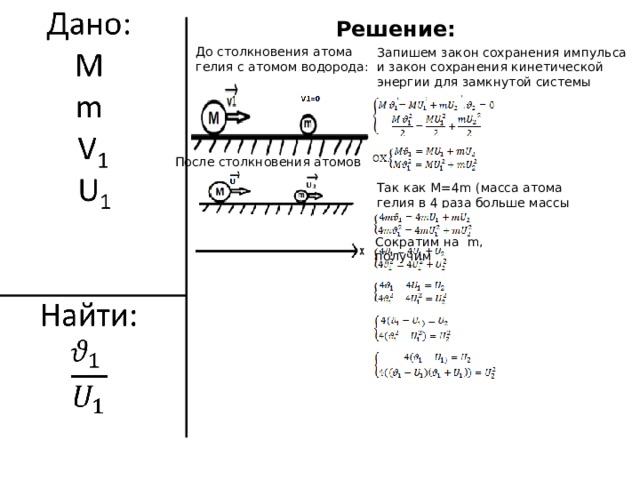
До столкновения атома гелия с атомом водорода:

Запишем закон сохранения импульса и закон сохранения кинетической энергии для замкнутой системы

После столкновения атомов

Так как M =4 m (масса атома гелия в 4 раза больше массы атома водорода)

Сократим на m , получим

Решение:

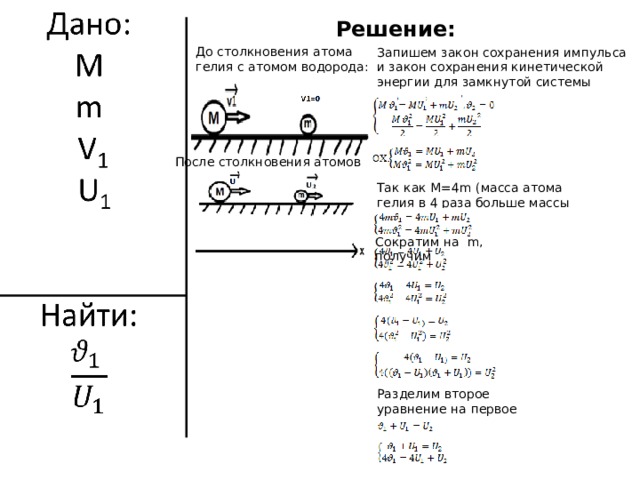
До столкновения атома гелия с атомом водорода:

Запишем закон сохранения импульса и закон сохранения кинетической энергии для замкнутой системы

После столкновения атомов

Так как M =4 m (масса атома гелия в 4 раза больше массы атома водорода)

Сократим на m , получим

Разделим второе уравнение на первое

Решение:

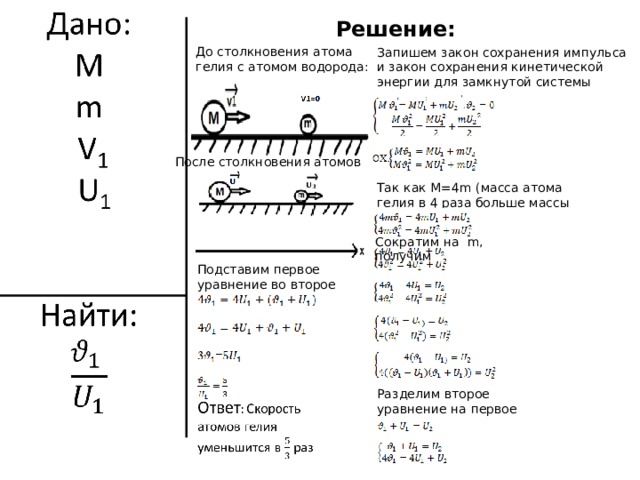
До столкновения атома гелия с атомом водорода:

Запишем закон сохранения импульса и закон сохранения кинетической энергии для замкнутой системы

После столкновения атомов

Так как M =4 m (масса атома гелия в 4 раза больше массы атома водорода)

Сократим на m , получим

Подставим первое уравнение во второе

Разделим второе уравнение на первое