Решение треугольников

Тема урока: «Решение треугольников» (9 класс)

Урок применения и совершенствования знаний.

Цель урока:

- познакомить учащихся с методами решения треугольников;

- совершенствовать алгоритм решения практических задач на нахождение длины стороны треугольника по двум другим;

- расширить способы построения и исследования математических моделей для решения прикладных задач; закрепить знание учащимися теорем синусов и косинусов;

- уметь решать комбинированные задачи с использованием 2-3 алгоритмов.

Оборудование: таблица «Брадиса», дидактический материал «Задачи на готовых чертежах 7-9 классы», микрокалькуляторы.

Универсальные учебные действия(УУД):

Регулятивные: учитывать правило в планировании и контроле способа решения.

Познавательные: ориентироваться на разнообразие способов решения задач.

Коммуникативные: учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве.

Ход урока.

1. Организация внимания. Проверка домашнего задания.

1. Решение задач №1027, №1032. (двое учащихся у доски объясняют решение задач).

2. Актуализация изученного материала. Решение задач по готовым чертежам.

Слайд 1.

По чертежам данным на слайдах презентации найти неизвестный элемент треугольника, расписывая

теоремы синусов и косинусов. После выполнения проверить по доске правильность своей записи и

оценить себя. Слайды в презентации переключаются по времени первые 3 задачи по 2 минуты,

последние 2 по 3 минуты.

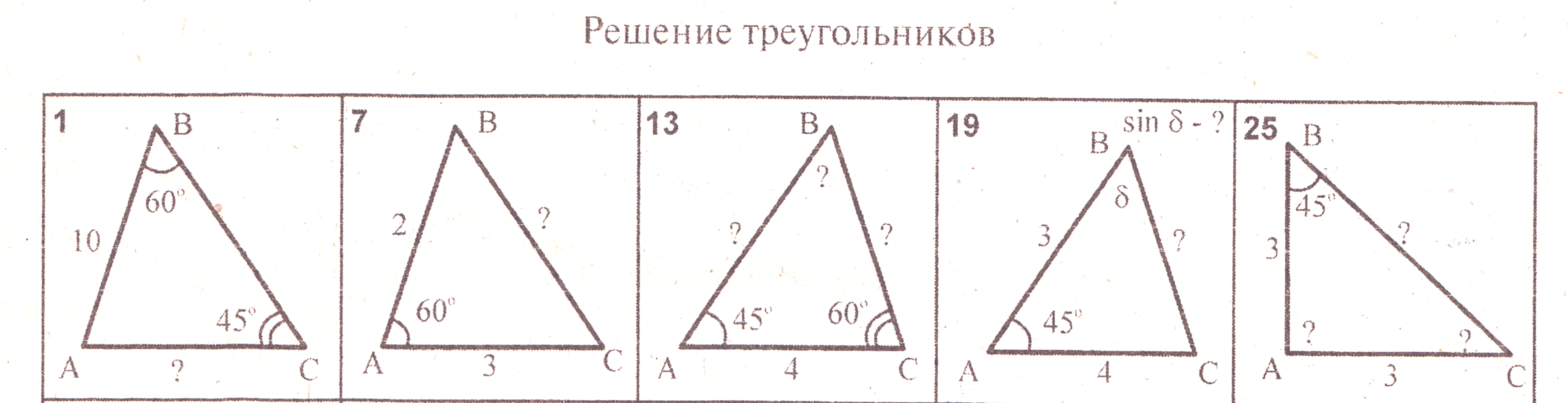
1. Мозговой штурм (устно).

Учитель задаёт вопросы:

• Теорема косинусов?

• Теорема синусов?

• Теорема о сумме углов треугольника?

• Формулы приведения острых и тупых углов для синуса и косинуса?

Отвечают на поставленные вопросы.

Ответы учеников:

• Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного

произведения этих сторон на косинус угла между ними.

• Стороны треугольника

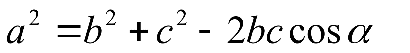
пропорциональны синусам противолежащих углов.

• Сумма углов треугольника равна 180 ̊ .

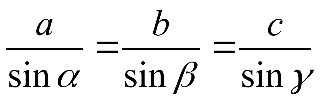
1. Актуализация изучения нового материала.

1. Сообщение темы и цели урока.

- Что означают слова «решение треугольника»?

(Решением треугольника называется нахождение всех его шести элементов (то есть трех сторон и трех углов) по каким-нибудь трем данным элементам, определяющим треугольник).

1. Объяснение способов решения задач на нахождение шести элементов треугольника.

При решении треугольников используют теоремы синусов и косинусов, причем при вычислении углов треугольника предпочтительнее использовать теорему косинусов, а не теорему синусов. Например, зная три стороны треугольника, для вычисления первого угла применяем теорему косинусов, а для вычисления второго угла можно использовать как ту, так и другую теоремы. Но поскольку синус угла равен синусу смежного с ним угла, то нахождение синуса угла еще не позволяет определить сам угол – он может быть острым или тупым. Если же вычислить косинус угла, то по его знаку и величине угол определяется однозначно.

3. Рассмотрим три задачи на решение треугольника:

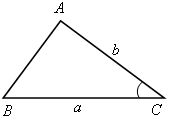
1) решение треугольника по двум сторонам и углу между ними;

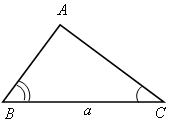
2) решение треугольника по стороне и прилежащим к ней углам;

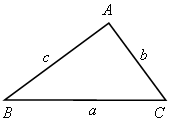
3) решение треугольника по трем сторонам.

При этом будем пользоваться следующими обозначениями для сторон треугольника АВС: АВ = с; ВС = а; СА = b.

4. В тетрадях учащиеся оформляют таблицу-памятку:

(Слайд 2)

1. Актуализация изученного материала.

1. Первичное усвоение изученного материала.

- Самостоятельно учащиеся разбирают решение примера по рисунку 294 на странице 255 учебника.

2. Решение задач.

№1025 (б,г,и) (работа в парах). Проверка выполнения заданий.

(Слайд 3)

1. Закрепление изученного материала.

1. Математический диктант (письменная индивидуальная работа)

(Слайд 4, 5)

По чертежу данному на презентации записать теорему синусов и косинусов и после

выполнения проверить по доске правильность своей записи и оценить себя.

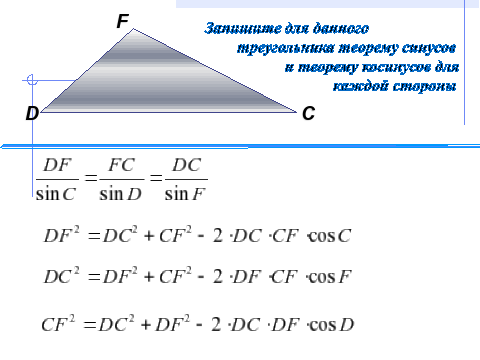
Пишут самостоятельно теоремы по данному чертежу. По окончании ученики сверяют

с ключом ответов учителя на интерактивной доске и выставляют себе баллы в листы оценивания.

1. Физминутка для глаз.

2. Мозговой штурм (устно).

Учитель задаёт вопросы. Типы задач:

• Решение треугольников по стороне и по двум углам.

• Решение треугольников по двум сторонам и углу между ними.

• Решение треугольников по трём сторонам.

• Решение треугольников по двум сторонам и углу, лежащему напротив одной из них.

Отвечают на поставленные вопросы.

Ответы учеников:

• Применим теорему о сумме углов треугольника и теорему синусов.

• Применим теорему о сумме углов треугольника и теорему косинусов.

• Применим теорему о сумме углов треугольника и теорему косинусов.

• Применим теорему о сумме углов треугольника и теорему синусов.

1. Итог урока. Домашнее задание.

1. Написать творческую работу о «Треугольнике». № 1025а,д,е,з, 1028.

2. Выбрать одну из 6 шляп мышления и попробовать дать рефлексию урока и своих знаний на конец урока.