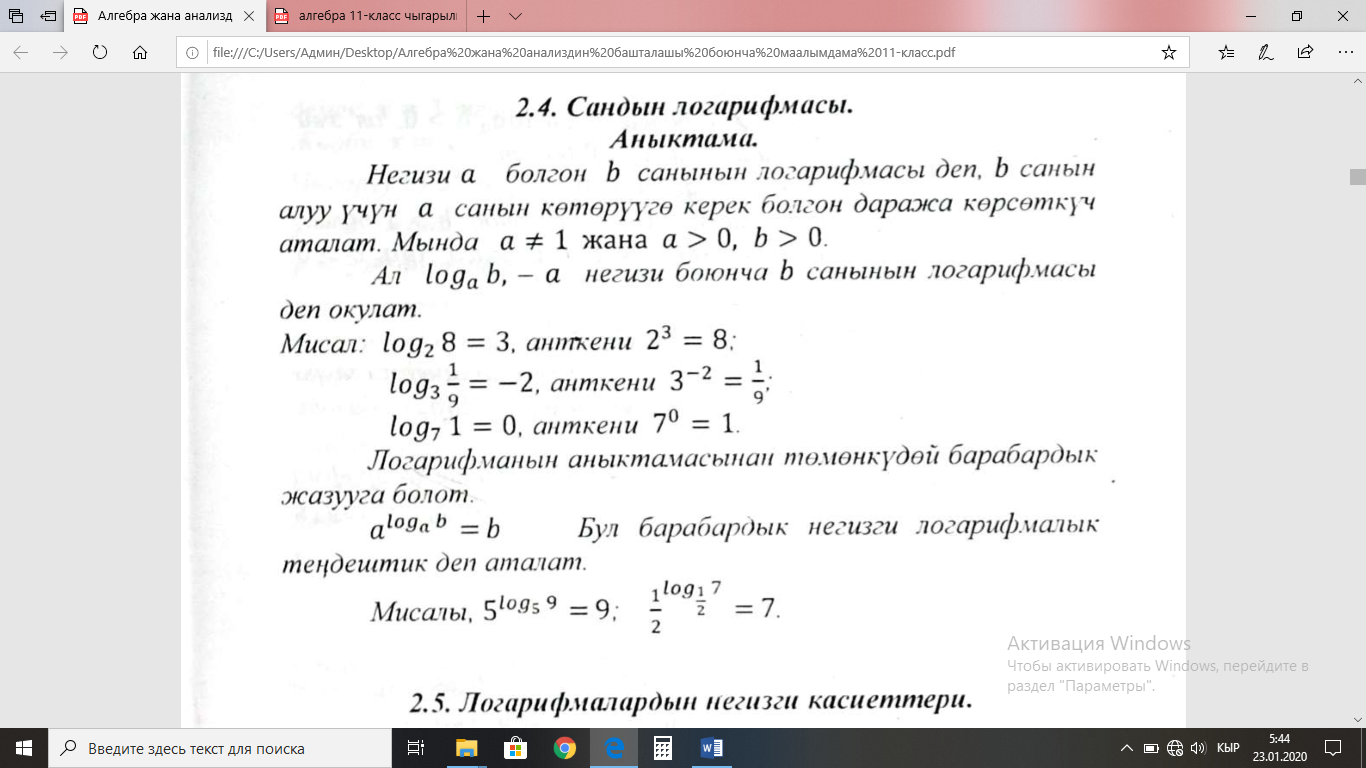
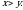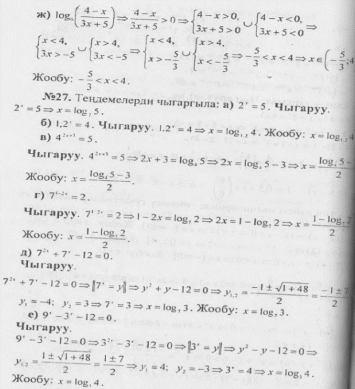|
11. А ТИЛКЕСИ Б ТИЛКЕСИ 
ABCD – квадрат
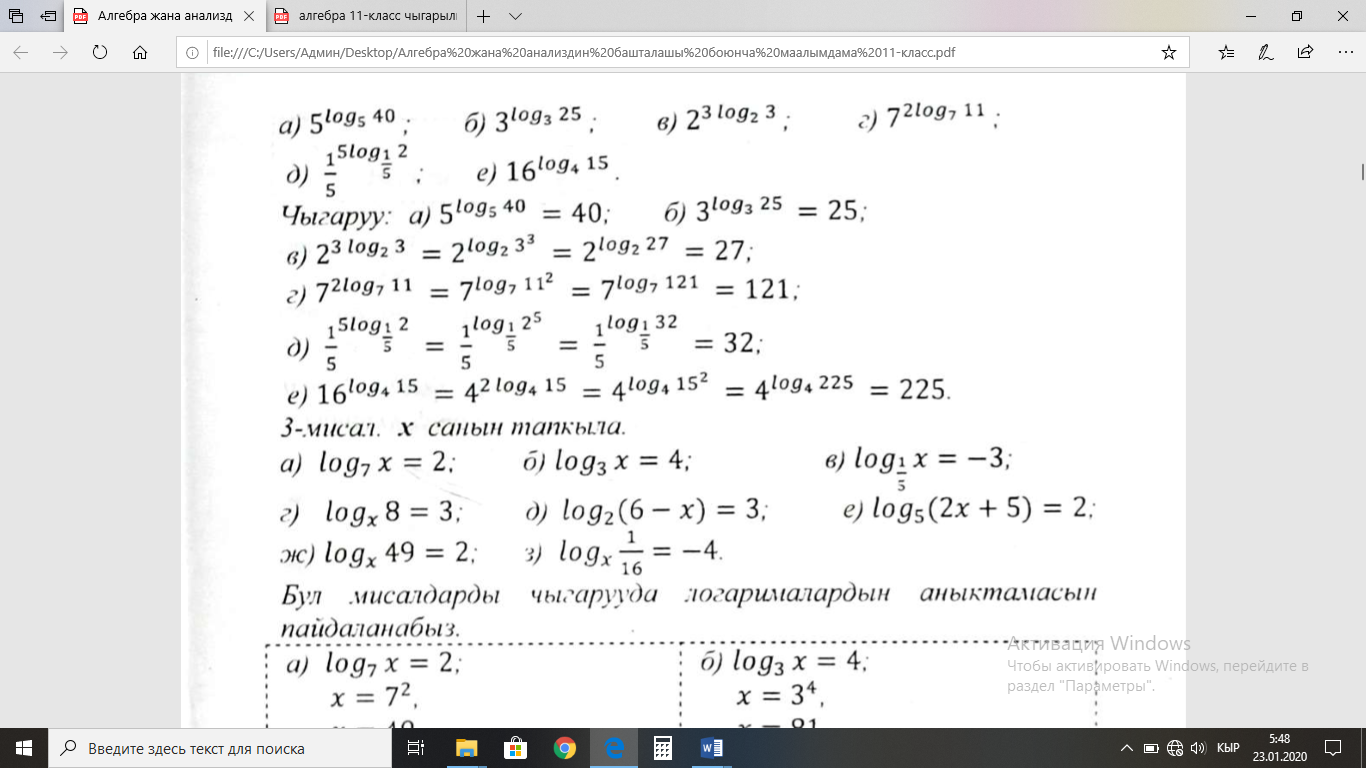
|
 кесиндисинин узундугу кесиндисинин узундугу
|
|
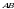 кесиндисинин узундугу кесиндисинин узундугу
|
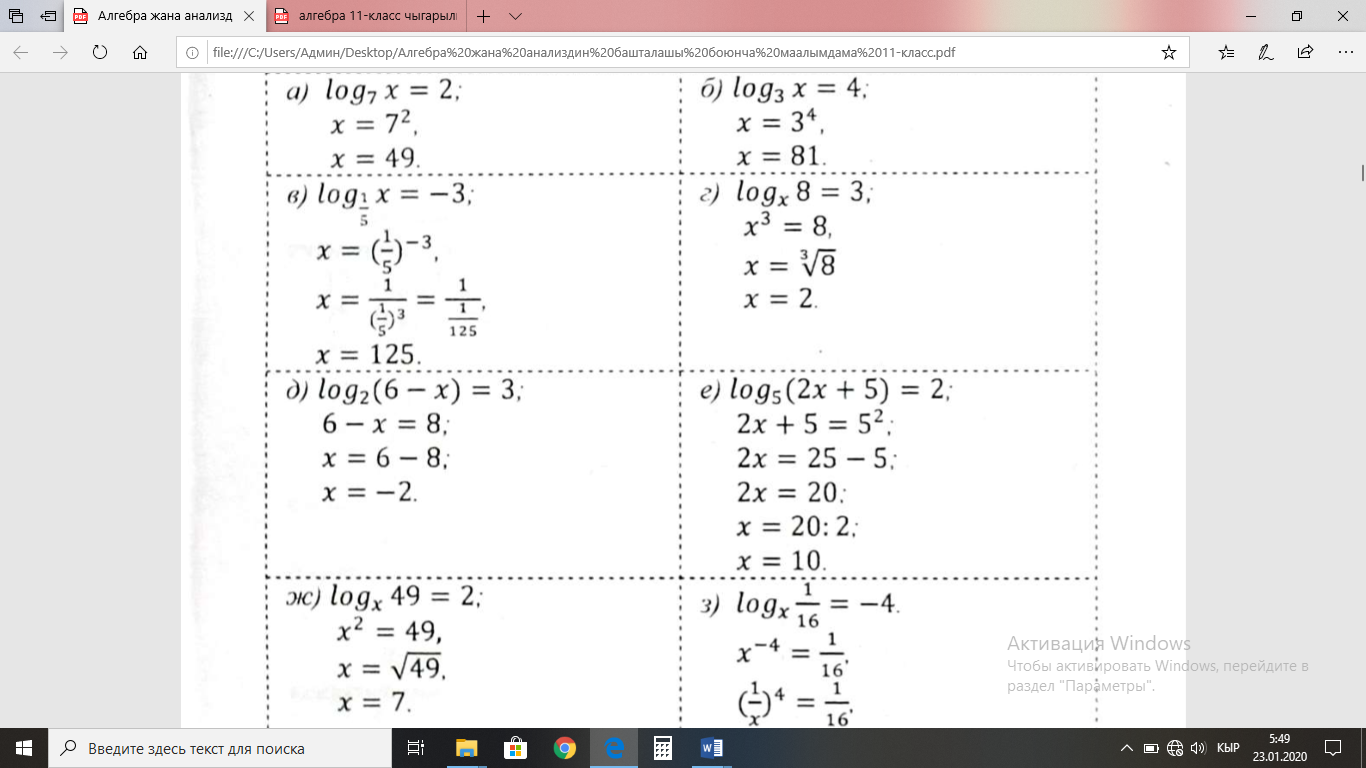
Чыгарылышы. 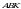 үч бурчтугунда үч бурчтугунда 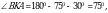 демек, бул үч бурчтук тең капталдуу, демек, бул үч бурчтук тең капталдуу,
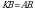 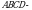 квадрат болгондуктан, квадрат болгондуктан, 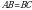 , демек, , демек, 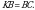
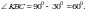
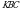 үч бурчтугунда үч бурчтугунда 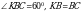 жана жана 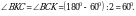
Андай болсо, бул үч бурчтук тең жактуу, демек, 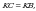 ал эми ал эми 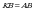 болгондуктан, болгондуктан, 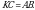 А ТИЛКЕСИНДЕГИ чоңдук Б ТИЛКЕСИНДЕГИ чоңдукка барабар. Туура жооп: В.
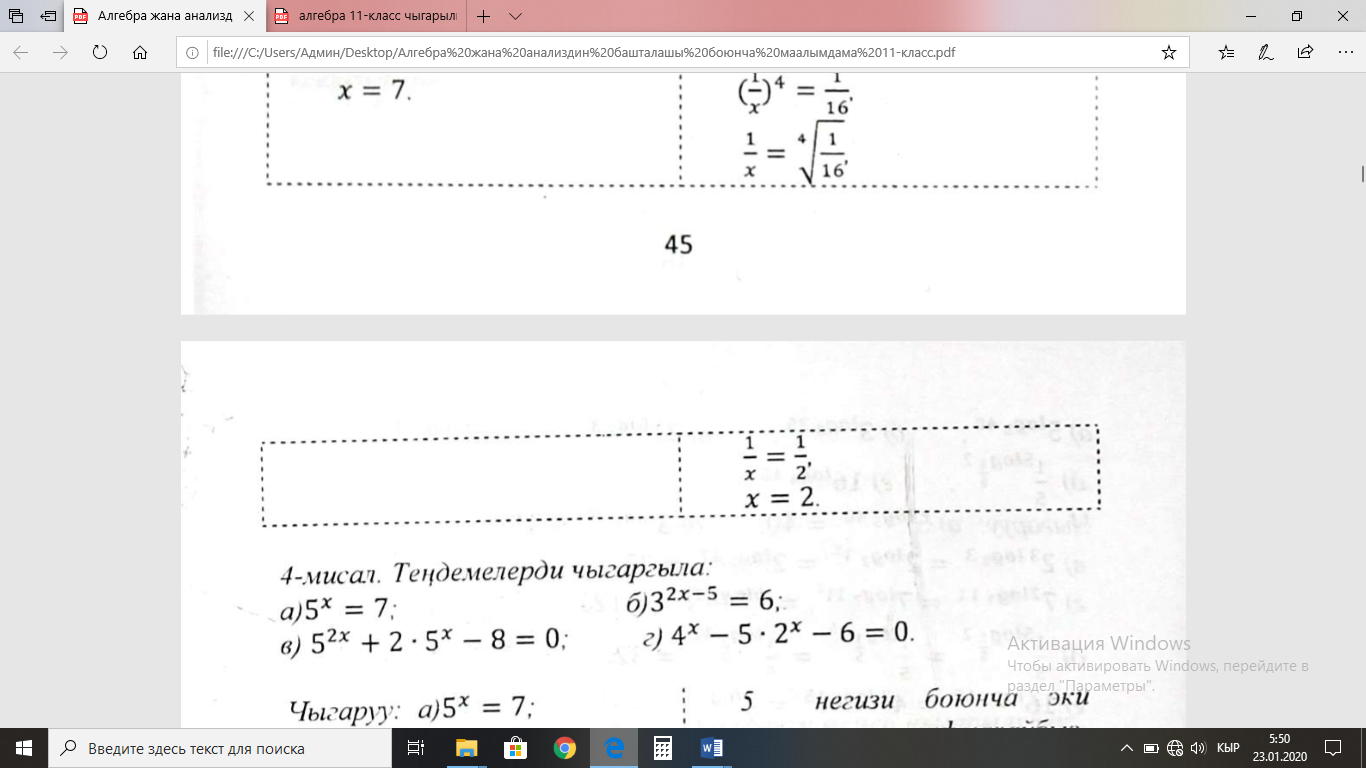
12. А ТИЛКЕСИ Б ТИЛКЕСИ
 санынын бүтүн бөлүгү болуп х-тен ашпаган эң чоң бүтүн сан аталат. санынын бүтүн бөлүгү болуп х-тен ашпаган эң чоң бүтүн сан аталат.  санынын бүтүн бөлүгү санынын бүтүн бөлүгү 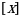 деп белгиленет. деп белгиленет.
Чыгарылышы. 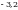 -ден ашпаган эң чоң бүтүн сан -ден ашпаган эң чоң бүтүн сан 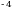 кө барабар, демек, кө барабар, демек, 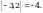
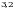 -ден ашпаган эң чоң бүтүн сан -ден ашпаган эң чоң бүтүн сан  кө барабар. кө барабар. 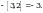
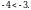
Б ТИЛКЕСИНДЕГИ сан А ТИЛКЕСИНДЕГИ сандан чоң Туура жооп: Б.
13. 1ден 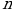 -ге чейинки удаалаш бүтүн оң сандардын, -ге чейинки удаалаш бүтүн оң сандардын, 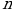 санын кошкондогу көбөйтүндүсү санын кошкондогу көбөйтүндүсү 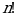 болуп белгиленет. болуп белгиленет. 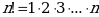 А ТИЛКЕСИ Б ТИЛКЕСИ
Чыгарылышы. Жогорудагы маалыматты пайдаланып, эсептеп чыгалы: 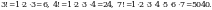 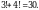
А ТИЛКЕСИНДЕГИ чоңдук Б ТИЛКЕСИНДЕГИ чоңдуктан чоң. Туура жооп: А.
14.
А ТИЛКЕСИ Б ТИЛКЕСИ
Кубдун көлөмү 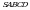 пирамидасынын пирамидасынын көлөмүнөн  эсе чоң. эсе чоң.
Чыгарылышы. 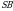 кубунун капталы кубунун капталы 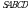 пирамидасынын бийиктиги болуп эсептелет. Ал эми пирамиданын көлөмү пирамидасынын бийиктиги болуп эсептелет. Ал эми пирамиданын көлөмү 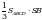 барабар болгондуктан, барабар болгондуктан, 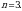
Туура жооп: В.
15.
А ТИЛКЕСИ Б ТИЛКЕСИ
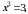 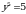
Чыгарылышы. 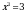 барабардыгынын эки бөлүгүн бешинчи даражага көтөрүп, натыйжада барабардыгынын эки бөлүгүн бешинчи даражага көтөрүп, натыйжада 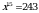 барабардыгын алабыз. барабардыгын алабыз.
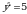 барабардыгынын эки бөлүгүн үчүнчү даражага көтөрүп, натыйжада барабардыгынын эки бөлүгүн үчүнчү даражага көтөрүп, натыйжада 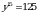 барабардыгын алабыз барабардыгын алабыз
Ошентип, 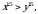 демек, демек, 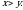 Б ТИЛКЕСИНДЕГИ чоңдук А ТИЛКЕСИНДЕГИ чоңдуктан чоң. Туура жооп: Б.
| 






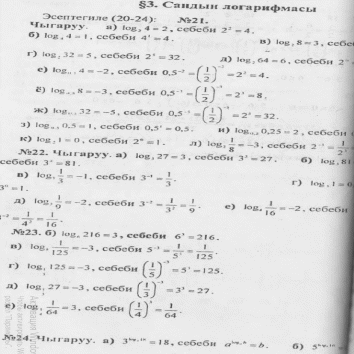

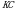 кесиндисинин узундугу
кесиндисинин узундугу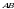 кесиндисинин узундугу
кесиндисинин узундугу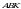 үч бурчтугунда
үч бурчтугунда 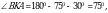 демек, бул үч бурчтук тең капталдуу,
демек, бул үч бурчтук тең капталдуу, 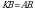
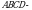 квадрат болгондуктан,
квадрат болгондуктан, 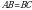 , демек,
, демек, 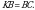
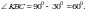
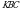 үч бурчтугунда
үч бурчтугунда 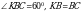 жана
жана 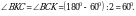
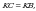 ал эми
ал эми 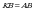 болгондуктан,
болгондуктан, 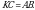
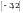
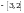
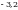 -ден ашпаган эң чоң бүтүн сан
-ден ашпаган эң чоң бүтүн сан 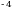 кө барабар, демек,
кө барабар, демек, 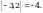
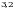 -ден ашпаган эң чоң бүтүн сан
-ден ашпаган эң чоң бүтүн сан  кө барабар.
кө барабар. 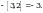
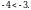
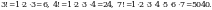
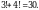
 пирамидасынын
пирамидасынын  эсе чоң.
эсе чоң. 

 кубунун капталы
кубунун капталы 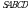 пирамидасынын бийиктиги болуп эсептелет. Ал эми пирамиданын көлөмү
пирамидасынын бийиктиги болуп эсептелет. Ал эми пирамиданын көлөмү 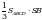 барабар болгондуктан,
барабар болгондуктан, 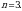
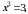
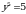
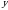

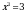 барабардыгынын эки бөлүгүн бешинчи даражага көтөрүп, натыйжада
барабардыгынын эки бөлүгүн бешинчи даражага көтөрүп, натыйжада 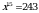 барабардыгын алабыз.
барабардыгын алабыз. 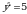 барабардыгынын эки бөлүгүн үчүнчү даражага көтөрүп, натыйжада
барабардыгынын эки бөлүгүн үчүнчү даражага көтөрүп, натыйжада 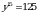 барабардыгын алабыз
барабардыгын алабыз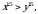 демек,
демек,