"Сфера и шар. Уравнение сферы"

Урок геометрии в 11-м классе по теме "Сфера и шар. Уравнение сферы"

Цель: ввести понятие сферы, шара и их элементов, вывести уравнение сферы в заданной прямоугольной системе координат, научить решать задачи по данной теме.

Кратчайший путь - путь по прямой?

Ход урока

1. Мотивация изучения темы

Сегодня мы затронем маленький кусочек этой геометрии и займемся изучением сферы и шара.

2. Объяснение новой темы

- Вспомните определение окружности (Окружность геометрическая фигура, состоящая из всех точек,расположенных на заданном расстоянии от данной точки).

- Дайте определение сферы (Сфера- поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки).

Сферой называют поверхность шара. У нее есть замечательное свойство: все ее точки находятся на одном и том же расстоянии от некоторой точки, находящейся внутри - центра сферы. Если разрезать сферу плоскостью, то получим окружность. Сфера единственная поверхность, при пересечении которой плоскостью всегда получается окружность. Если пересекающая плоскость проходит через центр сферы, то полученная окружность будет самой большой. Еще одно важное свойство: из всех сосудов одинаковой вместимости у сферического наименьшая поверхность.

Сегмент шара - это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента

Сектором называется часть шара, ограниченная совокупностью всех лучей, исходящих из центра шара О и образующих круг на его поверхности с радиусом r.

- По аналогии с окружностью,дайте определение радиуса сферы, центра и диаметра сферы. (Диаметр сферы -отрезок, соединяющий две точки сферы и проходящий через ее центр. (= 2R))

- Вспомните определение круга(Круг - часть плоскости, ограниченная окружностью).

- Дайте определение шара (Шар -тело, ограниченное сферой).

- Есть и другое определение шара(Шар радиуса R с центром в точке О называется тело, которое содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая О), и не содержит других точек).

- Сфера может быть получена вращением полуокружности вокруг ее диаметра, а шар - вращением полукруга вокруг его диаметра.

- Введем прямоугольную систему координат Oxyz и некоторую поверхность F . Уравнение с тремя переменными х, у,z называется уравнением поверхности Р, если этому уравнению удовлетворяют координаты любой поверхности F и не удовлетворяют координаты никакой точки, не лежащей на этой поверхности.

Поэтому уравнение сферы радиусаR с центром О (Х_о, У_о, Z_o) будет выглядеть таким образом: расстояние от произвольной точки М (х, у, z) до О (Х_о,У_о, Z_o) вычисляется по формуле

МО = 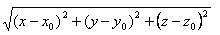,т.к. MO=R

R = , т .к. М ­ - любая точка сферы,то уравнение сферы

(х - х_о)²+ (у - у_о)² + (z - z_o)² == R²

Тогда уравнение шара (х -х_о)² + (у - у_о)² +(z - z_o)²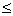 R ­

3. Формирование умений и навыков учащихся

№ 573 (проверка решения)

№ 576(а), № 578(а), № 577(а) самостоятельно.

4. Итог

- Дайте определение сферы; чем шар отличается от круга?

5. Домашнее задание

П. 58,59, № 573(б), 576(в), 579(б)