Дата проведения:.
Тема урока: синус и косинус двойного угла.
Тип урока: изучение нового материала.
Цели урока:
1)образовательные: формируют познавательную активность и мотивацию изучения математики; умения сравнивать, обобщать изучаемые факты; выделяют и формулируют познавательную цель, структурируют знания.
2)развивающие: развивать эмоции учащихся путем привлечения наглядности; развивать умение грамотно излагать свои мысли, обосновывать свои действия.
3)воспитательная: воспитать интерес к уроку
Литература: алгебра и начала математического анализа А.Н.Колмогоров
Ход урока
1)Организационный момент (1 мин.)
2)Повторение (5 мин.)
а) Ребус (2мин
) 
3) Новая тема
Теперь запишем все формулы двойного угла в виде списка.
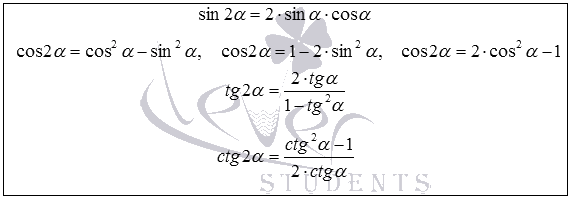
Заметим, что формулы синуса и косинуса двойного угла справедливы для любого угла 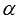 . Формула тангенса двойного угла имеет место для любых
. Формула тангенса двойного угла имеет место для любых 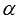 , при которых определен
, при которых определен 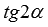 (то есть, при
(то есть, при 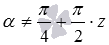 , где z – любое целое число). В свою очередь формула котангенса двойного угла справедлива для любых
, где z – любое целое число). В свою очередь формула котангенса двойного угла справедлива для любых 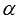 , при которых имеет место
, при которых имеет место 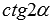 (то есть, при
(то есть, при 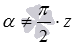 ).
).
Формулы двойного угла доказываются достаточно просто – они следуют из формул сложения.
4.Закрепление
Задание №1 Дано: сosα = -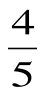 , π .
, π .
Вычислить: sin 2 α.
Решение.
-
sin 2α =2 sin α cosα; π , 3 четверть, sinα sin2 α + cos2 α = 1 следует, что sin2 α = 1- cos2 α,
sin α =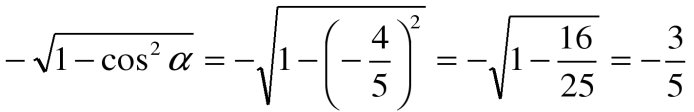 , sin α = -
, sin α = - 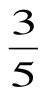 .
.
sin 2α =2 sin α cosα = 2.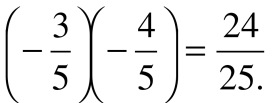 Sin 2α=
Sin 2α=  .
.
Ответ: sin 2α=  .
.
Задание№2 Дано: sin α = - 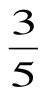 .
.
Вычислите: сos 2α.
Решение.
cos 2α = cos2 α – sin2 α, из основного тригонометрического тождества sin2 α + cos2 α = 1 следует, что
cos2 α = 1-sin2 α = 1 - 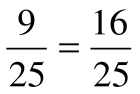 .
.
cos 2α = cos2 α – sin2 α =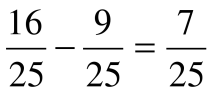
cos 2α =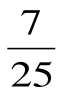 . Ответ: cos 2α =
. Ответ: cos 2α =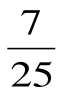 .
.
Задание№3 2) cos2 150 – sin2 150 = cos 2. 150 = cos 300= 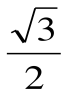 .
.
4) (cos 150 + sin 150)2 = cos2 150 +2 sin 150 cos150 + sin2 150=
= 1 + 2 sin 150 cos150 =1 + sin 300=1 + 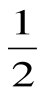 =
= 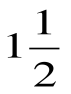 .
.
.
Вариант 1.
а) 2sin π/8 cos π/8; Вычислите cos 2α, sin 2α, если sin α = 0,6, Ответы: 1 вариант:1) а) ; б) 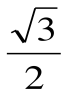 .
.
Вариант 2.
-
Вычислите:
а) 2sin π/12 cos π/12; Вычислите sin 2α, cos 2α, если cos α = 0,8 и 3π/2 π.
-
Ответы: 2 вариант: 1) а) ; б) 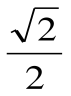 .
.
5.Итог урока
Вопросы по теме урока. Оценивание. д/задание







 . Формула тангенса двойного угла имеет место для любых
. Формула тангенса двойного угла имеет место для любых  (то есть, при
(то есть, при  , где z – любое ). В свою очередь формула котангенса двойного угла справедлива для любых
, где z – любое ). В свою очередь формула котангенса двойного угла справедлива для любых  (то есть, при
(то есть, при  ).
).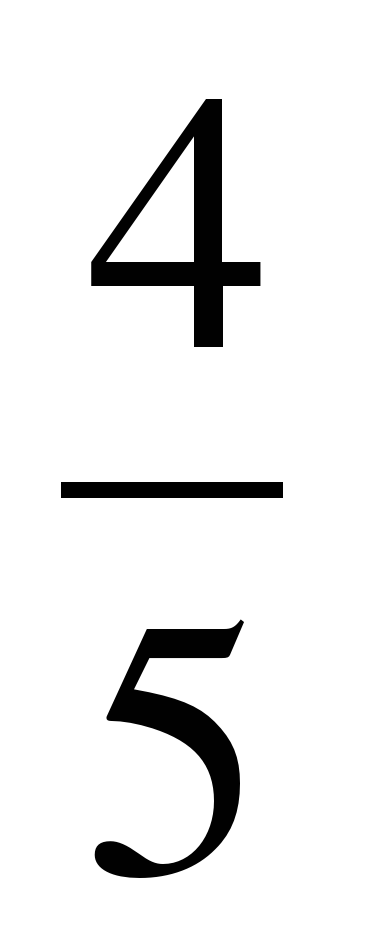 , π .
, π .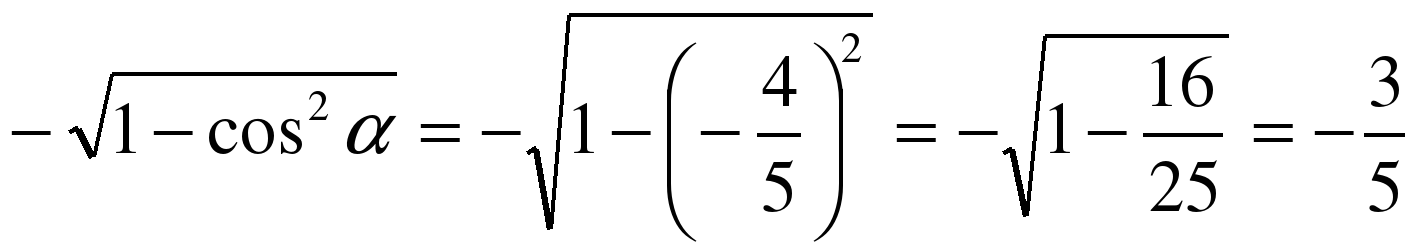 , sin α = -
, sin α = - 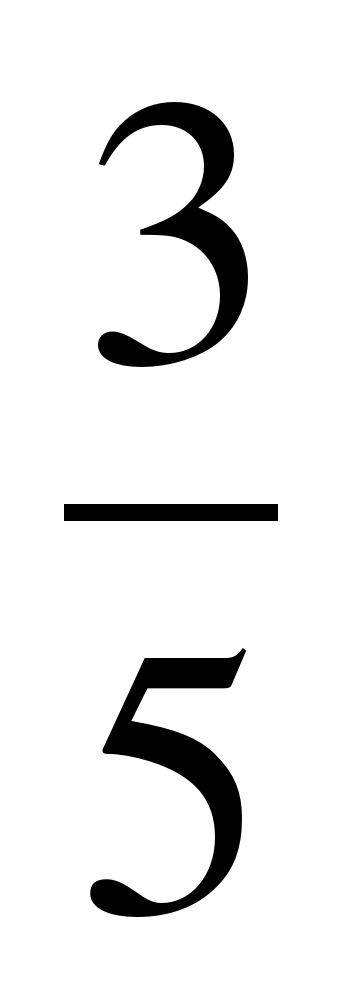 .
.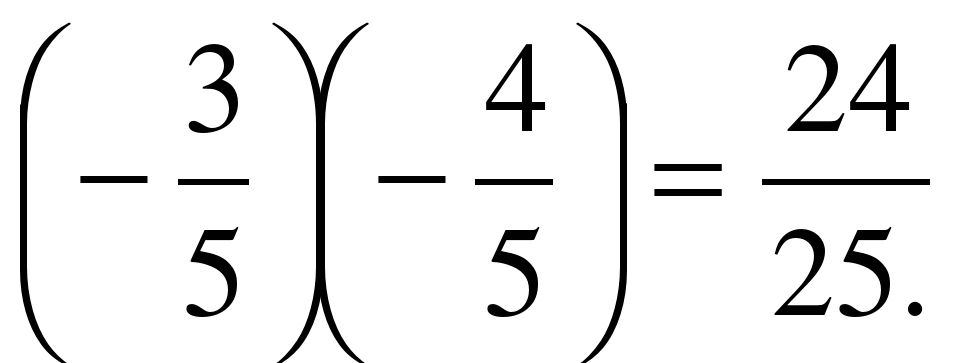 Sin 2α=
Sin 2α= 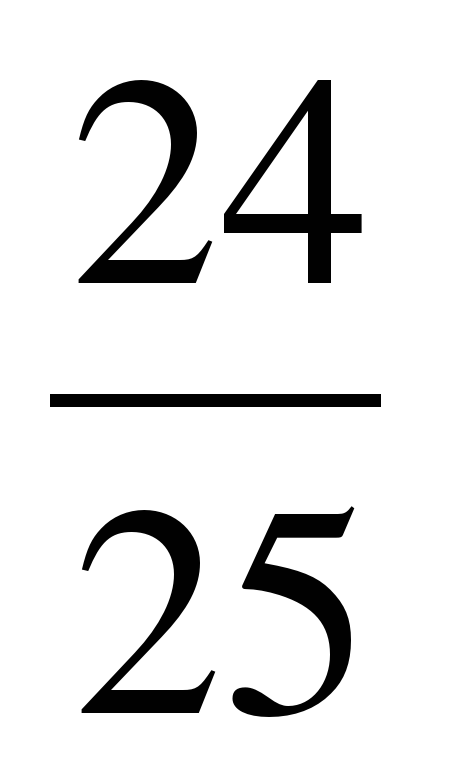 .
.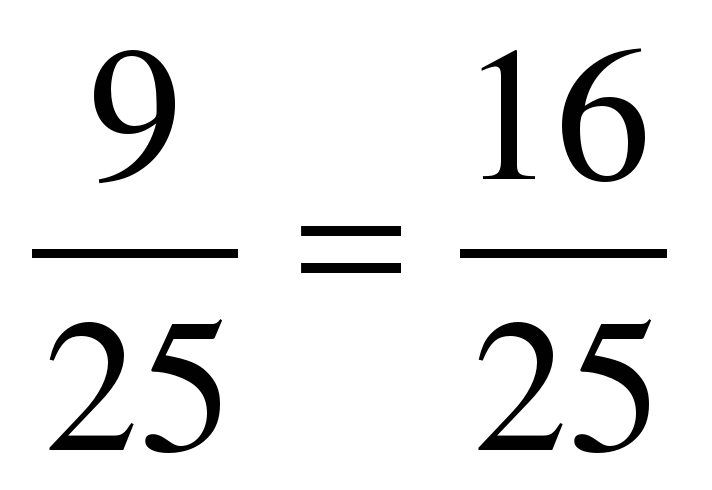 .
.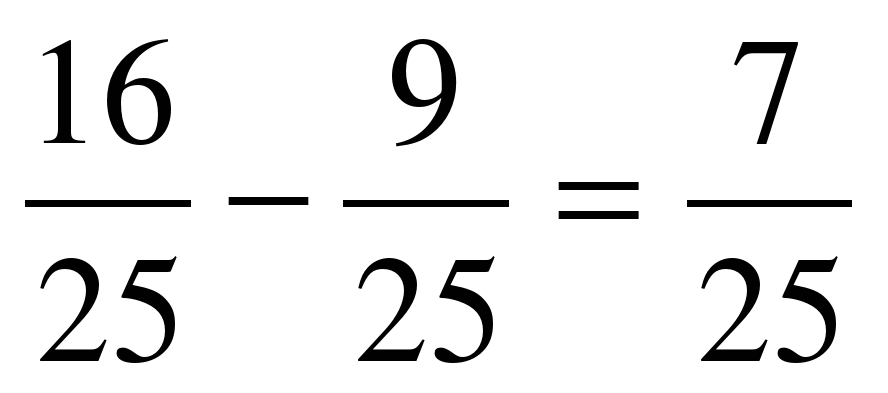
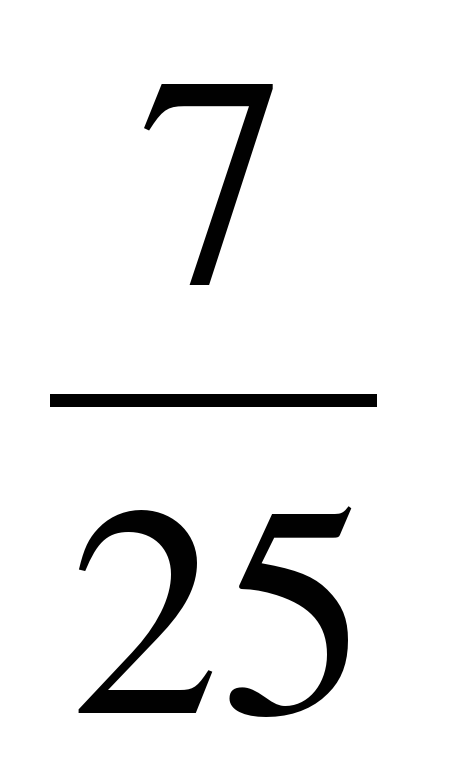 . Ответ: cos 2α =
. Ответ: cos 2α =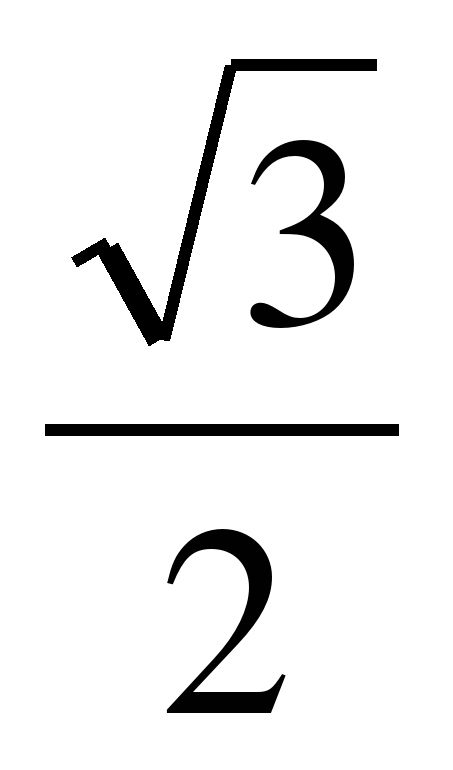 .
.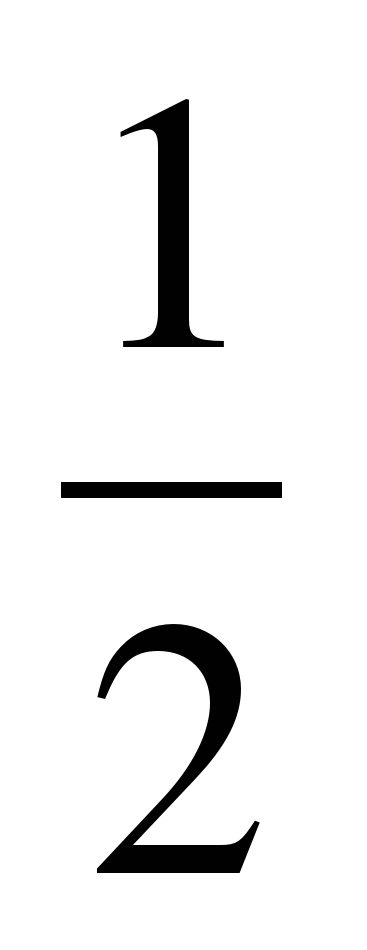 =
=  .
.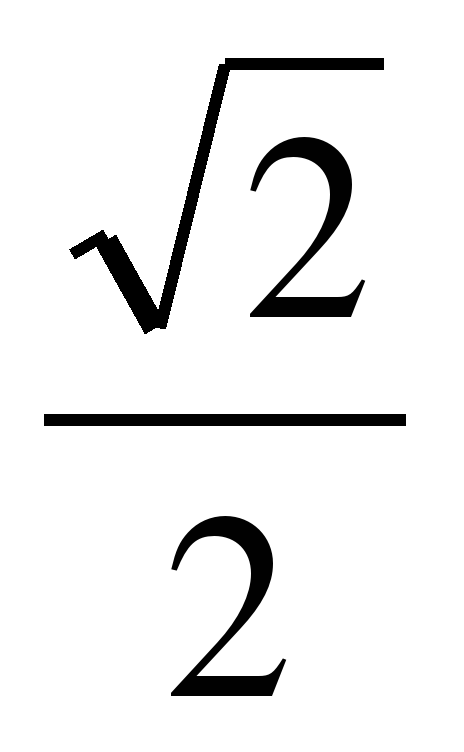 .
.