Тема урока: «Сложные задачи на движение по реке»
Учитель: Печикина Диана Игоревна
Класс: 5
Цели и задачи урока: сформировать навык решения задач на движение по реке (в среде, имеющей собственную скорость).
Предметные результаты: знать понятия: собственная скорость катера, скорость течения реки, уметь находить скорость катера по течению и против течения, перевод единиц времени и скорости.
Метапредметные и личностные результаты: воспитывать познавательный интерес к предмету, уметь выбирать наиболее эффективные способы решения поставленных задач.
Тип урока: урок формирования знаний, умений и навыков.
Методы и формы: устный опрос, проблемный метод изложения материала, применение ИКТ
Литература:
Математика. 5 класс: учебник для общеобразоват. учреждений / С. М. Никольский, М. К. Потапов, Н. Н. Решетников, А. В. Шевкин. —М.: Просвещение, 2012;
Математика. Дидактические материалы. 5 класс / М. К. Потапов, А. В. Шевкин.— М.: Просвещение, 2007–2012;
Печикина Д.И. «Использование современных информационных технологий при обучении поиску решения текстовых алгебраических задач» – Системы управления, технические системы: устойчивость, стабилизация, пути и методы исследования Материалы молодежной секции в рамках IV Международной научно-практической конференции. Елец, 2018. С. 273-277.
Печикина Д.И. «О различных способах решения текстовых задач» – Вестник Елецкого государственного университета им. И.А. Бунина Сер. «Педагогика» (История и теория математического образования)" Елец, 2017. С. 112-116.
Печикина Д.И. «Реализация метода математического моделирования при обучении математике» – Школа молодых учёных по проблемам естественных наук Сборник материалов областного профильного семинара. 2018. С. 27-31.
Оборудование и используемые учебные пособия:
Учебник
Карточки
Компьютер
Интерактивная доска
Ход урока
I. Организационный момент.
Создание психологической готовности участников: – Здравствуйте, проверьте свою готовность к уроку, на столе у вас должны быть: учебник, тетрадка, опорный конспект, пенал, дневник.
II. Актуализация использования компьютерного моделирования на уроках математики
В современном мире постоянно происходят изменения, совершается процесс модернизации.
Термин «модернизация» в последние несколько лет приобрел ярко выраженное социально-философское и культурологическое содержание. Именно этим термином определяют некоторый «способ общественного процесса, который отличается целенаправленным, управляющим характером. Процесс модернизации коснулся и образовательной сферы нашей страны» [2].
Строгие правила построения моделей (в силу различия их природы и назначения) сформулировать не представляется возможным, однако человечество накопило богатый опыт моделирования различных объектов и процессов.
В XXI веке, который по праву называют веком информационных технологий, при создании разного рода моделей помогает внедрение новых информационных технологий, в том числе и в образовательный процесс. Не вызывает сомнения тот факт, что информационные технологии играют немаловажную роль не только в науке, технике, но и в жизни общества. Повсеместное внедрение комплекса мер, направленных на обеспечение полного и своевременного использования достоверной информации, обобщенных знаний во всех социально значимых видах человеческой деятельности называют процессом информатизации общества [5]. Современное информационное пространство является и источником, и проводником постоянных изменений во всех сферах жизни современного человека, а также влияет на личностные качества самого человека.
Моделирование – это метод познания, способствующий созданию и исследовании моделей[5]. Что же такое – модель? Каждый человек хотя бы раз в жизни занимался моделированием: осознанно или нет, но с раненого детства мы создаем модели на основе или с помощью объектов окружающего мира. Например, еще дошкольниками дети стоят из конструктора башни или другие постройки, тем самым создавая модель зданий, которые они видели, но в силу своего возраста делают это без математической точности, одна — это можно назвать моделью окружающей их действительности. В дальнейшем созданные нами модели будет более полно и достоверно отражают существенные особенности изучаемых нами объектов, явлений или процессов.
Стоит отметить, что модели помогают и в различных науках, без их создания нельзя представить проектировании или создании различных технических устройств, не имея правильно смоделированного чертежа, нет возможности создать даже простую деталь. В физике с помощью моделирования изучаются практически все процессы взаимодействия и изменения объектов. Создание моделей не обошло стороной и царицу всех наук – математику: не имея четкой теоретической модели, отражающей строение свойства или поведение реальных объектов (знание теории, гипотезы и т.п.), нет возможности доказать более сложную – практическую задачу.
В настоящее время по технологии моделирования и области применения выделяют такие:
Схема №1.

III. Устный счет; целеполагание и мотивация
Как вы думаете, какой будет тема нашего сегодняшнего урока?
Для этого нам необходимо отгадать шифровку.
На слайде представлены несколько примеров, ваша задача устно найти их значения и в результате составить слово, которое подскажет нам тему сегодняшнего урока.

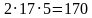
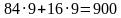
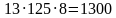
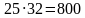
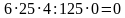
800 – а;
1300 – и;
58 –а;
170 –д;
900 – ч;
0 — з .
0 — з
58 –а;
170 –д
800 – а;
900 – ч
1300 – и;
Расположите числа в порядке возрастания. У нас получилось слово «Задачи». А какие мы будем решать задачи? Давайте отгадаем несколько загадок:
1) На море, в реках и озерах
Я плаваю, проворный и скорый.
Среди военных кораблей
Известен легкостью своей. (Катер)
2) Моряком ты можешь стать,
Чтоб границу охранять
И служить не на земле,
А на военном... (Корабль)
3) Ни корабль, ни лодка,
Ни вёсел, ни паруса,
А плывёт — не тонет. (Плот)
4) Паровоз без колес!
Вот так чудо- паровоз!
Не с ума ли он сошел –
Прямо по морю пошел! (Пароход)
Догадались с каким видом задач мы сегодня будем работать? Молодцы, конечно, с задачами на движение по реке. Откройте свои тетради запишите тему нашего урока: Решение задач на движение по реке.
Перед тем как приступить к решению давайте сформулируем цель и задачи нашего урока?
Формулируют задачи урока:
— повторить, что такое скорость и как она находится;
— как найти скорость по течению и скорость против течения;
— повторить, что такое время, и как оно находится;
— повторить, что такое расстояние, и как оно находится;
— решать задачи разными способами;
— составлять задачи.
Мы уже решали задачи по теме «Движение». Сегодня на уроке мы повторим и закрепим те знания, которые приобрели по этой теме, но для начала давайте немного вспомним:
Какие три величины характеризуют движение (На слайде формула).
Какие две ситуации чаще всего встречаются при движении по реке.
1) На интерактивной доске «разбросаны» части формул, ученик должен составить верные формулы:
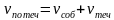
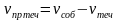
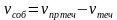

2) Давайте с вами заполним пропуске в таблице и повторим формулы для нахождения скорости. На ваших партах лежат листочки, в которых каждый из вас должен заполнить пропуски:
|
| 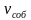
| 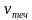
| 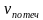
| 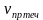
|
| 12 км/ч | 4 км/ч | 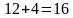 км/ч км/ч
| 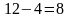 км/ч км/ч
|
| 25 км/ч | 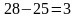 км/ч км/ч
| 28 км/ч |  км/ч км/ч
|
| 24 км/ч | 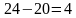 км/ч км/ч
|  км/ч км/ч
| 20 км/ч |
IV. Принцип применения компьютерного моделирования
Этапы создания математической модели выделяют исследователи данной проблемы [5]:
1) формализации – переход от практической задачи к построению математической модели и формулировке на её основе абстрактной математической задачи;
2) проведение математического исследования (решения задачи путем преобразования модели) – в ходе исследования модели получают некоторые теоретических сведений, т.е. результат;
3) истолкование полученного результата, при решение математической задачи исследуется его соответствия с исходной ситуацией, истолковывается в терминах описанная ситуация и применяется к ней;
4) преобразование модели, в более совершенную, этот этап основывается на связи анализированных данных об изучаемом объекте [5].
Для исследования конкретных моделей и построения новых в математике разработаны специальные методы, например, всеми известные: метод исследования элементарных функций, решения уравнений, доказательства утверждений, построения геометрических фигур и т.д. в результате возникновения данных моделей появлялись и особые методики использования на практике данных математических моделей, например, приёмы решения задач с помощью уравнений и систем уравнений, изучение различных явлений и процессов с помощью исследования соответствующих функций, геометрических фигур и т.д.
V. Усвоение новых знаний и способов действий.
Рассмотрим задачи на движение по реке, при решении которых удобно весь путь принимать за единицу (S=1), а скорость катера по течению реки (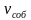 ), против течения (
), против течения (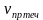 ) и скорость течения реки (
) и скорость течения реки (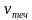 ) выражать как часть пути, пройденного за единицу времени.
) выражать как часть пути, пройденного за единицу времени.
Задание №1.
Расстояние между пристанями А и В на реке плот проплывает за 12 ч. Такое же расстояние теплоход проплывает по озеру за 4 ч. За сколько часов теплоход проплывёт расстояние между пристанями А и В:
а) по течению реки; б) против течения реки?
Решение.
|
| S | v | t |
| По течению | 1 | ? | 4 |
| Против течения | 1 | ? |
| ПЛОТ | 1 | 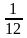
| 12 |
Пусть расстояние между пристанями А и В равно 1. Тогда
 (пути) — собственная скорость теплохода;
(пути) — собственная скорость теплохода;
 (пути) — скорость течения реки;
(пути) — скорость течения реки;
 (пути) — скорость теплохода по течению реки;
(пути) — скорость теплохода по течению реки;
 (пути) — скорость теплохода против течения реки;
(пути) — скорость теплохода против течения реки;
 (ч) – время движения теплохода по течению реки;
(ч) – время движения теплохода по течению реки;
 (ч) – время движения теплохода против течения реки;
(ч) – время движения теплохода против течения реки;
Ответ: катер проплывает расстояние между пристанями А и В: а) по течению реки за 3 часа; б) против течения реки за 6 часов.
VI. Физкультминутка
Поднимает руки класс – это «раз».
Повернулась голова – это «два».
Руки вниз, вперед смотри – это «три».
Руки в стороны пошире развернули на «четыре»,
С силой их к плечам прижать – это «пять».
Всем ребятам надо сесть – это «шесть».
VII. Закрепление
На интерактивной доске записано задание. В ходе решение задачи ученики заполняют таблицу-принятия задачи – вписываю имеющиеся данные из задачи.
№ 1062
Расстояние между пристанями А и В на реке плот проплывает за 15 мин, а катер проплывает расстояние АВ против течения реки за 30 мин. За сколько минут катер проплывёт расстояние АВ: а) по озеру; б) по течению реки?
Решение:
Таблица
|
| S | v | t |
| По течению | 1 | ? | 15 |
| Против течения | 1 | ? | 30 |
1)  (пути) – скорость течения.
(пути) – скорость течения.
2)  (пути) – скорость против течения.
(пути) – скорость против течения.
3) (пути) – скорость катера по озеру.
4)  (минут) – по озеру.
(минут) – по озеру.
5) (пути) – скорость катера по течению.
6)  (минут) – по течению реки.
(минут) – по течению реки.
Ответ: катер проплывает расстояние АВ за 10 минут по озеру и за 6 минут по течению реки.
Одному ученику предлагается выполнить задание у доски самостоятельно не комментируя, остальные – в своих тетрадях выполняют это задание самостоятельно.
№ 1066. а) Теплоход от Киева до Херсона идёт трое суток, а от Херсона до Киева четверо суток (без остановок). Сколько времени будут плыть плоты от Киева до Херсона?
Решение.
|
| S | v | t |
| от Киева до Херсона | 1 | ? | 3 |
| от Херсона до Киева | 1 | ? | 4 |
1)  (пути) —проходит теплоход в сутки по течению реки;
(пути) —проходит теплоход в сутки по течению реки;
2)  (пути) —проходит теплоход в сутки против течения реки;
(пути) —проходит теплоход в сутки против течения реки;
3) (пути) — на столько больше теплоход проплывает в сутки по течению, чем против течения (на столько течение относит теплоход или плоты за двое суток);
(пути) — на столько больше теплоход проплывает в сутки по течению, чем против течения (на столько течение относит теплоход или плоты за двое суток);
4) (пути) —на столько течение за сутки относит плоты;
(пути) —на столько течение за сутки относит плоты;
5)  (дня) —время движения плотов от Киева до Херсона.
(дня) —время движения плотов от Киева до Херсона.
VIII. Подведение итогов урока. Рефлексия.
— Ребята, подумайте, что во время урока у вас получалось хорошо, а что не очень? Сделайте для себя выводы. Ученики оценивают свою работу.
Сегодня на уроке я познакомился с…
Было интересно…
Было трудно…
Я научился…
Я затрудняюсь…
Меня удивило…
Мне захотелось…
Хотелось бы…
Как вы считаете, мы выполнили задачи, поставленные вначале урока?
С каким настроением вы работали на уроке? Изобразите карандашом своё настроение в виде смайлика.
IX. Домашнее задание.
№ 1063, 1066 (б), *Составить свою задачу на движение.
Стоит отметить, что наиболее сложным и часто вызывает затруднения – первый этап, так как он связан с выявлением зависимостей между искомыми и данными, а также данных между собой. Для облегчения процесса решения задачи и скорейшего нахождения пути решения от словесной модели ситуации, описанной в задаче, сначала переходят к вспомогательной (делают рисунки, строят схемы, составляют таблицы, краткую запись условия и т.п.), а уж затем – к математической модели, т.е. происходит процесс модернизации словесной задачи.
Говоря о моделировании, не следует забывать, что помимо всего прочего оно ещё является тем учебным действием и средством, без которого невозможно полноценное обучение[5].









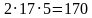
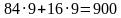
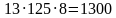
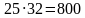
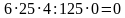
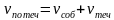
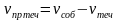
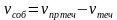

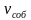
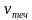
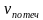
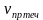
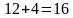 км/ч
км/ч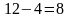 км/ч
км/ч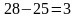 км/ч
км/ч км/ч
км/ч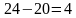 км/ч
км/ч км/ч
км/ч