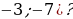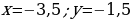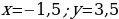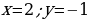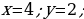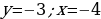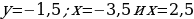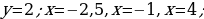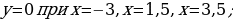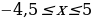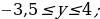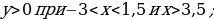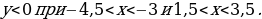Урок «График функции» (7 класс, учебник А.Г Мерзляк, В.Б. Полонский, М.С. Якир)
| Организационная структура урока |
| Этап урока | Содержание деятельности учителя | Содержание деятельности обучающегося
(осуществляемые действия) | Формируемые способы
деятельности |
| I. Организационный момент | Приветствие. Проверка готовности обучающихся к уроку. Создание в классе атмосферы психологического комфорта. – Рада вас приветствовать на уроке алгебры! – Сегодня мне нужна будет ваша помощь! Готовы сотрудничать? | Настраиваются на учебную деятельность. Концентрируют внимание на работе на уроке.
| Формирование навыков самоорганизации |
| II. Проверка домашнего задания | Организует самопроверку домашнего задания.
Задание № 812. Функция задана формулой 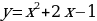 . При каких значениях х значение функции равно удвоенному значению аргумента? . При каких значениях х значение функции равно удвоенному значению аргумента? | Заполняют таблицу. | Задания | Решил правильно /
неправильно | Не смог решить потому, что … | |
|
|
| |
|
|
| Решение. 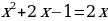
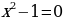
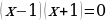
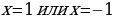
| Умение оценивать свои достижения |
| III. Актуализация опорных знаний и жизненного опыта. Постановка учебной задачи | Предлагает учащимся рассказать, что им известно о понятии «график функции».
Вопрос запуска постановки учебной задачи: – Достаточно ли у вас знаний о понятии «график функции»? Формулирует учебную задачу: – Исследовать график функции | Выступают перед классом или в группах. – О понятии «график функции» мне известно… – Нам рассказывал учитель… – Я находил информацию… – Я когда проводил исследования узнал… Осознают важность решения поставленной учебной задачи | Умение развивать навыки целеполагания |
| IV. Сообщение темы. Постановка цели и задач урока | Сообщает тему урока. Организует совместное с учащимися формулирование цели и задач урока. – Внимательно прочитайте тему урока. – Что от вас ожидается на уроке? – Какие цели и задачи вы можете перед собой поставить? | Записывают в тетрадь тему урока. Участвуют в формулировании целей и задач урока: – усвоить суть понятия «график функции»; – научиться анализировать графики функций | Умение принимать и сохранять учебную задачу |
| V. Мотивирование к учебной деятельности | Способствует обсуждению мотивационных вопросов: – Какие усилия нужно приложить, чтобы достичь поставленных целей и задач урока? – Насколько я осознаю важность изучения данной темы лично для себя? – Чувствую ли я ответственность за свою работу на уроке? – Какова моя цель на данный урок? | Отвечают на мотивационные вопросы. Создают условия для успешной учебной деятельности. | Умение выражать свои мысли. Развитие навыков самомотивации |
| VI. Создание ситуации затруднения. Работа над темой урока | Организует обсуждение проблемного вопроса: – Что нужно знать, чтобы построить график функции? Предлагает проанализировать определение понятия «график функции».
Объясняет учащимся, что если какая-то фигура является графиком функции f, то выполняются два условия: 1) если х0 – некоторое значение аргумента, а f(x0) – соответствующее значение функции, то точка с координатами (х0; f(x0)) обязательно принадлежит графику; 2) если (х0; у0) – координаты произвольной точки графика, то х0 и у0 – соответствующие значения независимой и зависимой переменных функции f, то есть у0 = f(x0). Организует обсуждение проблемного вопроса: – Можно ли утверждать, что любая фигура, изображенная на координатной плоскости, может служить графиком функции?
| Принимают участие в обсуждении проблемного вопроса. Испытывают определенные трудности при ответе на вопрос. Анализируют определение. Заполняют таблицу. | Определение | Ключевые слова | Вопросы учителю | | Графиком функции f называют геометрическую фигуру, состоящую из всех тех и только тех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции f | Геометрическая фигура, координатная плоскость, абсциссы, аргумент, ординаты | Почему…?
Что…? | Делают записи в рабочей тетради. Задают вопросы учителю.
Обсуждают проблемный вопрос. Предлагают свои идеи. Строят предположения. Выдвигают гипотезы. Проводят исследование. Выясняют, что фигура может являться графиком некоторой функции, если любая прямая, перпендикулярная оси абсцисс, имеет с этой фигурой не более одной общей точки | Умение выражать свои мысли в соответствии с задачей. Умение анализировать информацию.
Проводят исследование |
| VII. Закрепление изученного материала | Организует самоанализ усвоенных учащимися знаний. Оказывает помощь ученикам, которые не знают ответов на вопросы. Создает условия для дополнительного изучения вопросов, которые вызвали затруднения
| Отвечают на вопросы. Определяют свой уровень усвоения знаний. Заполняют таблицу. | Вопросы | Варианты ответов | | Знаю ответ на вопрос (+) | Не знаю ответ на вопрос (+) | | Что называют графиком функции? |
|
| | Какие два условия должны выполняться, чтобы фигура была графиком функции f? |
|
| | Может ли график функции состоять из одной точки? |
|
| | Любая ли фигура на координатной плоскости может служить графиком функции? |
|
| | Сколько общих точек может иметь с графиком функции любая прямая, перпендикулярная оси абсцисс? |
|
| Анализируют ответы на вопросы. Проводят дополнительное изучение нового материала. Задают вопросы учителю | Умение осуществлять актуализацию полученных знаний и умений
|
| VIII. Решение заданий | Задания: 1. (№ 822) На рисунке 24 ученика изображен график некоторой функции. Пользуясь графиком, найдите: 1) значение у, если х = –3,5; –1,5; 2; 4; 2) значения х, которым соответствуют значения у = –3; –1,5; 2; 3) значения аргумента, при которых значение функции равно нулю; 4) область определения и область значений функции; 5) значения аргумента, при которых значения функции положительные; 6) значения аргумента, при которых значения функции отрицательные.
2. (№ 824) Принадлежит ли графику функции 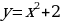 точка: точка: 1) А (0; 2); 3) С (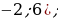 2) В (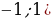 ; 4) D ( ; 4) D (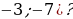 | Решение. 1. 1) 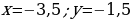 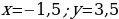 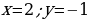 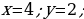 2) 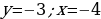 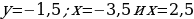 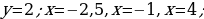 3) 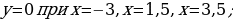 4) область определения: 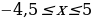 область значений: 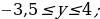 5) 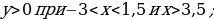 6) 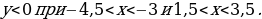
2.
1) принадлежит; 3) принадлежит; 2) не принадлежит; 4) не принадлежит | Умение самостоятельно принимать решения |
| IX. Подведение итогов урока. Рефлексия | Организует подведение итогов урока обучающимися. Способствует размышлению учащихся над вопросами: – Что нового я узнал на уроке? – Доволен ли я своей работой на уроке? – Какой вопрос я так и не задал учителю? – Хочу ли я поделиться полученными на уроке знаниями со своими друзьями? | Подводят итоги своей работы на уроке. Проводят самооценку, рефлексию. | Умение отслеживать цель учебной деятельности |
| X. Домашнее задание | Помогает учащимся выбрать задания из учебника. Обращает внимание на возможности и способности учащихся | Выбирают задания, которые будут решать дома. Записывают домашнее задание. | Формирование навыков самоорганизации |







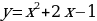 . При каких значениях х значение функции равно удвоенному значению аргумента?
. При каких значениях х значение функции равно удвоенному значению аргумента?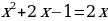
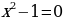
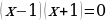
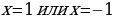
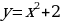 точка:
точка: 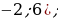
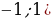 ; 4) D (
; 4) D (