Наслаждайтесь радостью окончания учебного года весь следующий! Доступ к материалами на весь год со скидкой 90%

СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ

Благодаря готовым учебным материалам для работы в классе и дистанционно

Выбрать материалы

Скидки до 50 % на комплекты
только до 17.06.2025

Готовые ключевые этапы урока всегда будут у вас под рукой

Организационный момент

Проверка знаний

Объяснение материала

Закрепление изученного

Итоги урока

Была в сети 28.09.2022 10:17

Фрольцева Валентина Тимофеевна

Учитель математики

74 года

2 074

29 441

Подписчики

Подписки

Местоположение

ЛНР, Вахрушево

Специализация

Математика

Классному руководителю

Всем учителям

Прочее

Алгебра

Геометрия

Обо мне Блог Файлы Тесты Галерея Активность Награды

Тела и поверхности вращения.

Категория: Геометрия

01.02.2021 20:03

Просмотр содержимого документа
«Тела и поверхности вращения.»

Тема: Тела и поверхности вращения.

Абитуриенту необходимо знать следующее:

Цилиндр. Основание, высота, боковая поверхность, образующая, развертка
Конус. Основание, высота, боковая поверхность, образующая, развертка
Шар и сфера, их сечения

Главная особенность всех упомянутых тел - наличие оси вращения, которая является осью симметрии тела. Если совместить оси вращения двух разных тел, то также получится некая осесимметричная конструкция, все сечения которой плоскостью, проходящей через эту ось, будут одинаковыми. Это позволяет быстро и легко переходить от задачи по стереометрии к рассмотрению плоского сечения.

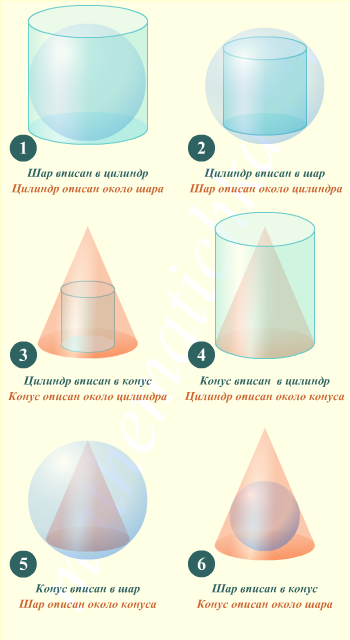
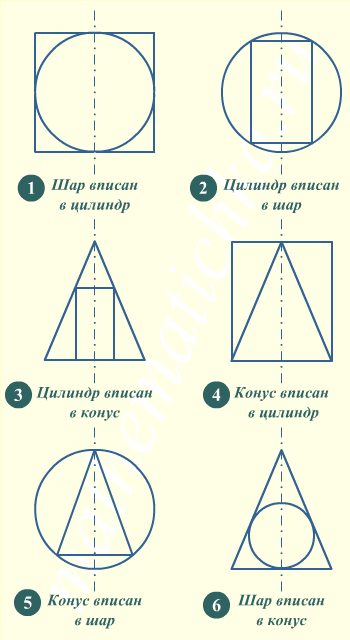
Поэтому в школьных учебниках, а также в заданиях ЕГЭ по математике часто встречаются задачи на вписанные и описанные тела вращения.

Могут потребоваться следующие формулы:

Объем цилиндра V = πr²h;

площадь боковой поверхности цилиндра S_б = 2πrh;
площадь полной поверхности цилиндра S_п= 2πrh + 2πr²,
где r - радиус основания цилиндра, h - его высота.

Объем конуса V = 1/3 πr²h;

площадь боковой поверхности конуса S_б = πrl;
площадь полной поверхности конуса S_п = πr(r + l),
где r - радиус основания конуса, l - длина образующей.

Объём шара V = 4/3πR³;

площадь сферы (поверхности шара) S = 4πR²,
где R - радиус шара (сферы).

Задачи на тела вращения

Задача 1

Цилиндр, объём которого равен 33, описан около шара. Найдите объём шара.

Задача 2

Шар вписан в цилиндр. Площадь поверхности шара равна 111. Найдите площадь полной поверхности цилиндра.

Задача 3

Цилиндр вписан в шар, радиус которого равен √2_. Найти объём цилиндра, если высота цилиндра в два раза больше радиуса цилиндра. Ответ записать в виде десятичной дроби с точностью до 0,01.

Задача 4

В шар, площадь поверхности которого равна 100π, вписан цилиндр. Найти высоту цилиндра, если радиус его основания равен 4.

Задача 5

Конус вписан в цилиндр. Вычислите объём цилиндра, если объём конуса равен 5.

Задача 6

Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна 3√2_. Найдите площадь боковой поверхности конуса.

Задача 7

В конус вписан цилиндр так, что его верхнее основание пересекает высоту конуса в её середине. Найдите объём конуса, если объем цилиндра равен 60.

Задача 8

В конус с высотой 15 и радиусом основания 3 вписан цилиндр объёма V. Найти наибольшее возможное значение объёма цилиндра.

Задача 9

Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы находится в центре основания конуса. Образующая конуса равна 7√2_. Найдите радиус сферы.

Задача 10

Найти площадь поверхности шара, описанного около конуса, у которого радиус основания 2__√π_,

а высота 1__√π_.

Задача 11

В шар вписан конус. Площадь осевого сечения конуса равна ³√9/π² _____, а угол между высотой и образующей равен 45°. Найти объём шара.

Задача 12

В шар вписан конус, образующая которого равна диаметру основания. Найти отношение полной поверхности этого конуса к поверхности шара.