Россия,
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 31.08.2025 21:29
Гончаренко Галина Петровна
учитель
58 лет
2 448
25 346 
Местоположение
Тема урока: Теорема Виета.
Категория:
Алгебра
20.03.2022 22:43
Просмотр содержимого документа
«Тема урока: Теорема Виета.»
Тема урока: Теорема Виета.
Планируемые результаты урока:
1.Предметные: изучить теорему Виета; формировать умение применять теорему Виета и обратную ей теорему при решении приведённых квадратных уравнений.
2.Метапредметные: уметь ориентироваться в своей системе знаний (отличать новое от уже известного с помощью учителя); добывать новые знания (находить ответы на вопросы, используя учебник,информацию, полученную на уроке);уметь осознанно и произвольно строить речевые высказывания; извлекать из математических текстов необходимую информацию;уметь планировать последовательность своих действий для достижения конечного результата;слушать и слышать друг друга.
3.Личностные: уметь осуществлять самооценку на основе критерия успешности учебной
деятельности; проявлять учебно-познавательный интерес к новому учебному материалу; ориентироваться на успех в учебной деятельности.
Ход урока:
1.Организационный этап.
Приветствие. Проверка готовности к уроку.
2. Мотивация учебной деятельности учащихся.
«Час, затраченный на понимание, экономит год жизни». Э. Босс.
3. Актуализация знаний
1)устная разминка.
Какое уравнение называют квадратным?
Какие виды квадратных уравнений вы знаете? Чем они отличаются?
Что такое корень уравнения?
От чего зависит количество корней квадратного уравнения?
Напишите формулу дискриминанта квадратного уравнения.
6.Напишите формулу корней квадратного уравнения
2). Назовите полные, неполные и приведённые квадратные уравнения:
а) 4х2 – х = 0; е) –х2 + х = 0;
б) 7х2 – 16х + 4 = 0; ж) х2 = 0;
в) х2 – 9 = 0; з) х2 + 6х + 9 = 0;
г) –х2 + 2х – 4 = 0; и) х2 = 16;
4. Самоопределение к деятельности, определение темы, постановка целей и задач урока.
Хочу напомнить вам: «Знания – самая прочная жизненная основа».
Особенно если эти знания добыты собственным трудом.
Сегодня на уроке вам предстоит сделать маленькое открытие.
5. Первичное усвоение новых знаний.
1. «О т к р ы т и е» теоремы Виета.
| Уравнение | b | c | Корни | Сумма корней | Произведение корней |
| х2 – 3х + 12 = 0 |
|
|
|
|
|
| х2 – х – 12 = 0 |
|
|
|
|
|
| х2 + 5х + 6 = 0 |
|
|
|
|
|
| Т е о р е м а В и е т а Если х1, х2 – корни уравнения x2 + px + q = 0, то х1 + х2 = –р; х1 · х2 = q. |
2. Т е о р е м а В и е т а для неприведённого квадратного уравнения.
| Т е о р е м а В и е т а Если х1, х2 – корни уравнения аx2 + bx + c = 0, то х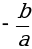1 + х2 = |
; х1 ∙ х2 =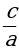 
.3. Т е о р е м а, обратная теореме Виета.(работа с учебником)
6. Первичное закрепление.
2) работа в парах № 580, № 582, № 583
3) Проверочная работа.
Найдите значение выражений х1 + х2 и х1 · х2:
В а р и а н т 1
а) х2 – 7х – 9 = 0; в) 5х2 – 7х = 0;
б) 2х2 + 8х – 19 = 0; г) х2 – 16 = 0.
В а р и а н т 2
а) х2 + 8х – 11 = 0; в) 4х2 + 9х =0;
б) 3х2 – 7х – 12 = 0; г) х2 – 25 = 0.
7. Информация о домашнем задании, инструктаж о его выполнении.
п.24(примеры) № 581(а,в), № 584.
8. Итоги урока: В о п р о с ы у ч а щ и м с я:
– Сформулируйте теорему Виета.
– Что необходимо проверить, прежде чем находить сумму и произведение корней приведённого квадратного уравнения?
– Как можно применить теорему Виета для неприведённого квадратного уравнения?
– В чём состоит теорема, обратная теореме Виета? Когда она применяется?
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
