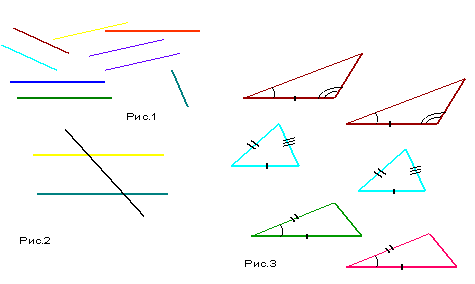"Теорема Фалеса"

Интегрированный урок (математика + информатика)

по теме: "Теорема Фалеса"

Цели урока:

Образовательная: доказать теорему Фалеса, научить применять её при решении задач по математике и информатике.

Развивающая: развивать у учащихся познавательный интерес к учебным дисциплинам, умение применять свои знания на практике.

Воспитательная: воспитывать внимание, аккуратность, расширять кругозор учеников.

Оборудование и материалы:

Компьютер, экран, проектор.
Проектная работа “Теорема Фалеса”.
Программа “Живая геометрия”.
Плакат с рисунками 1,2,3.

Задачи учителей:

Показать практическое применение теоретических знаний учащихся при решении задач по геометрии и информатике.

Выявить глубокие связи между математикой и информатикой.

Ход урока:

Урок начинает учитель математики. Приветствие и вступительное слово о целях урока.

Фронтальный опрос учащихся:

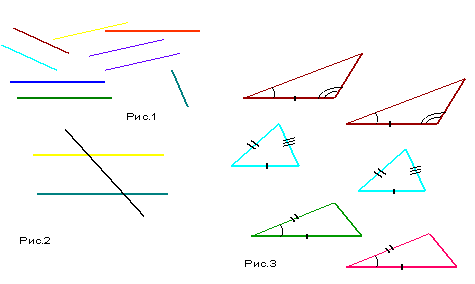
1. Какие отрезки называются равными?

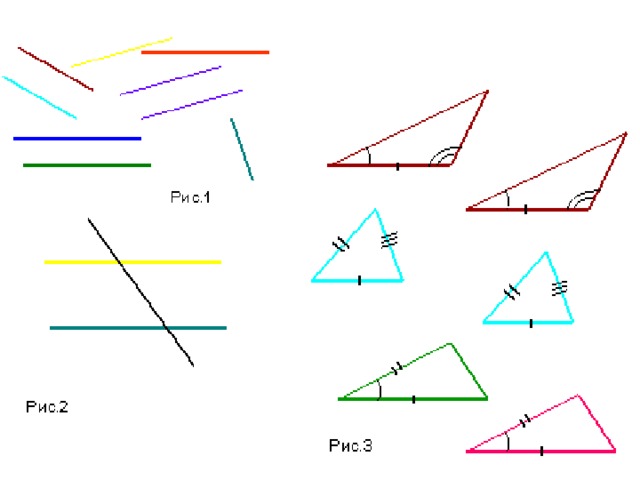
2. Какие прямые называются параллельными? На рис. 1 покажите параллельные прямые.

3. Какие углы называются вертикальными, внутренними накрест лежащими? Покажите их на рис.2

4. Сформулируйте теорему о свойстве параллельных прямых, пересечённых третьей прямой.

5. Сформулируйте признаки равенства треугольников. По каким признакам равны треугольники на рис 3?

Объяснение нового материала

Учитель математики объясняет новую тему с помощью просмотра проектной работы “Теорема Фалеса”.

(Приложение 1)

Сегодня мы докажем теорему, носящую имя древнегреческого учёного Фалеса, который жил в 624-547г.г. до н.э.

Великий учёный Фалес Милетский основал одну из прекраснейших наук - геометрию. Известно, что Фалес Милетский имел титул одного из семи мудрецов Греции, что он был поистине первым философом, первым математиком, астрономом и вообще первым по всем наукам в Греции. Короче: он был то же для Греции, что Ломоносов для России.

Карьеру он начинал как купец и ещё в молодости попал в Египет. В Египте Фалес застрял на много лет, изучая науки в Фивах и Мемфисе. Считается, что геометрию и астрономию в Грецию привёз он.

Фалес — математик. Он измерил по тени высоту пирамиды; установил, что окружность диаметром делится пополам, что углы при основании равнобедренного треугольника равны. Ему же принадлежит теорема, что вписанный угол, опирающийся на диаметр окружности- прямой.

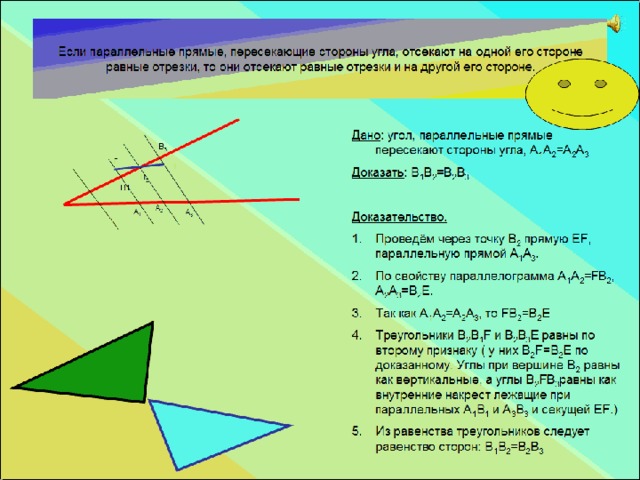
Фалес доказал теорему: “Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне”.

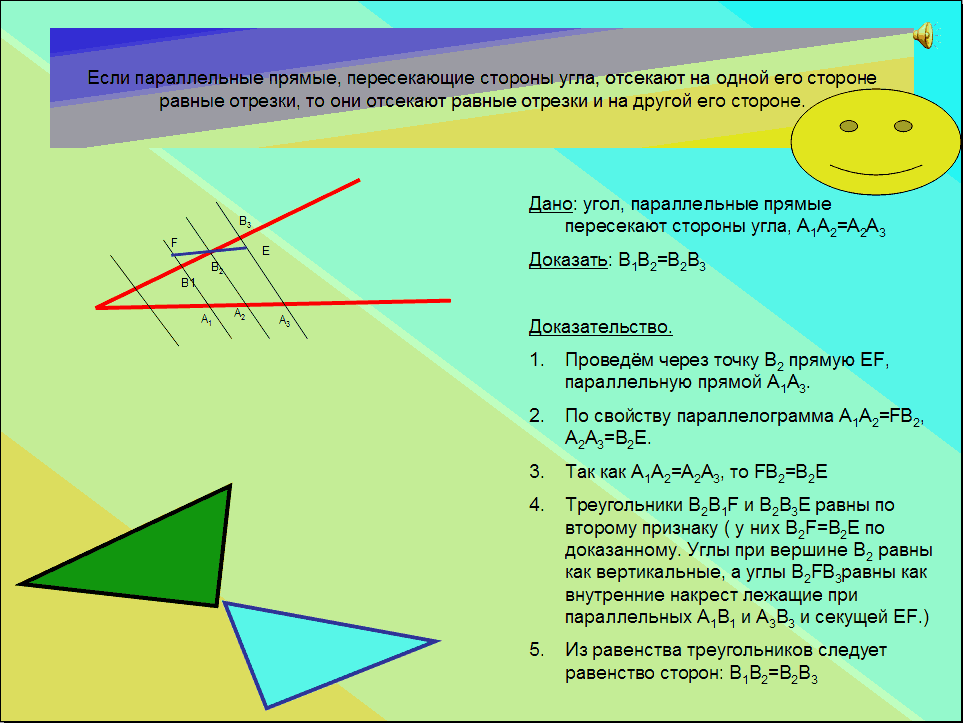
При активном участии учащихся разбирается доказательство теоремы с последовательным показом на экране каждого этапа построения чертежа и доказательства теоремы.

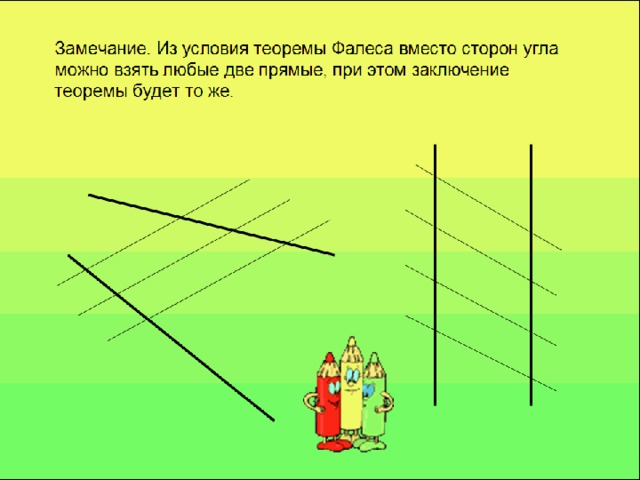
Из условия теоремы Фалеса делается вывод, что вместо сторон угла можно взять любые две прямые.

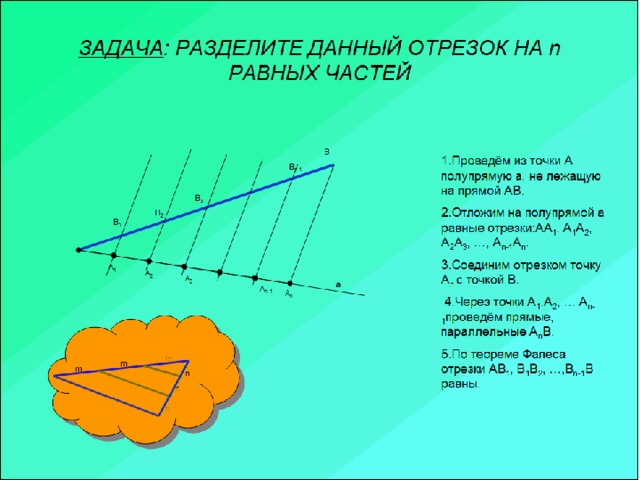
Затем ученики выполняют в тетрадях практическую задачу на деление отрезка длиной в 7см. на 6 равных частей.

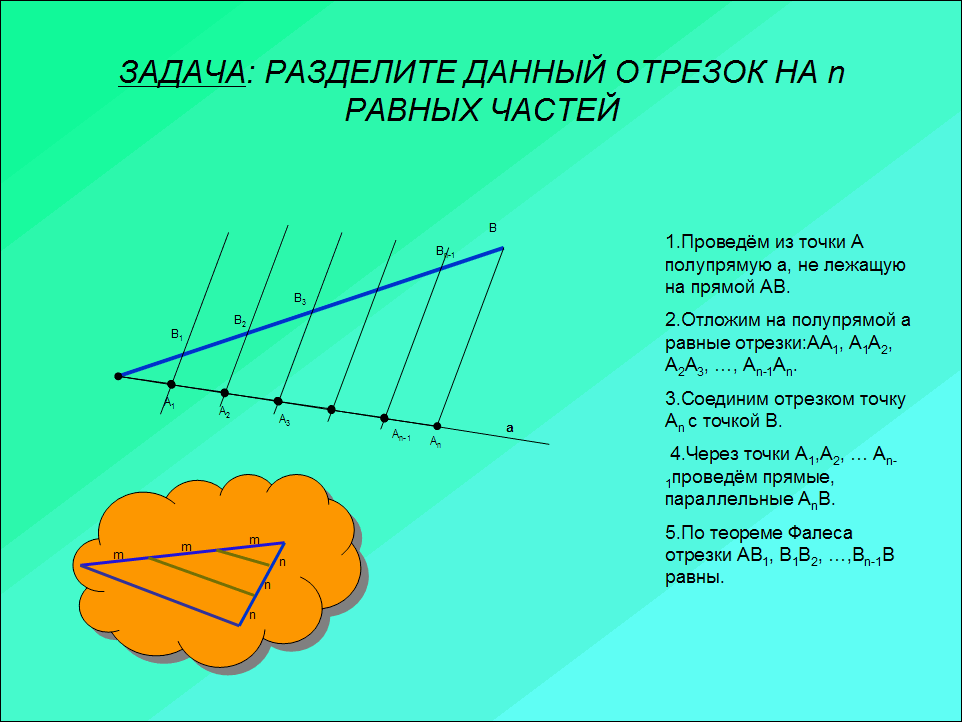
Греческие ученые открыли множество геометрических свойств и создали стройную систему геометрических знаний. В ее основу они положили простейшие геометрические свойства, подсказанные опытом. Остальные свойства выводились из простейших с помощью рассуждений.

Все этапы решения задачи учащиеся видят на экране. Это способствует зрительному запоминанию алгоритма решения данной задачи.

Показ проектной работы сопровождается музыкой- игрой на гитаре, что создаёт спокойную рабочую обстановку.

Вторую часть урока ведёт учитель информатики. С помощью программы “Живая геометрия” ученики вместе с учителем на компьютерах делят отрезок на три равные части.

Выполнение практического задания

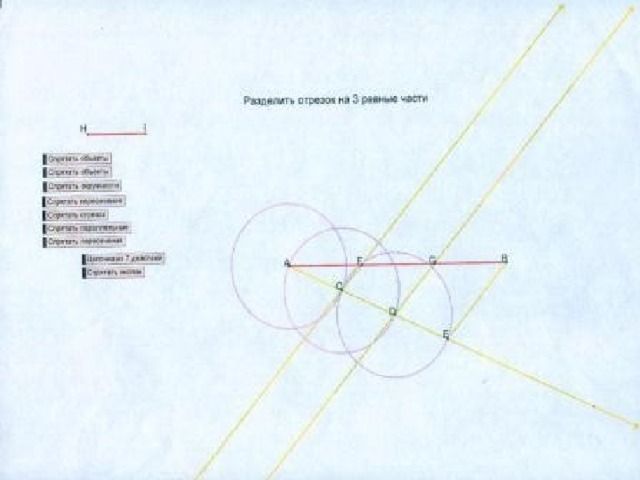
Разделить данный отрезок на 3-равные части на компьютере с помощью программы “Живая геометрия”.

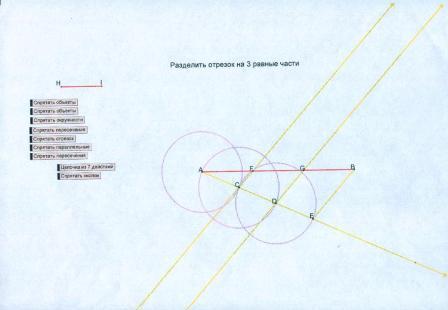
Используемые ИНСТРУМЕНТЫ “Живой геометрии”:

• стрелка;

• линейка (отрезок, луч).

Используемые КОМАНДЫ “Живой геометрии”:

• построения;

• правка;

Порядок работы:

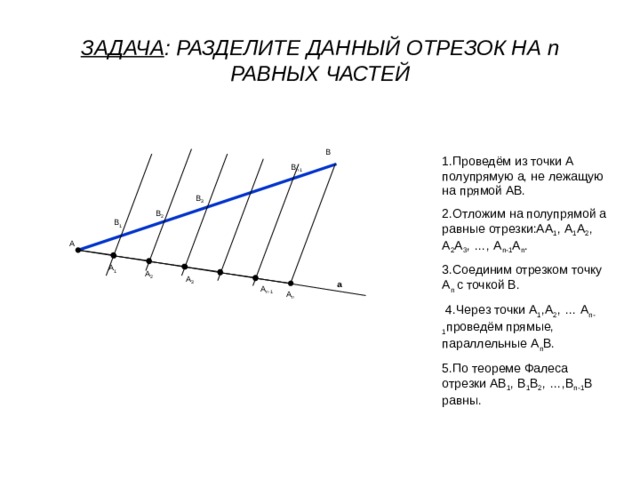
1 .Построим данный отрезок АВ.

2.Проведем из т. А полупрямую а, не лежащую на прямой АВ.

3.Отложим на полупрямой а 3 равных отрезка.

Для этого используем команду ПОСТРОЕНИЯ— “окружность по центру и радиусу”; зададим произвольный радиус СО и построим на полупрямой а 3 окружности.

Они отсекают на полупрямой а равные отрезки АЕ=ЕР=РО.

4.Соединим точки В и О.

5. Проведем через точки Е и Р прямые, параллельные прямой ВО.

6. Они пересекают отрезок АВ в точках Н и I , которые делят отрезок АВ на 3 равные части; т.к. по теореме Фалеса:

Если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Домашнее задание.

Задача: Разделить отрезок длиной 5 см. на 7 равных частей. Выучить теорему Фалеса.

Подведение итогов урока.

Приложение

Фалес Милетский

Карьеру он начинал как купец и ещё в молодости попал в Египет. В Египте Фалес застрял на много лет, изучая науки в Фивах и Мемфисе. Считается, что геометрию и астрономию в Грецию привёз он.

624-547г.г. до н.э.

Фалес- математик. Он измерил по тени высоту пирамиды; установил, что окружность диаметром делится пополам, что углы при основании равнобедренного треугольника равны. Ему же принадлежит теорема, что вписанный угол, опирающийся на диаметр окружности- прямой

• Великий учёный Фалес Милетский основал одну из прекраснейших наук- геометрию. Известно, что Фалес Милетский имел титул одного из семи мудрецов Греции, что он был поистине первым философом, первым математиком, астрономом и вообще первым по всем наукам в Греции. Короче: он был то же для Греции, что Ломоносов для России.

Теорема: если параллельные прямые, пересекающие стороны угла, отсекают на одной его стороне равные отрезки, то они отсекают равные отрезки и на другой его стороне.

Дано : угол, параллельные прямые пересекают стороны угла, А 1 А 2 =А 2 А 3

Доказать : В 1 В 2 =В 2 В 3

Доказательство.

• Проведём через точку В 2 прямую Е F , параллельную прямой А 1 А 3 .
• По свойству параллелограмма А 1 А 2 =F В 2 , А 2 А 3 =В 2 Е.
• Так как А 1 А 2 =А 2 А 3 , то F В 2 =В 2 Е
• Треугольники В 2 В 1 F и В 2 В 3 Е равны по второму признаку ( у них В 2 F= В 2 Е по доказанному. Углы при вершине В 2 равны как вертикальные, а углы В 2 F В 3 равны как внутренние накрест лежащие при параллельных А 1 В 1 и А 3 В 3 и секущей Е F .)
• Из равенства треугольников следует равенство сторон: В 1 В 2 =В 2 В 3

В 3

F

E

В 2

В1

А 2

А 1

А 3

ЗАДАЧА : РАЗДЕЛИТЕ ДАННЫЙ ОТРЕЗОК НА n РАВНЫХ ЧАСТЕЙ

В

1.Проведём из точки А полупрямую а, не лежащую на прямой АВ.

2.Отложим на полупрямой а равные отрезки:АА 1 , А 1 А 2 , А 2 А 3 , …, А n -1 А n .

3.Соединим отрезком точку А n с точкой В.

4.Через точки А 1 ,А 2 , … А n-1 проведём прямые, параллельные А n В.

5.По теореме Фалеса отрезки АВ 1 , В 1 В 2 , …,В n-1 В равны.

В n-1

В 3

В 2

В 1

А

А 1

А 2

А 3

а

А n-1

А n