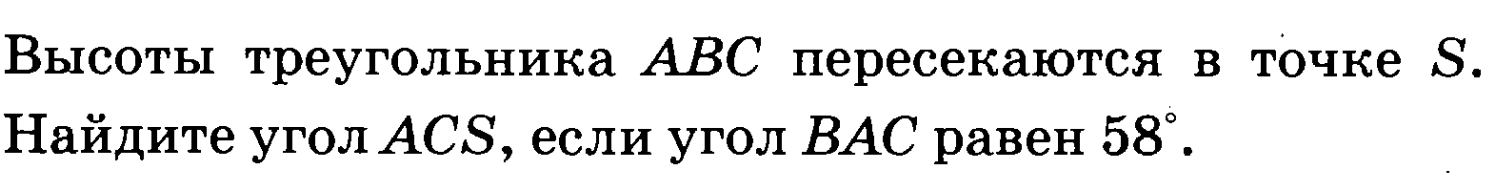Теорема о пересечении высот треугольника

Дата:

Тема: ТЕОРЕМА О ПЕРЕСЕЧЕНИИ ВЫСОТ ТРЕУГОЛЬНИКА

Задачи: рассмотреть теорему о точке пересечения высот треугольника, закрепить полученные знания в ходе решения задач.

Ход урока

1. АКТУАЛИЗАЦИЯ ЗНАНИЙ

Ответьте устно на вопросы:

1. Сформулируйте теорему о биссектрисе угла.

2. Какая прямая называется серединным перпендикуляром к отрезку?

3. Как звучит теорема о серединном перпендикуляре к отрезку?

4. Верно ли, что биссектрисы треугольника пересекаются в одной точке?

5. Верно ли, что серединные перпендикуляры к сторонам треугольника пересекаются в одной точке?

6. Верно ли, что медианы треугольника пересекаются в одной точке?

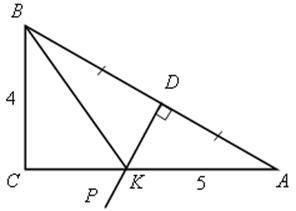
Решите устно задачу. Найти: Р_ВКС.

1. ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА

Откройте свои тетради и запишите сегодняшнее число и тему. Выполните конспект, приведенный ниже.

Вспомним, что высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противолежащую сторону. Высот в треугольнике 3.

 На рисунке BF — высота, проведенная из вершины B к стороне AC.

Теорема. Высоты треугольника (или их продолжения) пересекаются в одной точке. Эта точка называется ортоцентром треугольника.

Вспомним, что у нас есть 3 разных вида треугольника, если классифицировать их по углам. Существуют остроугольный, прямоугольный и тупоугольный треугольники. Применим теорему к каждому из них.

1. Пересечение высот в остроугольном треугольнике

Высоты остроугольного треугольника расположены строго внутри треугольника. Соответственно, точка Н пересечения высот также находится внутри треугольника (см. рисунок).

1. Пересечение высот в прямоугольном треугольнике

В прямоугольном треугольнике две высоты совпадают со сторонами (это высоты, проведенные из вершин острых углов к катетам). Высота, проведенная к гипотенузе, лежит внутри треугольника. Высоты прямоугольного треугольника пересекаются в вершине прямого угла А, точка А — ортоцентр (см. рисунок).

1. Пересечение высот в тупоугольном треугольнике

В тупоугольном треугольнике внутри треугольника лежит только одна высота — та, которая проведена из вершины тупого угла. Две другие высоты лежат вне треугольника и опущены к продолжению сторон треугольника.  AK — высота, проведенная к стороне BC. BF — высота, проведенная к продолжению стороны АС. CD — высота, проведенная к продолжению стороны AB.

Точка Н пересечения высот тупоугольного треугольника также находится вне треугольника. Точка H — ортоцентр треугольника ABC.

Чтобы лучше запомнить материал урока перейдите по ссылке и посмотрите видеоурок. Для 8-го класса он начинается на момент времени на видео 09:52.

http://1tvcrimea.ru/content/domashnee-zadanie-8-klass-literatura-geometriya-informatika-vypusk-ot-2042020

1. ПРАКТИЧЕСКАЯ ЧАСТЬ

Откройте учебники на странице 178 и выполним все вместе № 685. Прочтите внимательно условие задачи. Давайте выполним рисунок и оформим краткую запись к задаче.

№685

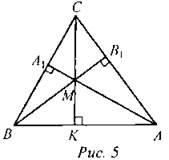
Дано: ∆АВС – равнобедренный, ВС=АС, АА₁ и ВВ₁ – высоты, АА₁ ∩ ВВ₁ = М, ВВ₁⊥ АС,

АА₁⊥ ВС.

Доказать: МС – серединный перпендикуляр к АВ (т.е. CM ⊥ BA, ВК = КА).

Доказательство:

1) Выполним дополнительное построение. Проведем высоту СК⊥ BA. Согласно изученной сегодня теореме она пройдет через точку М. СМ является частью высоты СК и так как АА₁∩ ВВ₁ = М и СК⊥ BA, то СМ ⊥ АВ.

2) Рассмотрим ∆ВСК и ∆АСК: сторона СК - общая, ВС = АС (по условию задачи), следовательно, ∆ВСК = ∆АСК (признак равенства треугольников по катету и гипотенузе). Следовательно, из равенства ∆ВСК = ∆АСК получим равенство ВК = КА, что и требовалось доказать.

Надеюсь, вы разобрались в доказательстве.

1. ПОДВЕДЕНИЕ ИТОГОВ УРОКА. РЕФЛЕКСИЯ

Какую теорему сегодня изучили?

Домашнее задание: выучить теорию, подготовиться к тесту + задачи.

Задача 1.

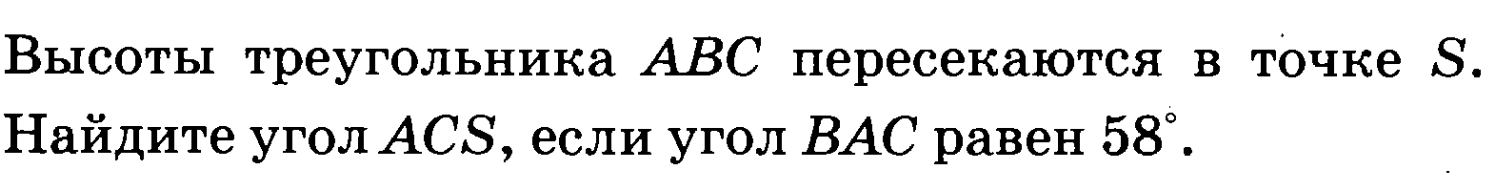
Задача 2.