Теорема о трех перпендикулярах

Теорема о трех перпендикулярах

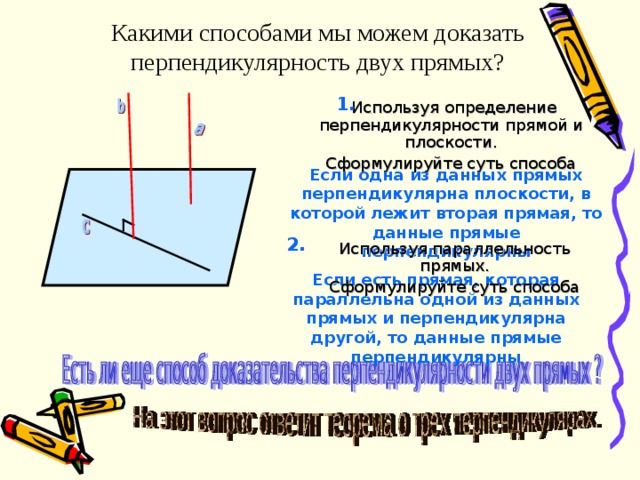
Какими способами мы можем доказать перпендикулярность двух прямых?

1.

Используя определение перпендикулярности прямой и плоскости.

Сформулируйте суть способа

Если одна из данных прямых перпендикулярна плоскости, в которой лежит вторая прямая, то данные прямые перпендикулярны

2.

Используя параллельность прямых.

Сформулируйте суть способа

Если есть прямая, которая параллельна одной из данных прямых и перпендикулярна другой, то данные прямые перпендикулярны

2

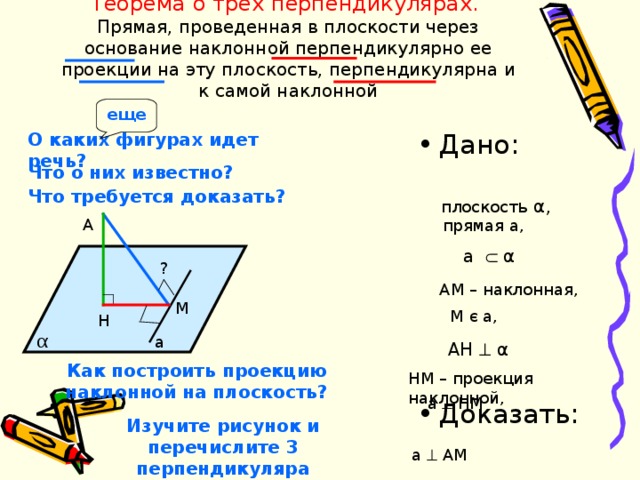
Теорема о трех перпендикулярах. Прямая, проведенная в плоскости через основание наклонной перпендикулярно ее проекции на эту плоскость, перпендикулярна и к самой наклонной

еще

• Дано:
• Доказать:

О каких фигурах идет речь?

Что о них известно?

Что требуется доказать?

плоскост ь α ,

A

прямая a ,

a  α

?

АМ – наклонная,

M

M є a ,

H

α

a

AH  α

Как построить проекцию наклонной на плоскость?

HM – проекция наклонной,

а  НМ

Изучите рисунок и перечислите 3 перпендикуляра

а  АМ

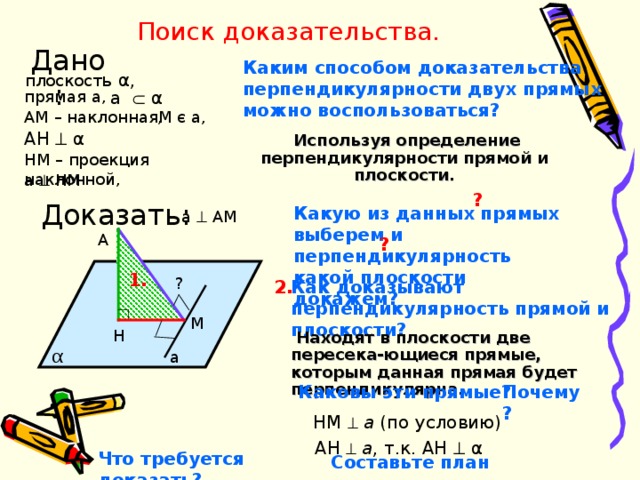
Поиск доказательства.

Дано:

Каким способом доказательства перпендикулярности двух прямых можно воспользоваться?

плоскост ь α ,

a  α

прямая a ,

M є a ,

АМ – наклонная,

AH  α

Используя определение перпендикулярности прямой и плоскости.

HM – проекция наклонной,

а  НМ

?

Доказать:

Какую из данных прямых выберем и перпендикулярность какой плоскости докажем?

а  АМ

A

?

1.

?

Как доказывают перпендикулярность прямой и плоскости?

2.

M

H

Находят в плоскости две пересека-ющиеся прямые, которым данная прямая будет перпендикулярна.

α

a

Каковы эти прямые?

Почему?

НМ  а (по условию)

АН  а , т.к. AH  α

Что требуется доказать?

Составьте план доказательства

Теорема о трех перпендикулярах.

Прямая, проведенная в плоскости через основание наклонной перпендикулярно к её проекции на эту плоскость, перпендикулярна и к самой наклонной.

Изучите в учебнике доказательство теоремы.

Доказательство:

Рассмотрим плоскость AMH .

Прямая а перпендикулярна к этой плоскости,

так как она перпендикулярна к двум

пересекающимся прямым АН и МН

(а перпендикулярна НМ по условию и

а перпендикулярна АН, так как

АН перпендикулярна плоскости).

Отсюда следует, что прямая а

перпендикулярна к любой прямой,

лежащей в плоскости АМН, в частности, а

перпендикулярна АМ.

Теорема доказана.

1.

2.

,

A

A

A

M

M

M

H

H

H

α

a

a

Выделите этапы доказательства

Какой способ используется для доказательства перпендикулярности прямых?

На чем основано доказательство перпендикулярности прямой и плоскости?

Теорема о трех перпендикулярах.

Прямая, проведенная в плоскости через основание наклонной перпендикулярно к её проекции на эту плоскость, перпендикулярна и к самой наклонной.

Оформите доказательство теоремы.

Доказательство:

1. Построим плоскость AMH .

2. Докажем, что прямая а  AMH .

а) а  НМ (по условию),

б) а  АН, т.к. АН  α , а  α ;

в) НМ ∩ АН = Н

Значит, а  AM (по определению прямой, перпендикулярной плоскости)

A

A

A

а  AMH

(по признаку)

?

M

M

M

H

H

H

α

a

a

Сравните свое оформление с приведенным. Какие выводы для себя можно сделать?

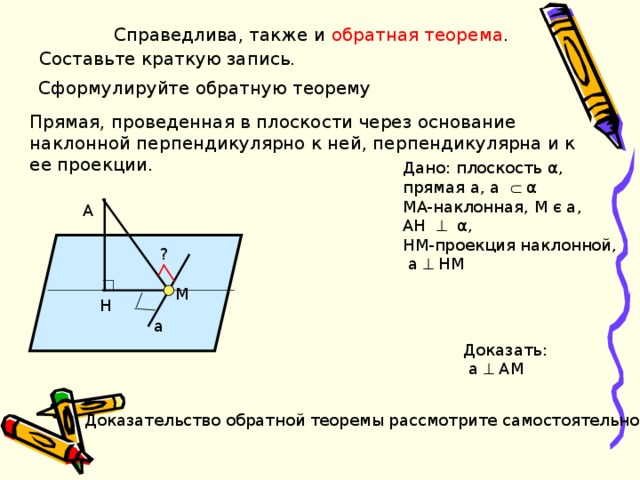
Справедлива, также и обратная теорема .

Составьте краткую запись.

Сформулируйте обратную теорему

Прямая, проведенная в плоскости через основание наклонной перпендикулярно к ней, перпендикулярна и к ее проекции.

Дано: плоскость α ,

прямая a , a  α

MA- наклонная, M є a ,

AH  α ,

HM -проекция наклонной,

а  НМ

A

?

M

H

H

a

Доказать:

а  АМ

Доказательство обратной теоремы рассмотрите самостоятельно

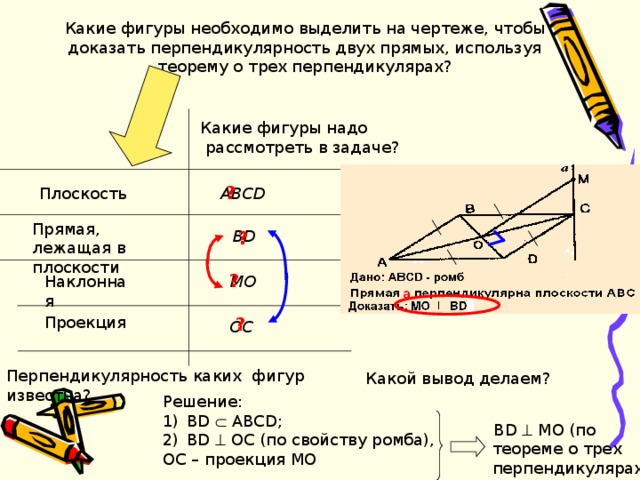
Какие фигуры необходимо выделить на чертеже, чтобы доказать перпендикулярность двух прямых, используя теорему о трех перпендикулярах?

Какие фигуры надо

ра c смотреть в задаче?

?

АВС D

Плоскость

Прямая, лежащая в плоскости

В D

?

?

Наклонная

M О

Проекция

?

OC

Перпендикулярность каких фигур известна?

Какой вывод делаем?

Решение:

• В D  АВС D ;
• В D  ОС (по свойству ромба),

ОС – проекция МО

В D  МО (по теореме о трех перпендикулярах),