Теорема Пифагора и её применение

Тема: «Теорема Пифагора и её практическое применение»

Цель урока: Сформировать УУД. Сформировать мотивацию к обучению. Рассмотреть способы решения типовых задач на применение теоремы Пифагора и метрических соотношений в прямоугольном треугольнике. Найти практическое применение теоремы Пифагора.

Задачи:

• узнать, о Пифагорейской школе;

• отработать навыки применения теоремы для решения задач;

• показать практическую значимость теоремы Пифагора;

• развитие мировоззрения учащихся, алгоритмического, комплексного мышления;

• воспитание активности, самостоятельности, ответственности, культуры общения, развитие коммуникативных способностей.

Формируемые УУД

• Личностные: учатся замечать и признавать свои ошибки, прислушиваться к мнениям одноклассников, анализировать, овладевать историческими и математическими знаниями и умениями, навыками их применения в реальной жизни, осознавать ценности исторических и математических знаний как важнейшего компонента научной картины мира, рефлексия.

• Коммуникативные: планирование учебного сотрудничества с учителями и сверстниками, приобретают умения организовать сотрудничество с партнёром, осуществлять оценку действий партнера, умение с достаточной полнотой и точностью выражать свои мысли.

• Регулятивные: осознание качества и уровня усвоения пройденного материала. Оценивают умение сотрудничать с учителем и одноклассниками.

• Познавательные: устанавливают причинно-следственные связи между объектами, осуществляют подведение под понятие, проводят сравнение, классификацию объектов, выбирают наиболее эффективный способов решения задач.

Планируемые образовательные результаты

• Метапредметные. Понимать связь математики с искусством, поэзией, философией, научиться чувствовать красоту формул и теорем, развивать интерес к истории математических открытий.

• Личностные. Грамотно излагать свои мысли, анализировать, сравнивать, развивать познавательный интерес через творческие задания. Уметь самостоятельно приобретать новые знания и практические умения, управлять своей познавательной деятельностью. Развивать активность и находчивость при решении поставленных задач, умение работать в коллективе. 

• Предметные. Понимать, что такое «теорема Пифагора» и метрические соотношения в прямоугольном треугольнике. Знать, как найти неизвестную сторону прямоугольного треугольника при помощи теоремы Пифагора или метрических соотношений в прямоугольном треугольнике.

Тип урока: Обобщение и систематизация знаний.

Формы работы учащихся: фронтальная, индивидуальная, парная.

Необходимое техническое оборудование: компьютер, интерактивное оборудование.

Дидактические средства: учебник, презентация, тест.

Методы и приемы: фронтальная работа, сочетающаяся с общеклассной; частично-поисковый метод; индивидуальная работа, работа парами.

«Не делай никогда того, чего не знаешь, но научись всему, что нужно знать»

Пифагор

Ход урока

1. Оргмомент

2. Актуализация знаний учащихся

Решение задач по готовому чертежу (слайды презентации)

В это время несколько человек работают по индивидуальному заданию (с низким уровнем обученности карточки с подсказкой)

Открыть тетради и записать тему урока: «Теорема Пифагора и её практическое применение»

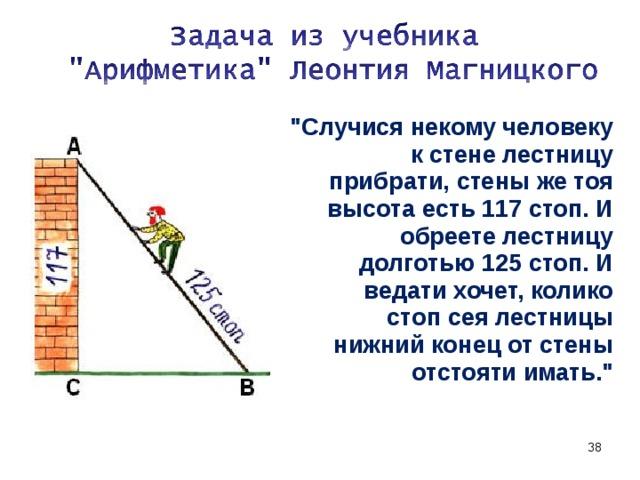
Решение задач: Задача Магницкого (слайд № 6) и из учебника №850.

Русский математик в 1703 году напечатал свою «Арифметику», которая до середины 18 века была основным учебником математики в России.

Решение:

=(125-117) ×(125+117)=

=8×242= 4 2×2×121

СВ= =2×2×11=44

Ответ: 44стопы

Начинают решать самостоятельно, предварительно проанализировав чему равна гипотенуза и известный катет и как найти неизвестный катет, затем вычисления у доски (рациональный способ).

№ 850 решение у доски.

Задача 6:

Мобильная связь

В настоящее время на рынке мобильной связи идет большая конкуренция среди операторов. Чем больше зона покрытия, тем надежнее связь, тем больше потребителей у оператора. При строительстве вышки (антенны) часто приходится решать задачу: какую наибольшую высоту должна иметь антенна, чтобы передачу можно было принимать в определенном радиусе (например, радиусе r =200 км?, если известно, что радиус Земли равен 6380 км.)

Р ешение:

Пусть AB= x, АC= r =200 км, OC= R =6380 км

OА = OВ + AB

OА = R + x

Используя теорему Пифагора, получим ответ.

Ответ: 0,3 км.

Задача 7:

Как рассчитать высоту шкафа-купе?

На первый взгляд ничего особенного: снять размеры высоты от пола до потолка в нескольких точках, отнять несколько сантиметров, чтобы шкаф не упирался в потолок. Поступив так, в процессе сборки мебели могут возникнуть трудности. Ведь сборка каркаса мебельщики выполняют, располагая шкаф в горизонтальном положении, а когда каркас собран, поднимают его в вертикальное положение. Рассмотрим боковую стенку шкафа. Высота шкафа должна быть на 10 см меньше расстояния от пола до потолка при условии, что это расстояние не превышает 2500 мм. А глубина шкафа – 700 мм. Почему на 10 см, а не на 5 см или на 7, и причем здесь теорема Пифагора?

Итак: боковая стенка 2500-100=2400(мм)- максимальная высота конструкции.

Боковая стенка в процессе подъема каркаса должна свободно пройти как по высоте, так и по диагонали. По теореме Пифагора

АС= √ АВ2 + ВС2

АС= √ 24002+ 7002 = 2500 (мм)

Что произойдет если высоту шкафа уменьшить на 50 мм?

АС= √ 24502+ 700 2= 2548 (мм)

Диагональ 2548 мм. Значит, шкаф не поставишь (можно испортить потолок).

Задача 8:

С аэродрома вылетели одновременно два самолета, один на юг, другой на запад. Через 2 часа расстояние между самолетами было равно 2000 км. Найдите сумму скоростей самолетов, если скорость одного самолета была равна 75% скорости второго самолета.

Решение:

Сперва требуется определить скорость отдаления самолетов.

Для этого делим известное расстояние между самолетами на время в полете.

Получим:

2000 / 2 = 1000 км/ч.

Представим скорость первого самолета как х км/ч. Поскольку скорость второго самолета составляет 75% от скорости первого, его скорость будет равна: 0,75 * х.

Получим уравнение:

х + 0,75 * х = 1000.

1,75 * х = 1000.

х = 571,4 км/ч.

Находим скорость второго самолета:

571,4 * 0,75 = 428,6 км/ч.

Проверка решения:

428,6 / 571,4 = 0,75.

Ответ: сумма скоростей 1000 км/ч.

Задача 9:

Случай из следственной практики.

Получив сообщение о краже, следователь выехал на место происшествия. Заявитель утверждал, что преступник проник в помещение, где хранились ценности, через окно. Осмотр показал, что подоконник находится на расстоянии124 см от земли, поверхность земли на расстоянии 180 см от стены покрыта густой порослью, не имеющей никаких следов повреждений.

Возникло предположение, что преступник проник в помещение через окно, каким-то образом преодолел расстояние между наружным краем поросли и подоконником. Оно было определено с применением теоремы Пифагора.

Решение:

? с = = ≈ 219 см.

124см

180 см

Очевидно, что преодолеть такое расстояние без какого-либо средства, например, лестницы, невозможно. Поиски этого средства не увенчались успехом.

С учётом этого обстоятельства и некоторых других данных, следователь выдвинул версию об инсценировке кражи, которая в ходе дальнейшего расследования подтвердилась.

Так школьная геометрия помогла следствию.

Выступление ученика о пифагорейской школе

Пифагорейцами было сделано много важных открытий в арифметике и геометрии, в том числе:

• теорема о сумме внутренних углов треугольника;

• построение правильных многоугольников и деление плоскости на некоторые из них;

• геометрические способы решения квадратных уравнений;

• деление чисел на чётные и нечётные, простые и составные; введение фигурных, совершенных и дружественных чисел;

• доказательство того, что не является рациональным числом;

• создание математической теории музыки и учения об арифметических, геометрических и гармонических пропорциях и многое другое.

Известно также, что кроме духовного и нравственного развития учеников Пифагора заботило их физическое развитие. Он не только сам участвовал в Олимпийских играх и два раза побеждал в кулачных боях, но и воспитал плеяду великих олимпийцев.

Около сорока лет учёный посвятил созданной им школе и, по одной из версий, в возрасте восьмидесяти лет Пифагор был убит в уличной схватке во время народного восстания.

Вот некоторые из 325 Пифагоровых заповедей:

• Мысль – превыше всего между людьми.

• Юноша! Если ты желаешь себе жизни долгоденственной, то воздержи себя от пресыщения и всякого излишества.

• Юные девицы! Помятуйте, что лицо лишь тогда бывает прекрасным, когда оно изображает изящную душу.

• Не гоняйся за счастьем: оно всегда находится в тебе самом.

• Делай лишь то, что впоследствии не омрачит тебя и не заставит раскаиваться.

• Не делай никогда того, чего не знаешь, но научись всему, что нужно знать.

• Не пренебрегай здоровьем своего тела.

• Научись жить просто и без роскоши.

• Либо молчи, либо говори то, что ценнее молчания.

• Не закрывай глаза, когда хочешь спать, не разобравши всех своих поступков за день.

• По торной дороге не ходи – следуй не мнениям толпы, а мнениям немногих понимающих.

Домашнее задание: «Якласс» проверочная работа «Теорема Пифагора» подготовка к контрольной работе

Решение тестов на отдельных листиках по группам (А и В – с низким уровнем обученности) (Приложение 1).

Рефлексия. Притча: шёл мудрец, а навстречу ему 3 человека, которые везли под горячим солнцем тележки с камнями для строительства. Мудрец остановился и задал каждому по вопросу. У первого спросил: «Что ты делал целый день?» И тот с ухмылкой ответил, что целый день возил тяжелые камни. У второго мудрец спросил: «А что ты делал целый день?» и тот ответил «А я выполнял свою работу». А третий улыбнулся, его лицо засветилось радостью и удовольствием «А я принимал участие в строительстве храма».

Ребята, давайте мы попробуем с вами оценить каждый свою работу за урок.

Кто возил камни? Кто выполнял свою работу? Кто строил храм?