Урок "Теорема Пифагора и ее применение при решении задач" Дата_18.02.25
Тип урока: урок обобщения и систематизации знаний;
Цель урока:
- совершенствовать навыки решения задач на нахождение площади, длины;
- раскрыть закономерности решения типовых задач на применение теоремы Пифагора, исследовать разные способы решения,
- создать условия для выработки навыков работы по алгоритму, составления алгоритмов и организации решения с их помощью;
-способствовать приобретению умения решать задачи из ОГЭ;
- создать условия для развития наблюдательности, умения в задачах практической направленности находить геометрические объекты и работать с ними.
Задачи урока:
общеобразовательные:
расширить и углубить знания учащихся о теореме Пифагора, совершенствовать навыки решения задач.
развивающие:
развитие памяти учащихся; умений преодолевать трудности при решении математических задач; познавательного интереса учащихся; развитие культуры устной и письменной речи.
воспитательные:
воспитание устойчивого интереса к предмету через решение различных задач, умения работать в коллективе.
Оборудование: компьютер; мультимедийный проектор; интерактивная доска; раздаточный материал.
План урока
Организационный момент. (1 мин)
Постановка цели урока. (1 мин)
Актуализация знаний (10 мин)
Работа в группах. (10 мин)
Самостоятельное решение задач. (10 мин)
Подведение итогов урока и оценка ответов учащихся. (1 мин)
Домашняя работа (1 мин)
Рефлексия. (1 мин)
Ход урока.
Организационный этап. Мотивация учащихся .
Учитель приветствует учащихся, проверяет их готовность к уроку: «Здравствуйте, ребята, садитесь! Улыбнитесь друг другу, мысленно пожелайте хорошего настроения!»
II. Постановка цели урока.
Я хочу начать урок со стихотворения: Если дан нам треугольник, и притом с прямым углом, то квадрат гипотенузы мы всегда легко найдем: катеты в квадрат возводим, сумму степеней находим - и таким простым путём к результату мы придём. О какой теореме идет речь? (теорема Пифагора)
Прежде чем перейти к следующему этапу, мне хотелось бы рассказать, как изначально звучала теорема Пифагора.

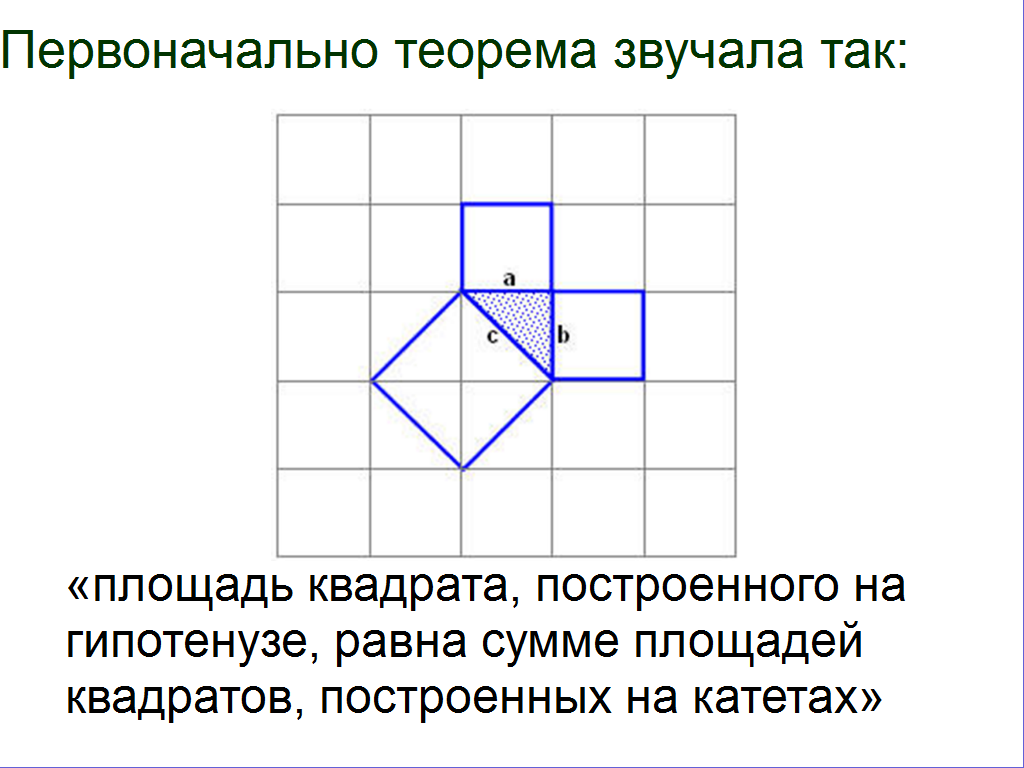
Доказательство теоремы Пифагора считалось в кругах учеников средних веков очень трудным и иногда называлось «ослиным мостом» или «бегством убогих» так как некоторые ученики бежали от геометрии, не пытаясь понять, а зазубривая доказательство. Поэтому возникали различные карикатуры, сопровождающие чертежи к доказательству теоремы. До сих пор не известно, сколько существует доказательств теоремы Пифагора. По одним источникам их более ста, по другим более 250, по третьим – долее 350 доказательств.
Наша цель: вспомнить изученный материал по теме “Теорема Пифагора” для применения при решении последующих задач.
Ш. Актуализация знаний.
Вот сейчас мы и проверим, насколько уверенно вы ориентируетесь в теореме Пифагора.
Напомните, пожалуйста, формулировку теоремы Пифагора. (ответы учащихся)
А обратная теорема? (ответы учащихся)
Чему равна площадь прямоугольного треугольника? Прямоугольника? Трапеции?
Затем учащимся предлагается решить задачи, на готовых чертежах, которые последовательно появляются на интерактивной доске.
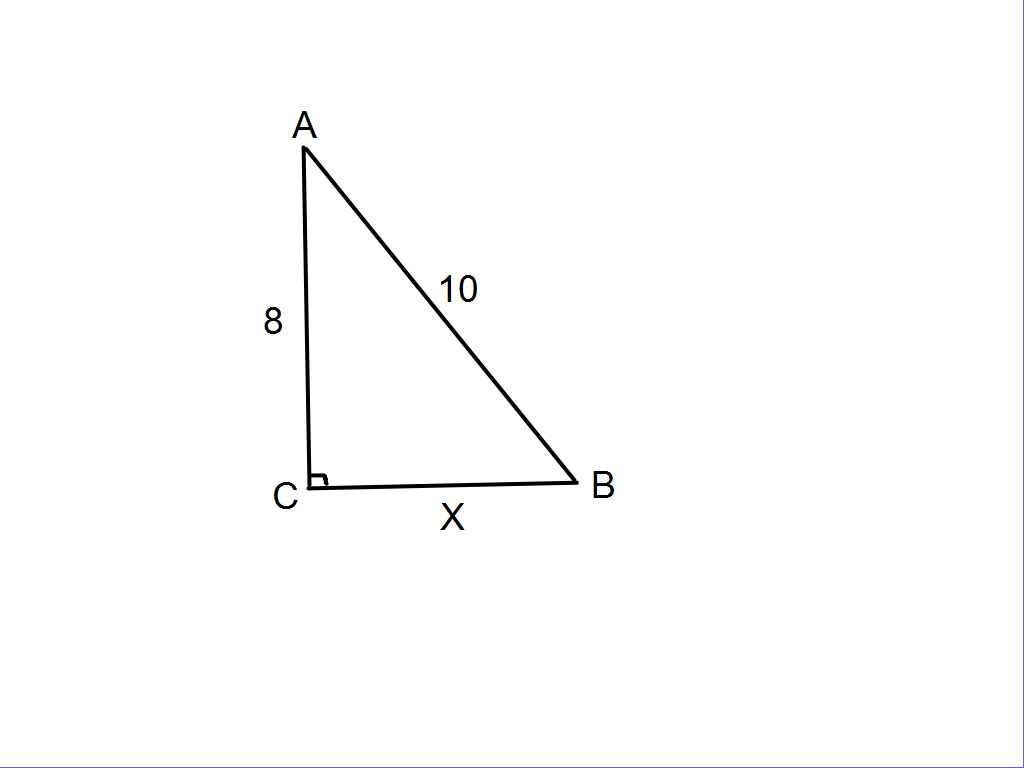
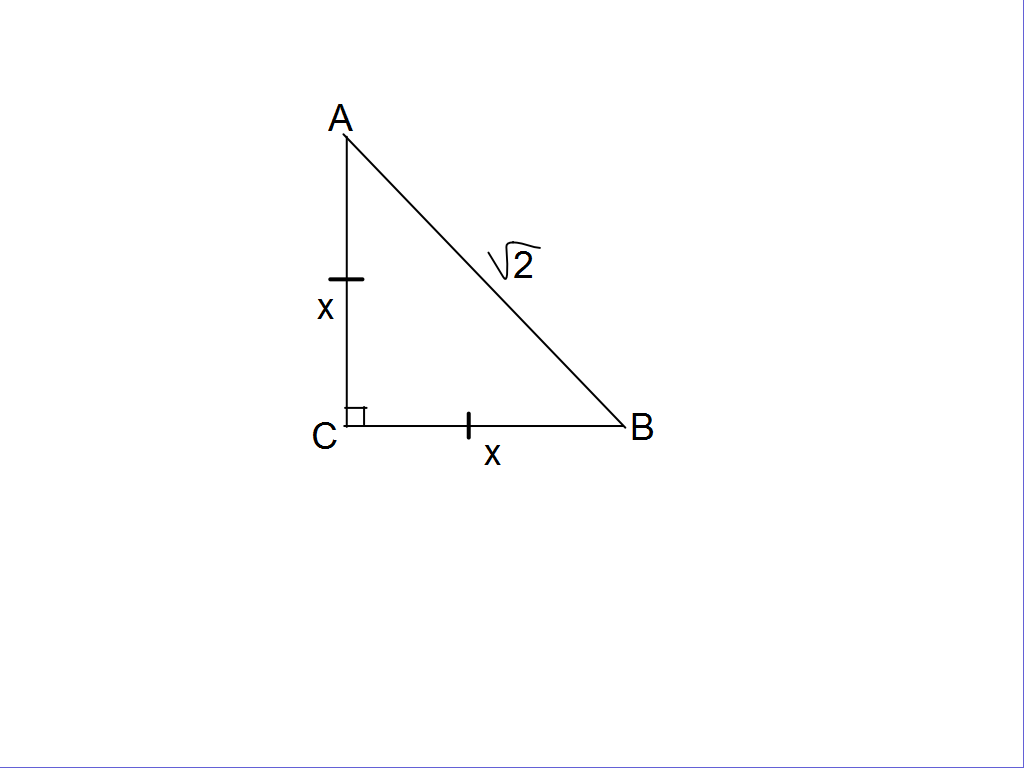
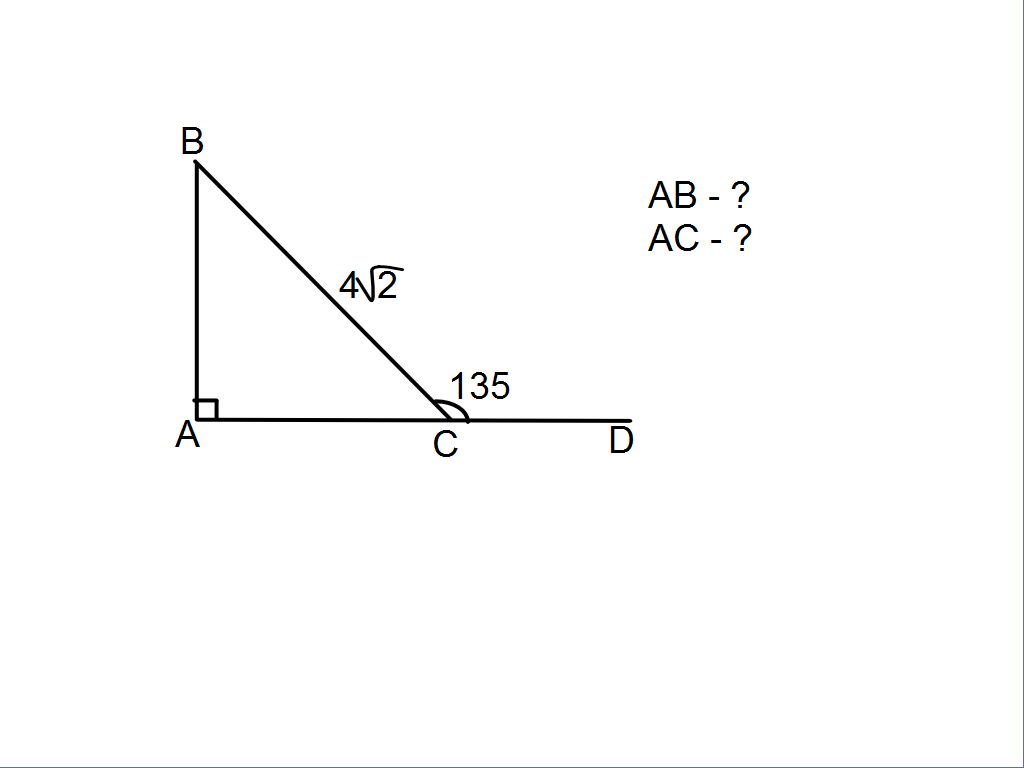
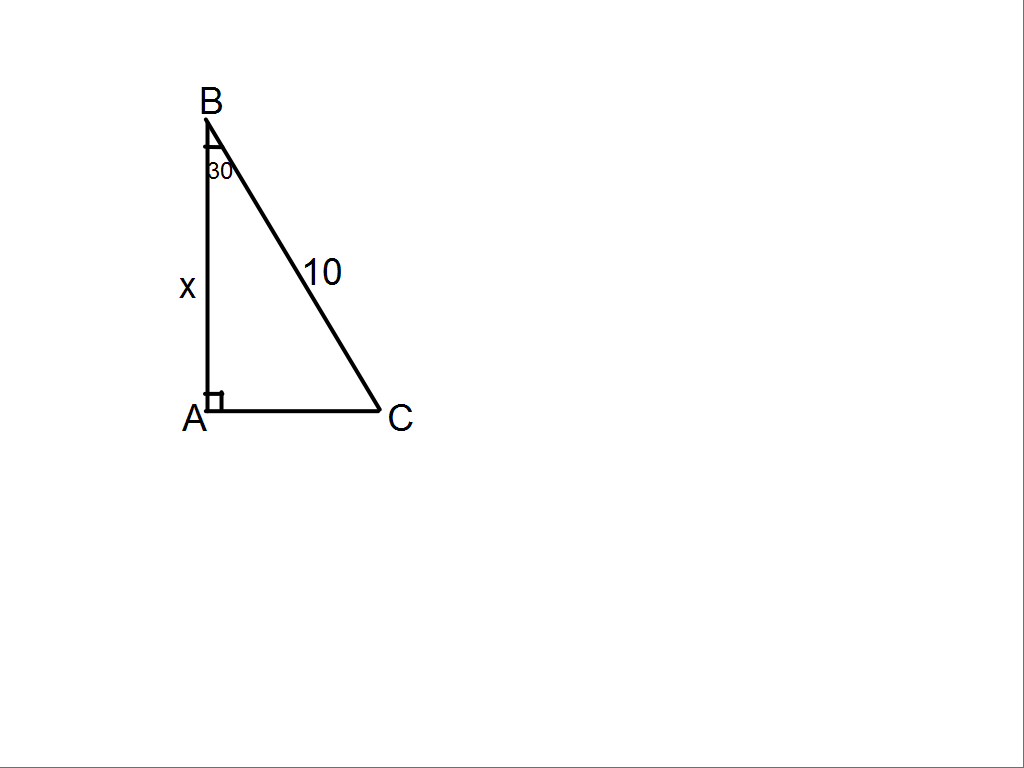
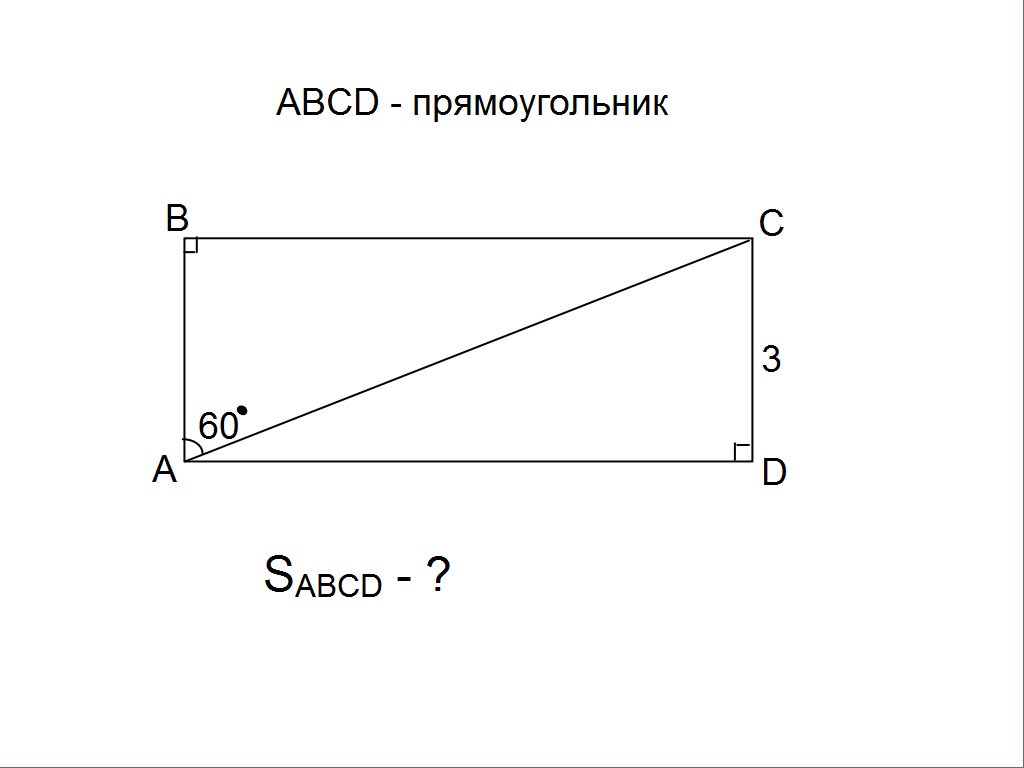
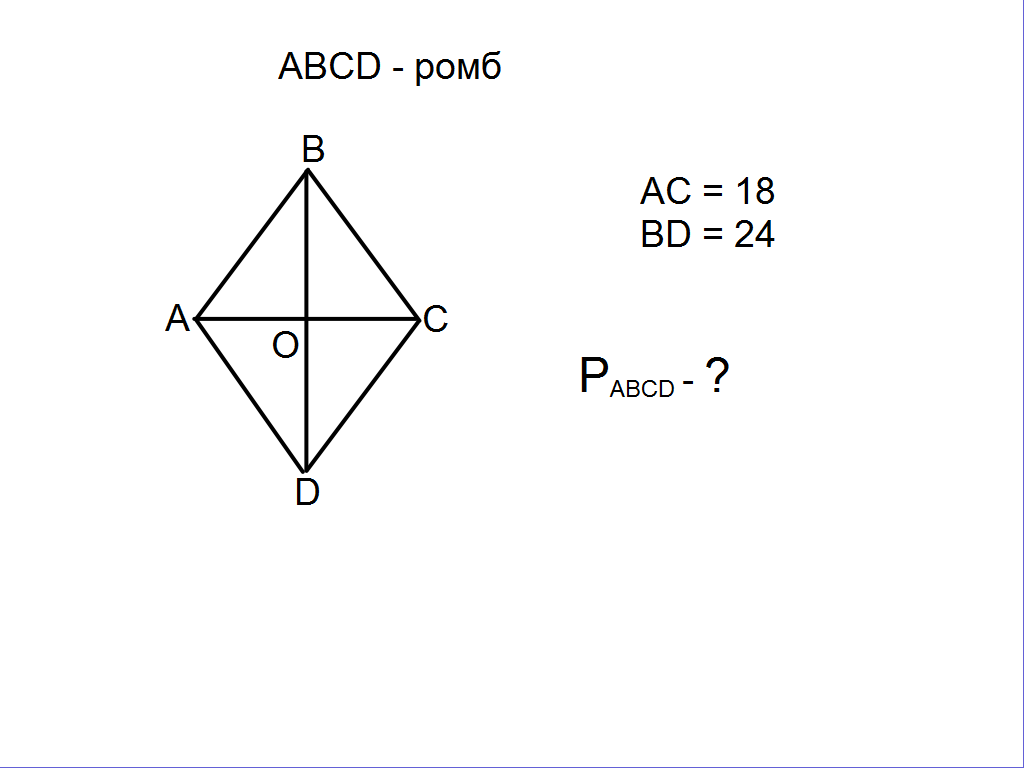
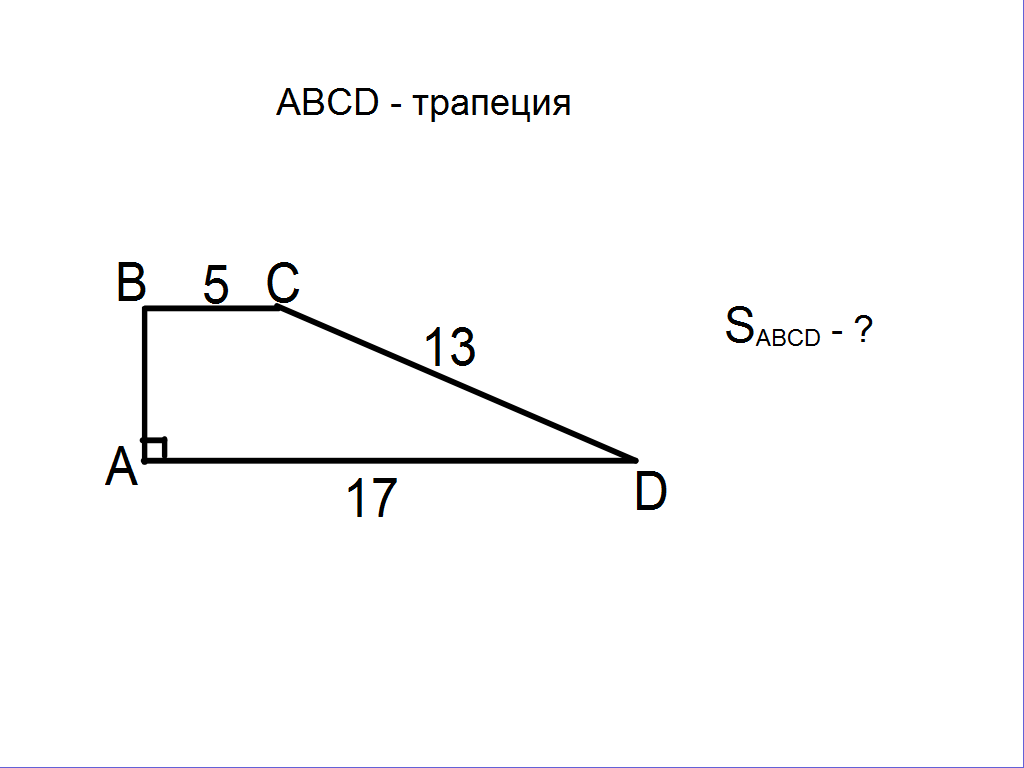
Учитель: “Вы хорошо потрудились, мы с вами вспомнили все то, что пригодится нам при решении последующих задач”.
IVРешение задач. Групповая работа
Цель: установить, усвоили или нет учащиеся материал, устранить обнаруженные пробелы.
Каждой группе предлагается на выбор по две задачи.
З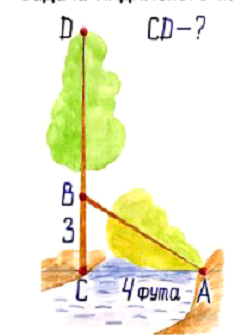 адача №1
адача №1
Историческая задача индийского математика XIIвека Бхаскары:
На берегу реки рос тополь одинокий.
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямой
С течением реки его ствол составлял.
Запомни теперь, что в этом месте река.
В четыре лишь фута была широка
Верхушка склонилась у края реки.
Осталось три фута всего от ствола, прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?
Задача 2.
 Задача о бамбуке из древнекитайского трактата «Гоу - гу»
Задача о бамбуке из древнекитайского трактата «Гоу - гу»
Имеется бамбук высотой в 1 чжан. Вершину его согнули так, что она касается земли на расстоянии 3 чм от корня. Какова высота бамбука после сгибания? 1 чжан = 10 чи
Задача №3
В древней Индии был обычай предлагать задачи в стихах
Н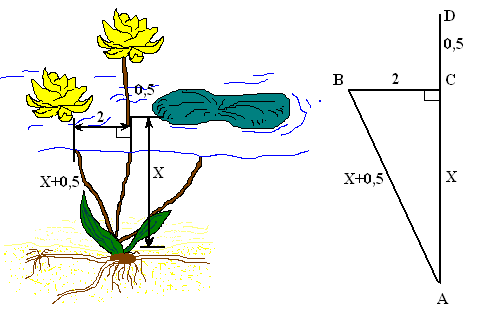 ад озером тихим
ад озером тихим
С полфута размером
Высился лотоса цвет.
Он рос одиноко,
И ветер порывом
Отнёс его в сторону. Нет
Боле цветка над водой.
Нашёл же рыбак его
Ранней весною
В двух футах от места, где рос.
Итак, предложу я вопрос:
“Как озера вода здесь глубока?”
Пожарную лестницу длиной 17 м приставили к окну шестого этажа дома. Нижний конец лестницы отстоит от стены на 8 м. На какой высоте расположено окно? Ответ дайте в метрах
З 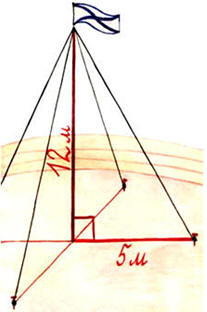 адача №4
адача №4
Для крепления мачты нужно установить 4 троса. Один конец каждого троса должен крепиться на высоте 12 м, другой на земле на расстоянии 5 м от мачты.
Хватит ли 50 м троса для крепления мачты?
З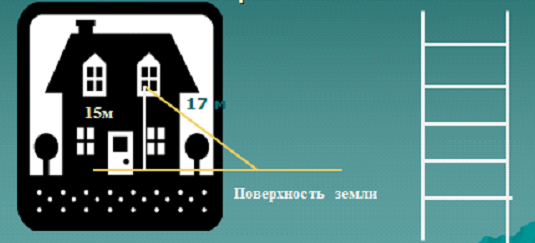 адача №5
адача №5
На каком расстоянии надо отодвинуть от стены дома нижний конец лестницы длиною 17 м, чтобы верхний конец лестницы её достал до слухового окна, находящегося на высоте 15 м от поверхности земли?
Учитель: “Вы замечательно поработали! Общими усилиями мы справились с решением всех задач”.
Переходим к следующему этапу урока – закрепление.
V. Самостоятельное решение задач
Цель: повторить, систематизировать и проверить знания учащихся по данной теме.
У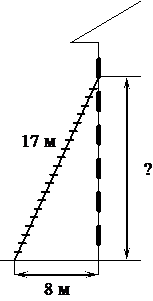 читель: “А теперь каждый попробует самостоятельно решить следующие задачи. Откуда я их взяла? Ни для кого не секрет, что в следующем году вы будете сдавать экзамен по математике в форме ГИА. И наверняка вам уже известно, что задания там будут не только по алгебре, но также и по геометрии. Так вот. Попробуйте решить некоторые из этих задач, которые я взяла из сборника по подготовке к ОГЭ по математике”. На интерактивной доске последовательно появляются три задачи.
читель: “А теперь каждый попробует самостоятельно решить следующие задачи. Откуда я их взяла? Ни для кого не секрет, что в следующем году вы будете сдавать экзамен по математике в форме ГИА. И наверняка вам уже известно, что задания там будут не только по алгебре, но также и по геометрии. Так вот. Попробуйте решить некоторые из этих задач, которые я взяла из сборника по подготовке к ОГЭ по математике”. На интерактивной доске последовательно появляются три задачи.
З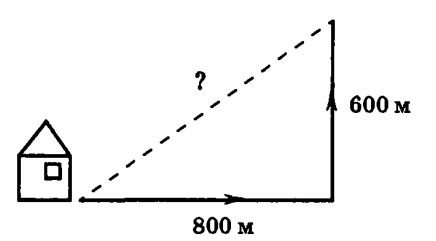 адача№1. Пожарную лестницу длиной 17 м приставили к окну шестого этажа дома. Нижний конец лестницы отстоит от стены на 8 м. На какой высоте расположено окно? Ответ дайте в метрах
адача№1. Пожарную лестницу длиной 17 м приставили к окну шестого этажа дома. Нижний конец лестницы отстоит от стены на 8 м. На какой высоте расположено окно? Ответ дайте в метрах
Задача№2 Мальчик прошёл от дома по направлению на восток 800 м. Затем повернул, а север и прошёл 600 м. На каком расстоянии (в метрах) от дома оказался мальчик?
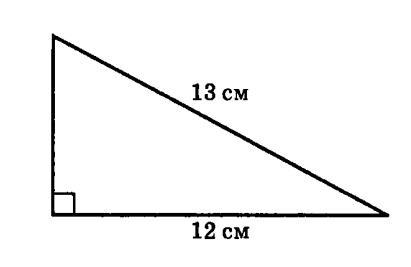
Задача№3 Найдите площадь прямоугольного треугольника, если один из его катетов равен 12 см , а гипатенуза равна 13см.
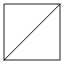
Задача №4 Сторона квадрата равна 7√2. Найдите диагональ этого квадрата.
Учитель: “Большинство из вас справились с задачами. Молодцы! Подведем итоги урока”.
VI. Подведение итогов урока. Выставление оценок. Контроль усвоения, обсуждение допущенных ошибок и их коррекция.
- Каким еще знания, кроме Т. Пифагора вам пришлось использовать при решении практических задач (высказывания учащихся).
-Что вызвало наибольшие затруднения?
- Таким образом, вы еще раз убедились, что все знания, приобретаемые на уроках, вам обязательно пригодятся.
VII. Домашнее задание. Параграф 55, 56 №490(б)
VIII. Рефлексия. Сегодня все активно работали на уроке и получат оценки после проверки ваших групповых работ.
- Я узнал, что ………………………………...
- Мне понравилось на уроке ………………..
- Было интересно……..………………………
- Сегодня я работал …………………………
- Я удивился …………………………………
- Я запомнил ………………………………….
6









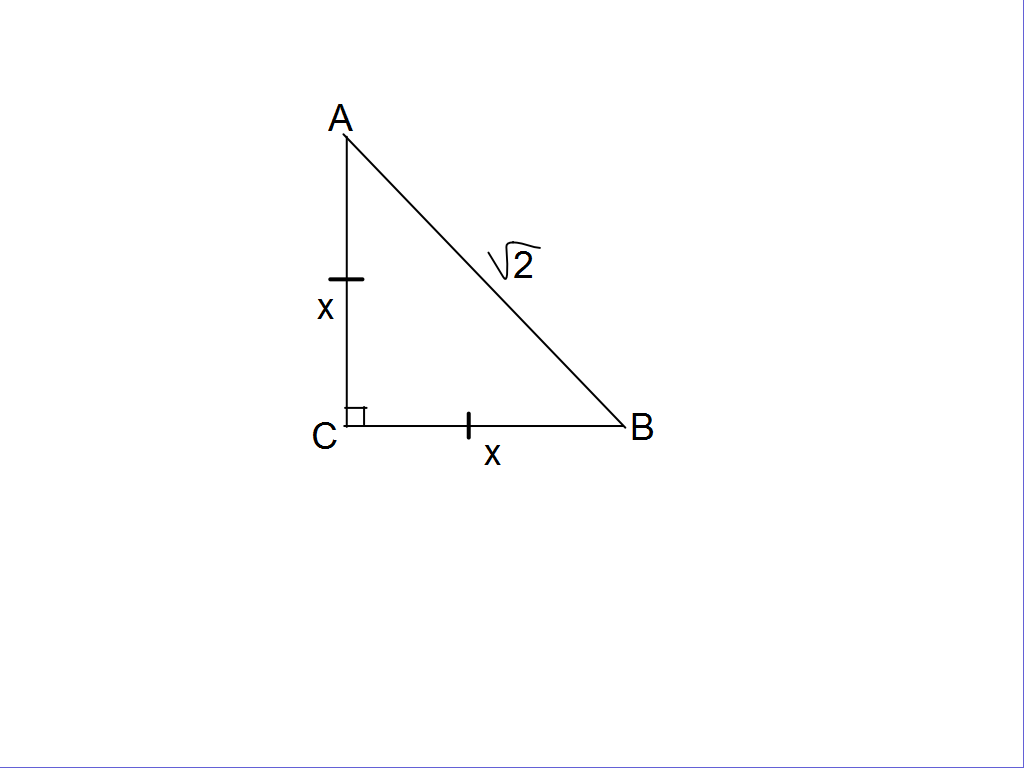





 адача №1
адача №1 Задача о бамбуке из древнекитайского трактата «Гоу - гу»
Задача о бамбуке из древнекитайского трактата «Гоу - гу» ад озером тихим
ад озером тихим адача №4
адача №4 адача №5
адача №5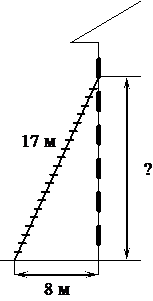 читель: “А теперь каждый попробует самостоятельно решить следующие задачи. Откуда я их взяла? Ни для кого не секрет, что в следующем году вы будете сдавать экзамен по математике в форме ГИА. И наверняка вам уже известно, что задания там будут не только по алгебре, но также и по геометрии. Так вот. Попробуйте решить некоторые из этих задач, которые я взяла из сборника по подготовке к ОГЭ по математике”. На интерактивной доске последовательно появляются три задачи.
читель: “А теперь каждый попробует самостоятельно решить следующие задачи. Откуда я их взяла? Ни для кого не секрет, что в следующем году вы будете сдавать экзамен по математике в форме ГИА. И наверняка вам уже известно, что задания там будут не только по алгебре, но также и по геометрии. Так вот. Попробуйте решить некоторые из этих задач, которые я взяла из сборника по подготовке к ОГЭ по математике”. На интерактивной доске последовательно появляются три задачи. адача№1. Пожарную лестницу длиной 17 м приставили к окну шестого этажа дома. Нижний конец лестницы отстоит от стены на 8 м. На какой высоте расположено окно? Ответ дайте в метрах
адача№1. Пожарную лестницу длиной 17 м приставили к окну шестого этажа дома. Нижний конец лестницы отстоит от стены на 8 м. На какой высоте расположено окно? Ответ дайте в метрах










