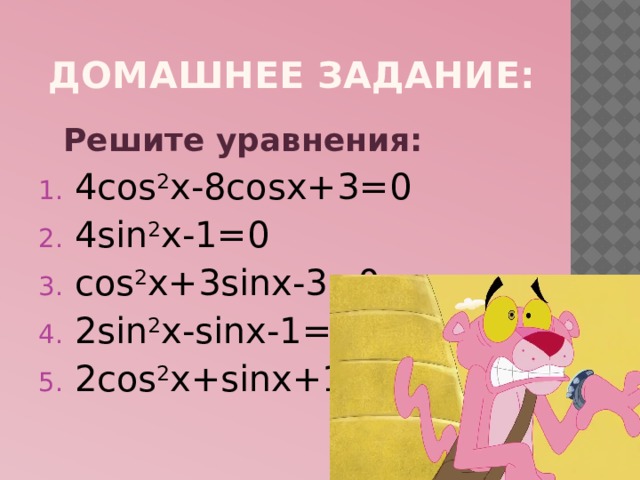Просмотр содержимого документа
«Тригонометрические уравнения, приводимые к квадратным»

Тригонометрические уравнения, приводимые к квадратным
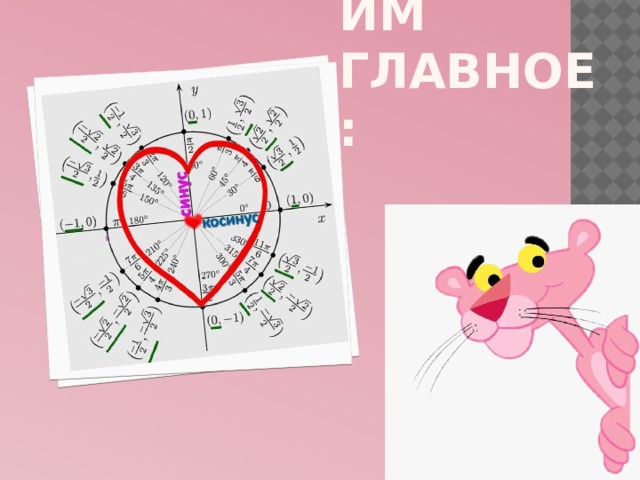
Вспомним главное:

Общие формулы для решения уравнений:
x=arctga+πn, nЄZ
а - любое
x=arcctga+πn, nЄZ
а - любое
х=±arccos a+2πn, nϵz
-1 1
x=(-1) n arcsina+πn, nϵz
-1 1

Тригонометрические уравнения, сводящиеся к квадратным Отличительные признаки таких уравнений:
- В уравнении присутствуют тригонометрические функции от одного аргумента или они легко сводятся к одному аргументу
6sin² x + 5 sin x - 7 = 0
6sin² x + 5 cos2x - 7 = 0
- В уравнении присутствует только одна тригонометрическая функция или все функции можно свести к одной
6cos² x + 5 sin x -7 = 0

А л г о р и т м р е ш е н и я
- Необходимо выразить одну тригонометрическую функцию через другую;
- Ввести обозначение (например, sin x = y );
- Решить полученное квадратное уравнение;
- Вернуться к прежней переменной;
- Подставляется значение обозначенной величины, и решается тригонометрическое уравнение.

Пример 1
D=b 2 -4ac,
х 1,2 =(-b±√D)/2а
x=(-1) n arcsina+πn, nЄZ
3sin 2 x-5sinx-2=0
Решение:
1) Пусть sinx=у, тогда
3у 2 -5у-2=0
Находим корни квадратного уровнения по формулам
2) Вернемся к прежней переменной, т.к sinx=у , то
sinx=2 -нет корней
sinx=-1/3
x=(-1) n arcsina+πn, nЄZ
x=(-1) n arcsin(-1/3)+πn, nЄZ
x=(-1) n+1 arcsin1/3+πn, nЄZ
Ответ: x=(-1) n+1 arcsin1/3+πn, nЄZ

Пример 2
D=b 2 -4ac,
х1,2=(-b±√D)/2а
x=+- arccos x + 2πn, nЄZ
2 cos 2 x – 5 cos x + 2 = 0
Решение:
1 ) Пусть cos x = y, тогда уравнение имеет вид
2 у 2 – 5у + 2 = 0
Находим корни квадратного уравнения по формуле
2) Вернемся к прежней переменной, т.к cos x = y, то
cosx= 2 – нет корней cosx=1/2
x= arccos ½ + 2Пn, nЄZ
x1=П/3 + 2Пn, X=П/3 + 2Пn
x2= -arccos ½ + 2Пn, nЄZ
x2=-П/3 + 2Пn, X=П/3 + 2Пn
Ответ: x1= П/3 + 2Пn, X=П/3 + 2Пn и х2= -П/3 + 2Пn, X=П/3 + 2Пn

Пример 3
3) Вернемся к прежней переменной
2 sin² x + cos x - 1 = 0
сosx1=1 cosx2 = ½
Решение:
x=+- arccos x + 2πn, nЄZ
1) т.к cos 2 x+sin 2 x=1 , то
x1 =- arccoc 1 + 2πn, nЄZ
sin² x= 1- cos 2 x
x2 = +- arccos (- ½ )+ 2πn, nЄZ
Получаем
2(1- cos 2 x) + cos x -1=0
x1 = +- 2π/3 + 2πn, nЄZ
x2 = +- 2πn, nЄZ
2 - 2 cos 2 x + cos x -1=0
-2 cos 2 x + cos x + 1 = 0
2) Пусть cos x = у, тогда
Ответ:
-2у 2 + у + 1 = 0
x1 = +- 2π/3 + 2πn, nЄZ
x2 = +- 2πn, nЄZ
2у 2 - у - 1 = 0
У1 = 1 у2 = - ½
Домашнее задание:
Решите уравнения:
- 4cos 2 x-8cosx+3=0
- 4sin 2 x-1=0
- cos 2 x+3sinx-3=0
- 2sin 2 x-sinx-1=0
- 2cos 2 x+sinx+1=0

Домашнее задание отправлять на почту [email protected]
Просьба, все фотографии д.р добавить в один документ word/pdf, и сбросить одним файлом. Не забываем подписывать