Просмотр содержимого документа
«Уравнения - следствия»
Урок математики по технологии критического мышления.
Тема урока: Уравнения – следствия.
Цели урока:
Образовательные:
сформировать понятие уравнения-следствия;
построить алгоритм решения уравнения-следствия;
сформировать умения пользоваться алгоритмом при решении уравнения-следствия.
Развивающие:
формирование умения выделять главное, сравнивать, анализировать и делать выводы;
формирование умения формулировать познавательные задачи, планировать познавательную деятельность;
развивать качества личности – трудолюбие, аккуратность, настойчивость в достижении цели.
Воспитательные:
Содержание урока:
Вызов.
Орг. момент. Учитель настраивает на продуктивную работу на уроке.
Как правило, у школьников есть трудности восприятия информации и формулирования целей.
На стадии вызова учащимся предлагается мини-тест. На стадии рефлексии учащиеся соотносят полученную информацию с той, что была у них на стадии вызова, что дает возможность вернуться к осмыслению или выйти на новый вызов.
Мини-тест.
Поставьте знак «+», если утверждение верно, и знак «– », если оно неверно.
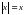 , если
, если  .
.
-1- абсцисса вершины параболы 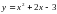 .
.
Неравенство 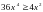 равносильно неравенству
равносильно неравенству 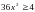 .
.
Следствием уравнения 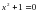 является уравнение
является уравнение 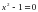 .
.
Решением совокупности 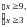 является промежуток
является промежуток 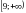 .
.
Решением системы 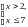 является промежуток
является промежуток 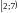 .
.
-3- наименьшее целое решение неравенства 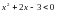 .
.
Неравенство 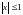 равносильно неравенству
равносильно неравенству 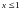 .
.
Множество значений квадратного трехчлена 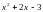 - промежуток
- промежуток 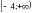 .
.
При а=2 и а =5 уравнение 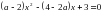 имеет единственное решение.
имеет единственное решение.
Осмысление (изучение нового материала)
Задание по тексту. Прием "Инсерт".
В процессе чтения учащиеся маркируют текст значками (" V " – уже знал; " + " – новое; “–“ – думал иначе; " ? " – не понял, есть вопросы);
Затем заполняют таблицу, количество граф которой соответствует числу значков маркировки и обсуждают записи, внесённые в таблицу.
Таким образом, обеспечивается вдумчивое, внимательное чтение, делается зримым процесс накопления информации, путь от старого знания к новому.
Прием «Толстые и тонкие вопросы»
После изучения темы учащимся предлагается сформулировать по три «тонких» и три «толстых» вопроса», связанных с пройденным материалом. Затем они опрашивают друг друга, используя таблицы «толстых» и «тонких» вопросов.
Например,
«тонкие вопросы»
Являются ли все корни исходного уравнения корнями его уравнения – следствия?
Можно ли при потенцировании уравнения потерять корни?
Число 2 является корнем второго уравнения, но посторонним для первого.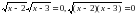
«толстые вопросы»
Дайте объяснение, почему возведение уравнения в четную степень может привести к появлению корней, посторонних для исходного уравнения.
Объясните, почему преобразование уравнения с применением формулы 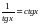 слева направо может привести к появлению посторонних корней.
слева направо может привести к появлению посторонних корней.
Объясните, почему преобразование уравнения с применением формулы 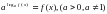 слева направо может привести к появлению посторонних корней.
слева направо может привести к появлению посторонних корней.
Тонкий вопрос предполагает однозначный краткий ответ.
Толстый вопрос предполагает ответ развернутый.
3. Выполнение теста.
1. Следствием уравнения 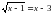 является уравнение
является уравнение 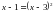
Рефлексия.
Выясняем, какие из утверждений, предложенных на стадии вызова, были верными.
Предлагается всем написать синквейн по теме урока, дается 3 – 5 минут. В результате возникает дискуссия, рождаются новые синквейны. Это даёт возможность рассуждать ученикам и критически рассматривать ту или иную тему. В дальнейшем ученики пишут синквейны не только на уроках, но и дома.
1-я строка-название синквейна – одно слово, обычно существительное, отражающее главную мысль;
2-я строка - два прилагательных, описывающих основную мысль;
3-я строка - три глагола, описывающие действия в рамках темы;
4-я строка - фраза на тему синквейна;
5-я строка - существительное, связанное с первым, отражающее сущность темы.
Подведение итогов.
Самостоятельное решение уравнений, самопроверка.
Домашнее задание.
Оценка самых активных учащихся.
Синквейн – выражение своего отношения к теме урока.






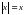 , если
, если  .
.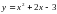 .
.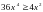 равносильно неравенству
равносильно неравенству 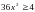 .
.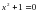 является уравнение
является уравнение 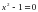 .
.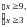 является промежуток
является промежуток 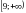 .
.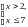 является промежуток
является промежуток 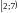 .
.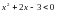 .
.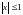 равносильно неравенству
равносильно неравенству 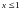 .
.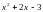 - промежуток
- промежуток 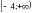 .
.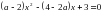 имеет единственное решение.
имеет единственное решение.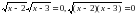
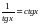 слева направо может привести к появлению посторонних корней.
слева направо может привести к появлению посторонних корней. 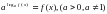 слева направо может привести к появлению посторонних корней.
слева направо может привести к появлению посторонних корней.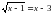 является уравнение
является уравнение 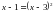
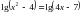 является уравнение
является уравнение 









