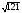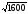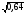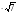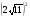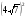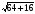Муниципальное общеобразовательное учреждение
«КУБАНСКАЯ ШКОЛА»
Урок алгебры в 8 классе
по теме «Преобразование выражений, содержащих квадратные корни»
провела учитель математики
высшей категории ВЕРЖАК С.А.
п. ШКОЛЬНОЕ, 2016
ТЕМА: Преобразование выражений, содержащих квадратные корни.
Цели урока:
повторить определение арифметического квадратного корня, свойства арифметического квадратного корня;
закрепить навыки и умения решения примеров на тождественные преобразования выражений, содержащих арифметические квадратные корни;
научить освобождаться от иррациональности в знаменателе дроби;
воспитывать навыки самоконтроля и взаимоконтроля, интерес к предмету.
Оборудование: мультимедийный проектор, интерактивная доска, оценочные листы, карточки с тестом, карточки с домашним заданием.
Ход урока:
I. Организационный момент
- Сегодня на уроке мы с вами продолжим преобразование выражений, содержащих квадратные корни. Подвести итоги сегодняшнего урока поможет оценочный лист. Подпишите свои листы и ответьте на первый вопрос «Настроение в начале урока», выбрав один из смайликов.
В математике есть нечто,
вызывающее человеческий восторг.
Ф. Хаусдорф
II. Устная работа
1) Фронтальный опрос.
Дайте определение арифметического квадратного корня. (Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а).
Перечислите свойства арифметического квадратного корня. (Арифметический квадратный корень из произведения неотрицательных множителей равен произведению корней из этих множителей. Арифметический квадратный корень из дроби, числитель которой неотрицателен, а знаменатель положителен, равен корню из числителя, делённому на корень из знаменателя).
Чему равно значение арифметического квадратного корня из х2? (|х|).
Чему равно значение арифметического квадратного корня из х2, если х≥0? хх. –х).
2) Устный счёт: Ну-ка в сторону карандаши!
Ни костяшек. Ни ручек. Ни мела.
"Устный счёт!" Мы творим это дело
Только силой ума и души.
Цифры сходятся где-то во тьме,
И глаза начинают светиться,
И кругом только умные лица.
Потому что считаем в уме!
Вычислите устно:
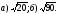
 1. Вынесите множитель из-под знака корня:
1. Вынесите множитель из-под знака корня:
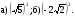 2. Внесите множитель под знак корня:
2. Внесите множитель под знак корня:
3. Возведите в квадрат:
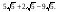 4. Приведите подобные слагаемые:
4. Приведите подобные слагаемые:
III. Диктант:
| Вариант-1
| Вариант- 2
| Ответы:
| Ответы:
|
| 
| 
| 3 | 4 |
| 
| 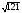
| 10 | 11 |
| 
| 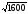
| 80 | 40 |
| 
| 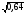
| 0,6 | 0,8 |
|  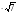
| 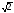 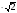
| 7 | 2 |
| 
|  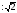 | 5 | 3 |
| 
| 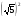
| 6 | 5 |
| 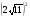
| 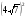
| 44 | 112 |
| 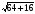
| 
| 4 | 4 |
| 
| 
| 32 | 15 |
| 
| 
| 15 | 6 |
IV.ФИЗКУЛЬТМИНУТКА
V. Историческая справка
Radix- имеет два значения: сторона и корень. Греческие математики вместо «извлечь корень» говорили «найти сторону квадрата по его данной величине (площади)»
Начиная с XIII века, итальянские и другие европейские математики обозначали корень латинским словом Radix или сокращенно R (отсюда произошёл термин «радикал»).
Немецкие математики XV в. для обозначения квадратного корня пользовались
точкой ·5
Позднее вместо точки стали ставить ромбик ¨5
¾
 Затем Ú 5 . Затем знак Ú и черту стали соединять.
Затем Ú 5 . Затем знак Ú и черту стали соединять.
VI этап. Изучение нового материала.
Если знаменатель алгебраической дроби содержит знак квадратного корня, то обычно говорят, что в знаменателе содержится иррациональность.
Ставится проблема: « Какое выражение проще вычислить:  или
или  ? Почему? (Потому, что делить на рациональное число проще, чем на иррациональное.)
? Почему? (Потому, что делить на рациональное число проще, чем на иррациональное.)
Сегодня на уроке мы и будем учиться
« Освобождению от иррациональности в знаменателе дроби». Рассмотрим это действие в следующих примерах:
а) ; б)
; б)  ; в)
; в) ; г)
; г) .
.
На какое выражение нужно умножить знаменатель дроби, чтобы корни «исчезли»? А для того чтобы дробь не изменилась, что нужно сделать? Получаем следующую запись решения.
а) =
= ;
;
б)  =
=  ;
;
в) =
=
г) =
=
Сделаем вывод.
Преобразование, при котором в знаменателе дроби исчезают корни, называют освобождением от иррациональности в знаменателе. Мы увидели два основных приема освобождения от иррациональности в знаменателе:
VII. Закрепление изученного материала: Учебник. Стр.103 № 431(а,б,ж,з), №433(а,б,в)
Освободитесь от иррациональности в знаменателе дроби:
а)  ; б)
; б) в)
в) ; г)
; г)  .
.
VIII. Тест (работа в парах)
Английский философ Герберт Спенсер говорил: «Дороги не те знания, которые откладываются в мозгу, как жир, дороги те, которые превращаются в умственные мышцы».
На этом этапе урока необходимо применить свои знания к решению упражнений в ходе выполнения теста. (тест прилагается)
Самопроверка:
Код правильных ответов: I вариант – 12312, II вариант - 32132.
IX. Домашнее задание: №431(з,и), №432, №433*(г,д,е),П.12-19 повт,
X. Итог урока:
Заполните до конца оценочный лист. Оценки за урок.
Закончить урок я хочу стихотворением великого математика Софьи Ковалевской.
Если в жизни ты хоть на мгновенье
Истину в сердце своем ощутил,
Если луч света сквозь мрак и сомненье
Ярким сияньем твой путь озарил:
Что бы в решенье твоем неизменном
Рок ни назначил тебе впереди,
Память об этом мгновенье священном
Вечно храни, как святыню в груди.
Тучи сберутся громадой нестройной,
Небо покроется черною мглой,
С ясной решимостью, с верой спокойной
Бурю ты встреть и померься с грозой.
В этом стихотворении выражено стремление к знаниям, умение преодолевать все преграды, которые встречаются на пути. А как мы сегодня с вами преодолевали преграды ? Чем мы занимались на уроке?
— Сегодня мы повторили определение и свойства арифметического квадратного корня; вынесение множителя за знак корня, внесение множителя под знак корня, формулы сокращённого умножения; ознакомились и закрепили некоторые способы преобразования выражений, содержащих квадратные корни. Расширили свой кругозор и узнали, кто впервые ввёл современный знак корня во всеобщее употребление.
Все работали плодотворно, активно и коллективно в течении урока.
Урок окончен. Всем спасибо за урок!
ЛИСТ-ОПРОСНИК
Ф.И. ученика____________________________


 1. Настроение в начале урока: а) б) в)
1. Настроение в начале урока: а) б) в)
2. Мое восприятие темы урока:
а) усвоил(а) все; б) усвоил(а) почти все; в) усвоил(а) частично, нуждаюсь в помощи.
3.Оценка за диктант :
4. Количество неправильных ответов теста: _________
5. Я работал(а) на уроке:
а) отлично; б) хорошо; в) удовлетворительно; г) неудовлетворительно.
6. Я оцениваю свою работу на ______ (поставьте оценку)
7. Я оцениваю урок на _____ (поставьте оценку)


 8. Настроение в конце урока: а) б в)
8. Настроение в конце урока: а) б в)






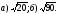
 1. Вынесите множитель из-под знака корня:
1. Вынесите множитель из-под знака корня: 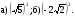 2. Внесите множитель под знак корня:
2. Внесите множитель под знак корня: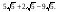 4. Приведите подобные слагаемые:
4. Приведите подобные слагаемые: