Урок геометрии " Теорема Пифагора"

«Да, путь познания не гладок.

Но знаем мы со школьных лет,

Загадок больше, чем разгадок,

И поискам предела нет!»

«Геометрия владеет

двумя сокровищами:

одно из них – это

теорема Пифагора»

Иоганн Кеплер

«Пифагоровы штаны во все стороны равны»

Современная формулировка

теоремы Пифагора

«В прямоугольном

треугольнике квадрат

гипотенузы равен

сумме квадратов катетов ».

Во времена Пифагора формулировка теоремы звучала так:

«Квадрат, построенный на гипотенузе прямо - угольного треугольника, равновелик сумме квадратов, построенных на катетах ».

Доказательство теоремы Пифагора считалось в кругах учащихся средних веков очень трудным и называлось иногда Pons Asinorum «ослиный мост» или elefuga - «бегство убогих», так как некоторые «убогие» ученики, не имевшие серьезной математической подготовки, бежали от геометрии.

Слабые ученики, заучивавшие теоремы наизусть, без понимания, и прозванные поэтому «ослами», были не в состоянии преодолеть теорему Пифагора, служившую для них вроде непреодолимого моста.

В некоторых списках «Начал» Евклида теорема Пифагора называлась теоремой Нимфы, «теорема – бабочка», по-видимому из-за сходства чертежа с бабочкой, поскольку словом «нимфа» греки называли бабочек. Нимфами греки называли еще и невест, а также некоторых богинь.

При переводе с греческого арабский переводчик, вероятно, не обратил внимания на чертеж и перевел слово «нимфа» не как «бабочка», а как «невеста». Так и появилось ласковое название знаменитой теоремы – «Теорема Невесты».

«Нимфа» - бабочка, невеста

Теорема

в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов

Дано : прямоугольный

треугольник с катетами a , b и гипотенузой c .

β

c

b

α

Док-ть : a 2 + b 2 = c 2

a

b

α

β

α

β

α

β

a

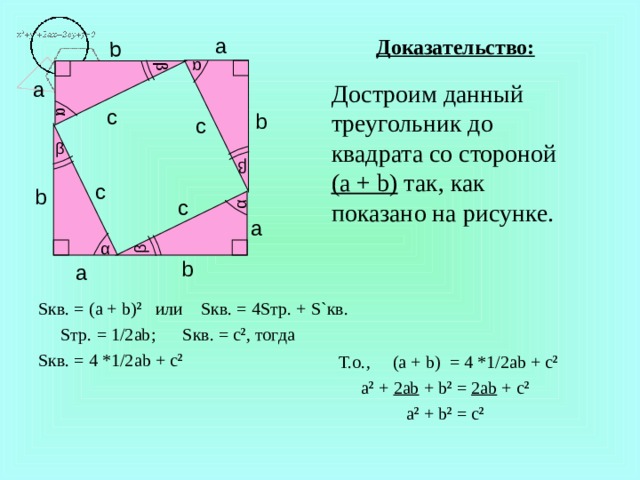
Доказательство:

a

Достроим данный треугольник до квадрата со стороной ( a + b) так, как показано на рисунке.

c

b

с

β

c

b

c

a

α

b

a

S кв. = (a + b) 2 или S кв. = 4 S тр. + S` кв.

S тр. = 1/2 ab ; S кв. = c 2 , тогда

S кв. = 4 *1/2 ab + c 2

Т.о., (a + b) = 4 *1/2 ab + c 2

a 2 + 2ab + b 2 = 2ab + c 2

a 2 + b 2 = c 2

Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах...

Дано: Δ АВС-прямоугольный , АС = а, ВС = b , АВ = с

А

S = c 2

b

S = b 2

с

Доказать: АВ 2 = АС 2 + ВС 2

a

В

С

S = a 2

РЕШЕНИЕ ЗАДАЧ

ЗАДАЧА 1

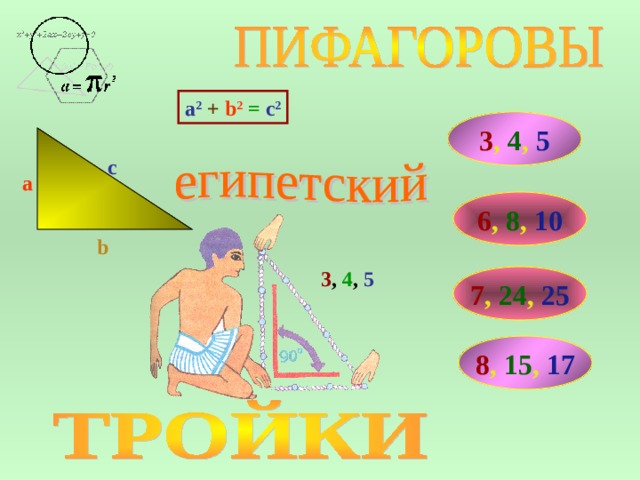
a 2 + b 2 = c 2

3 , 4 , 5

c

a

6 , 8 , 10

b

3 , 4 , 5

7 , 24 , 25

8 , 15 , 17

Делай лишь то.что в последствии не огорчит тебя и не принудит раскаиваться

Не делай никогда того, что не знаешь, но научись всему, что следует знать, и тогда ты будешь вести спокойную жизнь.

Не пренебрегай здоровьем своего тела.

Доставляй ему вовремя пищу и питьё, и упражнения, в которых он нуждается.

ВОПРОС 1

Периметр прямоугольника равен 62 см, а точка пересечения диагоналей удалена от одной из его сторон на 12 см.

Найдите длину диагонали прямоугольника

ВОПРОС 2

Периметр ромба 68 см, а одна из его диагоналей равна 30 см. Найдите длину другой диагонали

ВОПРОС 3

В треугольнике С DE CD = 15 см, DE = 13 см, CE = 14 см. Найдите высоту DM .

РЕЗУЛЬТАТ

ВСЕГО ЗАДАНИЙ ВЫПОЛНЕНО

ВЫПОЛНЕНО ВЕРНО

ПРОЦЕНТ ВЫПОЛНЕНИЯ

ОЦЕНКА

Домашнее задание:

• П.54, вопрос 8.
• Решить задачи
• № 483 (в, г),
• № 484 (в, г)