Урок обобщения и систематизации знаний по теме Теорема Пифагора

Урок обобщения и систематизации знаний по теме «Теорема Пифагора. Перпендикуляр и наклонная»

Цели урока:

Образовательная: создать условия для обобщения и систематизации теоремы Пифагора, понятия перпендикуляр и наклонная;

Развивающая: способствовать развитию способности к сопоставлению, наблюдательности, внимания, развитие способности к аналитико-синтетическому мышлению, расширение кругозора;

Воспитательная: формирование потребности в знаниях, интереса к математике.

Ход урока.

1. Организационный момент

-Чтобы спорилось нужное дело,

Чтобы в жизни не знать неудач,

В мир многоугольников отправимся смело,

В мир примеров и разных задач.

Здравствуйте, ребята! Пожелаем, друг другу удачи на уроке и вдохновения, как говорил А.С.Пушкин: «Вдохновение нужно в геометрии не меньше, чем в поэзии».

Настроение в начале урока выставляется в личной карточке.

2. Мотивация урока

Особое место в геометрии занимает прямоугольный треугольник, теорема Пифагора, соотношение между сторонами и углами прямоугольного треугольника. На протяжении нескольких уроков мы с вами изучали этот материал и сегодня урок посвящен теореме Пифагора, целью которого является обобщение полученных знаний по данной теме. Этот урок пройдет в форме конференции. К вопросу обобщения мы подойдем многосторонне, как теоретики, историки, лирики и практики.

3. Актуализация опорных знаний. Проверка д/з.

Итак, теоретики – вперед!

Устный опрос:

1) Что такое треугольники?

2) Основные элементы, определяющие треугольник?

3) Какие бывают треугольники в зависимости от сторон?

4) Какие бывают треугольники в зависимости от углов?

5) Что такое катет?

6) Что такое гипотенуза?

7) Чему равен катет, лежащий против угла в 30 градусов?

8) Сформулируйте теорему Пифагора

9) Дать определение синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника

Устное решение задач по рисункам:

Из истории (выступление ученика, демонстрация слайдов презентации, подготовленной учащимися)

Теорема Пифагора издавна применялась в разных областях науки и техники, в практической жизни.

Доказательство теоремы Пифагора считалось в кругах учащихся средних веков очень трудным и называлось иногда «ослиным мостом» или «бегством убогих», т.е. некоторые слабые ученики бежали от геометрии, не пытаясь понять, а зазубривая доказательство. «Ослиный мост» - непроходимый мост. А посему возникали, своего рода карикатуры, сопровождающие чертежи к доказательству теоремы

4. Решение задач по теме «Теорема Пифагора. Перпендикуляр и наклонная»

А теперь проверим, как хорошо вы умеете применять теоретические знания при решении задач по данной теме.

Задача 1.(работа у доски)

Для крепления мачты нужно установить 4 троса. Один конец каждого троса должен крепиться на высоте 12 м, другой на земле на расстоянии 5 м от мачты.

Хватит ли 50 м троса для крепления мачты?

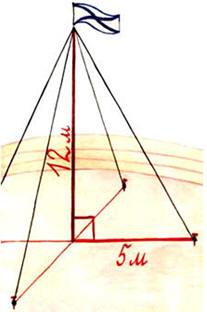
Задача из старинного китайского трактата.(работа в парах)

В центре квадратного пруда, имеющего 10 футов в длину и ширину, растет камыш, возвышающийся на 1 фут над поверхностью воды. Если его пригнуть к берегу, к середине стороны пруда, то он достигнет своей верхушкой берега. Какова глубина пруда?

Решить № 858(1)- самостоятельно, предварительно обсудив ход решение в группах, 866(1), 914- у доски.

5. Лирическая пауза.

Сохранилось древнее предание, что в честь своего открытия Пифагор принес в жертву богам быка, по другим свидетельствам – даже сто быков. Многие известные мыслители и писатели прошлого обращались к этой замечательной теореме и посвятили ей свои строки. Слово предоставляем лирикам. В их лице мы услышим выступление ученицы …, которая прочтет сонет Шамиссо.

6. Самостоятельная работа.

Для выявления степени усвоения изученного материала проведем самостоятельную работу.

(учащиеся получают индивидуальные карточки с заданием различного уровня сложности)

Уровень А.

Карточка 1.

1. Выяснить является ли треугольник прямоугольным, если его стороны выражаются числами 11, 9, 13.

2. В прямоугольном треугольнике один из катетов равен 7 см, а гипотенуза 9 см. Найти другой катет.

Карточка 2.

1. Выяснить является ли треугольник прямоугольным, если его стороны выражаются числами 10, 24, 26.

2. Найти гипотенузу прямоугольного треугольника, если его катеты равны 5м и 6м.

Уровень В.

Карточка 1.

1. Боковая сторона равнобедренного треугольника равна 17 см, а основание равно 16 см. Найдите высоту, проведенную к основанию.

2. Является ли треугольник прямоугольным, если длины его сторон равны 9, 12 и 15.

Карточка 2.

1. Найти высоту равностороннего треугольника, если его сторона равна 6м.

2. Является ли треугольник прямоугольным, если его стороны равны 7, 14, 15.

Уровень С.

Карточка 1.

1. В прямоугольной трапеции основания равны 22 см и 6 см, а большая боковая сторона – 20 см. Найти площадь трапеции.

2. Найдите сторону ромба, если его диагонали равны 10 см и 24 см.

Карточка 2.

1. Боковые стороны прямоугольной трапеции равны 7 см и 25 см, а меньшее основание – 2см. Найти площадь трапеции.

2. Найти диагональ ромба, если одна из диагоналей равна 12 см, а сторона – 10 см.

(по истечении времени карточки должны быть сданы, результаты - на следующем уроке)

7.Итоги урока. Рефлексия. Д/з.

Повторить п. 20, 21. Решить № 858(2), 866(2), 908.

Задача о лотосе из сочинения Бхаскары (12 века)

На стебле с полфунта над озером тихим,

Рос лотоса цвет.

Он рос одиноко. И ветер порывом

Отнес его в сторону. Нет

Больше цветка над водой.

Нашел же рыбак его ранней весной

В двух футах от места, где рос:

Как озера вода здесь глубока?

Причина популярности теоремы Пифагора триедина: это простота — красота — значимость. В самом деле, теорема Пифагора проста, но не очевидна. Это сочетание двух противоречивых начал и придает ей особую притягательную силу, делает ее красивой. Но, кроме того, теорема Пифагора имеет огромное значение: она применяется в геометрии буквально на каждом шагу, и тот факт, что существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.), свидетельствует о гигантском числе ее конкретных реализаций.

• Возможно ли было решение задач, которые мы рассматривали на уроке, без знания теоремы Пифагора?

• О чём надо помнить, применяя теорему Пифагора?

• Достигли ли мы цели урока?

• Что вам понравилось на этом уроке?

Составьте, пожалуйста «Сенкан»-один из жанров поэзии

• 1 строчка – теорема Пифагора;

• 2 строчка – 2 прилагательных;

• 3 строчка – 3 глагола;

• 4 строчка – предложение, выражающее личное отношение.

Затем учитель объявляет, комментируя, оценки за урок. Благодарит всех за работу.