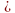Предмет: математика
Класс: 6
Учебник (УМК): Математика: 6 класс: учебник для учащихся общеобразовательных организаций/ А.Г.Мерзляк, В.Б.Полонский, м.С.Якир. – 3-е изд. –М. :Вентана-Граф, 2018. –304с.
Тема урoка: Решение задач с помощью уравнений
Тип урока: урок закрепления знаний и навыков
Цель урока: закрепление навыков решения задач на составление уравнений
Задачи урока
-
Закрепить навыки составления уравнений по условию текстовой задачи.
-
Закрепить навыки решения уравнений.
-
Снять монотонность урока и перегрузку учащихся, повысить интерес к математике, используя для этого различные методы проведения урока на разных его этапах.
Место урока в системе уроков: данный урок является третьим занятием по теме «Решение задач с помощью уравнений»
Формы организации деятельности: индивидуальная, фронтальная, групповая.
Оборудование: мультимедийный проектор, презентация, карточки с заданиями
План урока
-
Организационный момент: приветствие
-
Постановка цели урока. Слайд1,2,3
-
Устная работа
-
Актуализация знаний по теме «Решение уравнений». Блиц-опрос на повторение изученного материала с помощью системы интерактивного голосования vote. Слайд 4, переход по гиперссылке на опрос.
-
проведение опроса по теоретическому материалу
-
выявление учащихся наиболее хорошо справившихся с заданием.
-
Решение задач с помощью уравнения. Слайд4, переход по гиперссылке «Решение задач»
-
Физминутка. Слайд4, переход по гиперссылке «Физминутка»
-
Работа по группам. Выступление представителей групп с решением задач. Слайды 26,27,28,29
-
Подведение итогов урока, постановка домашнего задания, рефлексия с помощью быстрого голосования mimio vote, выявление наиболее активно работающих учеников на уроке. Слайд4, переход по гиперссылке «Подведем итоги»
Ход урока
-
Организационный этап
Приветствие учащихся
-
Мотивация
Наш урок мне хочется начать со слов великого ученого с мировым именем Альберта Эйнштейна. Ребята, обратите внимание на его высказывание:
«Мне приходится делить время между политикой и уравнениями. Однако, уравнения, по-моему, гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно»
Как вы думаете, о чем сегодня пойдет речь на уроке? О чём будем говорить?
(ответы учащихся, предположительно – «об уравнениях»)
Для чего же нужны уравнения? (Ответы учащихся)
Вы уже умеете решать различные виды уравнений и задачи с помощью уравнений, и сегодня на уроке мы с вами продолжим решать задачи с помощью уравнений.
3. Актуализация знаний
Какие бы сложные и интересные темы не изучали по математике, но без арифметики нам не обойтись. Давайте проверим, как у нас обстоят дела с устным счетом.
Вы знаете, что 12 апреля отмечалась юбилейная дата (какая?) Да 60 лет тому назад впервые в мире на специальном летательном корабле поднялся в космос наш соотечественник Ю.А. Гагарин (Юрий Алексеевич Гагарин). Он стал самым известным человеком на планете.
Как назывался первый космический корабль?
Чтобы ответить на этот вопрос мы должны прочитать шифровку. Ответ примера соответствует определённой букве.
| К | Ю | О | З | В | А | С | М | Т | Е |
| -40 | 5 | -4 | 35 | -10 | 60 | 100 | 10 | 200 | 40 |
Итак, мы узнали, что космический корабль назывался «Восток».
А чтобы узнать, сколько же длился этот полёт необходимо решить два уравнения и сложить их корни. Каждой группе я даю по 1 уравнению
0,4с+0,5с-0,8с =10,4 (с=104) и -3,24с+2,2с+1,08с = 0,16 (с=4)
Ученики называют корни уравнений, а я на доске нахожу сумму. Итак,
Этот полет длился 108 минут. За 108 минут корабль-спутник с первым в мире космонавтом облетел земной шар и благополучно вернулся на Землю вблизи деревни Смеловка Энгельсского района Саратовской области (перевести в часы 1ч. 48мин)
А сейчас проведём небольшой блиц-опрос, если согласны, то поднимайте зелёные карточки, а если нет - красные
1)Корни уравнения изменятся, если обе части уравнения умножить на одно и тоже число.
2) Корни уравнения не изменятся, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом знаки.
3) Если перед скобкой стоит знак "минус", то нужно раскрыть скобки, сохранив знаки слагаемых.
4) На нуль делить можно
5) Чтобы сложить подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть.
6) Если перед скобками стоит знак "плюс", то можно опустить скобки, сохранив знаки слагаемых.
7) Произведение может быть равно нулю, когда хотя бы один из множителей равен нулю ответ 0100111
-
Применение знаний и умений
Мы уже не первый урок решаем задачи с помощью уравнений и знаем алгоритм их решения. Сейчас каждой группе предлагаю правильно расставить шаги алгоритма
Приложение 1. Задание для составления алгоритма «Решение задач с помощью уравнений»
В каком порядке нужно выполнить следующие действия, чтобы решить задачу?
| Порядок | Действия |
|
| Выразить другие неизвестные величины через ту, которую обозначили буквой |
|
| Найти оставшиеся неизвестные величины |
|
| Решить уравнение |
|
| Обозначить буквой неизвестную величину |
|
| Составить уравнение |
|
| Проверить, удовлетворяет ли корень уравнения условию задачи |
На выполнение минута. Кто готов, поднимаем красную карточку.
Проверяем, читаем.
Далее решаем задачи по группам, один уч-ся записывает задание на доске (кто первый)
Задача №1 (на слайде)
Сейчас отцу 32 года, а сыну 5 лет, через сколько лет отец будет старше сына ровно в два раза?
| Отец | 32 | 32+х | В 2 раза |
| Сын | 5 | 5+х |
|
Составим уравнение: 32+х=2(5+х)
Решаем уравнение:
32+х=10+2х;
-2х+х=10-32;
-Х=-22.
Х=22
Ответ: через 22 года возраст отца будет в 2 раза больше возраста сына.
Задача 2 Решаем в группах самостоятельно. Условие задачи запишем в таблицу
| продукты | цена | количество | стоимость |
| Конфеты |
|
|
|
| Печенье |
|
|
|
| Зефир |
|
|
|
Мама на день рождения сына в школу купила конфеты, печенье и зефир. Зефир на 20 р., а конфеты на 50 р. стоят дороже, чем печенье. Определите цену за 1кг каждого продукта, если за 2 кг конфет, 3 кг печенья и 1 кг зефира было уплачено 1320 р.?
2(х+50)+3х+х+20 = 1320
2х+3х+х = 1320-100-20
6х = 1200
Х=200
Ответ: Печенье – 200 р; зефир – 220 р; конфеты – 250 р.
Представитель группы, первой решивший задачу, выходит к доске, составляет уравнение и решает.
Если не справились, то я объясняю с помощью учеников.
Физминутка (глаза, шея, плечи)
4. Групповая самостоятельная работа (15-18 мин)
У каждой группы по 6 одинаковых задач. Решайте задачи на листочках и передавайте мне для проверки.
№1 В двух ящиках 108 кг яблок. В первом ящике в 5 раз больше яблок, чем во втором. Сколько килограммов яблок в каждом ящике?
№2 На первом катере в 2 раза больше людей, чем на втором. Когда на ближайшей пристани с первого катера сошли 98 человек, а со второго-16 человек, то на обоих катерах людей стало поровну. Сколько человек было на каждом катере первоначально?
№ 3 В первом бидоне в три раза больше молока, чем во втором. Если из первого перелить 20 л во второй, то молока в бидонах будет поровну. Сколько молока в каждом бидоне?
№ 4 В первой колбе было 47 г воды, а во второй – 75 г воды. Сколько грамм воды надо перелить в первую колбу, чтобы в обеих колбах воды стало поровну?
№ 5 На первой полке было 33 книги, а на другой – 21 книга. Сколько книг нужно переставить с первой полки на вторую, чтобы книг стало поровну?
№ 6 На одном складе было в 2 раза больше телевизоров, чем на другом. После того, как с первого склада взяли 20 телевизоров, а на другой привезли 14, телевизоров на обоих складах стало поровну. Сколько телевизоров было на каждом складе первоначально?
-
Подведение итогов урока.
В чем состоит искусство решения задач?
(составить уравнение, перевести задачу на математический язык)
Составление математической модели. С этим и возникает больше затруднений, так как формулировки задач бывают разные, а математических знаков, чтобы их перевести на математический язык не так много.
6. Домашнее задание Запишем домашнее задание (слайд)
7. Рефлексия.
Оценка своей работы на уроке : все получилось, были затруднения, ничего не получилось. (голосуем карточками)
Решали мы задачи с уравнением.
Безошибочно их надо всем решать.
В жизни вы, конечно, все их встретите.
Остается вам успехов пожелать.
Приложение 1.
2:(-0,2)
-3,2:0,8
-7:(-0,07)
28:0,14
2,4:(-0,6)
-0,8:0,02
Запишите около каждого ответа соответствующую букву
| К | Ю | О | З | В | А | С | М | Т | Е |
| -40 | 5 | -4 | 35 | -10 | 60 | 100 | 10 | 200 | 40 |
Приложение 2.
0,4с+0,5с-0,8с =10,4 (с=104) и -3,24с+2,2с+1,08с = 0,16 (с=4)
Приложение 3.
Задание для составления алгоритма «Решение задач с помощью уравнений»
В каком порядке нужно выполнить следующие действия, чтобы решить задачу?
| Порядок | Действия |
|
| Выразить другие неизвестные величины через ту, которую обозначили буквой |
|
| Найти оставшиеся неизвестные величины |
|
| Решить уравнение |
|
| Обозначить буквой неизвестную величину |
|
| Составить уравнение |
|
| Проверить, удовлетворяет ли корень уравнения условию задачи |
Приложение 4.
Задача 1 Сейчас отцу 32 года, а сыну 5 лет, через сколько лет отец будет старше сына ровно в два раза?
Приложение 5.
Задача 2 Мама на день рождения сына в школу купила конфеты, печенье и зефир. Зефир на 20 р., а конфеты на 50 р. стоят дороже, чем печенье. Определите цену за 1кг каждого продукта, если за 2 кг конфет, 3 кг печенья и 1 кг зефира было уплачено 1320 р.?
| продукты | цена | количество | стоимость |
| Конфеты |
|
|
|
| Печенье |
|
|
|
| Зефир |
|
|
|
№1 В двух ящиках 108 кг яблок. В первом ящике в 5 раз больше яблок, чем во втором. Сколько килограммов яблок в каждом ящике?
№2 На первом катере в 2 раза больше людей, чем на втором. Когда на ближайшей пристани с первого катера сошли 98 человек, а со второго-16 человек, то на обоих катерах людей стало поровну. Сколько человек было на каждом катере первоначально?
№ 3 В первом бидоне в три раза больше молока, чем во втором. Если из первого перелить 20 л во второй, то молока в бидонах будет поровну. Сколько молока в каждом бидоне?
|
| Было | перелить | Стало |
| I бидон |
|
|
|
| II бидон |
|
|
|
№ 4 В первой колбе было 47 г воды, а во второй – 75 г воды. Сколько грамм воды надо перелить в первую колбу, чтобы в обеих колбах воды стало поровну?
Пусть x г воды перелили.
|
| Было | перелить | Стало |
| I колба |
|
|
|
| II колба |
|
|
|
№ 5 На первой полке было 33 книги, а на другой – 21 книга. Сколько книг нужно переставить с первой полки на вторую, чтобы книг стало поровну?
№ 6 На одном складе было в 2 раза больше телевизоров, чем на другом. После того, как с первого склада взяли 20 телевизоров, а на другой привезли 14, телевизоров на обоих складах стало поровну. Сколько телевизоров было на каждом складе первоначально?