Урок- презентация по теме "Движения" 9 класс

У рок по теме: «Движения».

Работу выполнила : Ткачук Т.П.

Учитель 1 категории,

МБОУ СОШ №5 г. Серпухов

Цели и задачи урока: 1.Ввести понятия отображения плоскости на себя и движения. 2.Рассмотреть свойства движений. 3. Вспомнить осевую и центральную симметрии. 4.Познакомить учащихся с параллельным переносом и поворотом. 5.Совершенствовать навыки решения задач на построение фигур при осевой и центральной симметрии.

I . Введём понятия отображения плоскости на себя и движение.

II. Свойства движений: 1.При движении сохраняются расстояния между точками. 2.Расстояние между точками равно расстоянию между симметричными им точками. 3. При движении отрезок отображается на отрезок, а треугольник на равный ему треугольник.

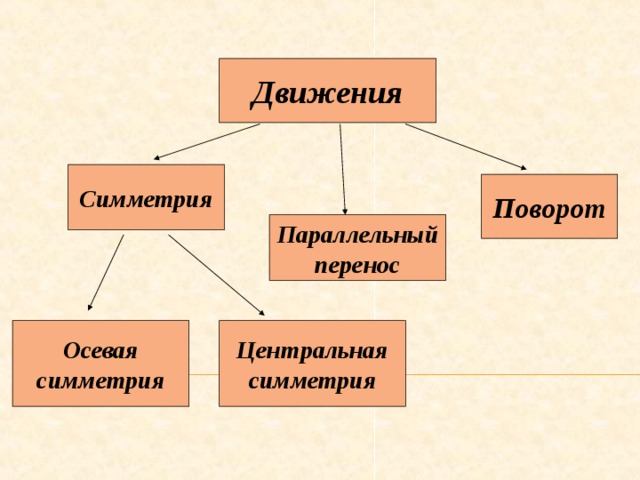
Движения

Симметрия

Поворот

Параллельный

перенос

Осевая

симметрия

Центральная

симметрия

Герман Клаус Гуго Вейль

СИММЕТРИЯ....ЕСТЬ ИДЕЯ, С ПОМОЩЬЮ КОТОРОЙ ЧЕЛОВЕК ВЕКАМИ ПЫТАЛСЯ ОБЪЯСНИТЬ И СОЗДАТЬ ПОРЯДОК, КРАСОТУ И СОВЕРШЕНСТВО.

Осевая симметрия

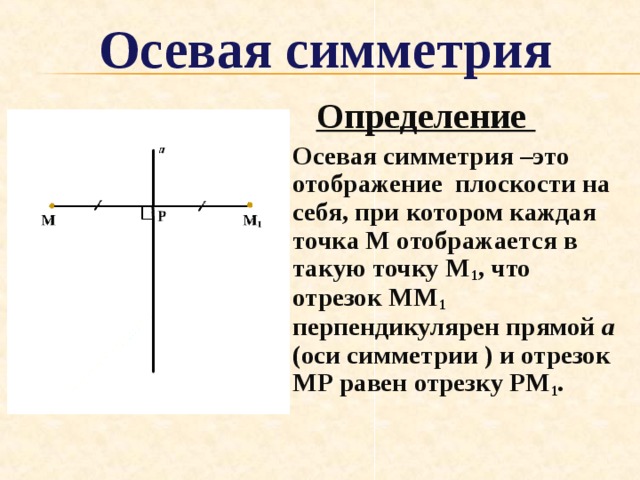
Определение

Осевая симметрия –это отображение плоскости на себя, при котором каждая точка М отображается в такую точку М 1 , что отрезок ММ 1 перпендикулярен прямой а (оси симметрии ) и отрезок МР равен отрезку РМ 1 .

Построение

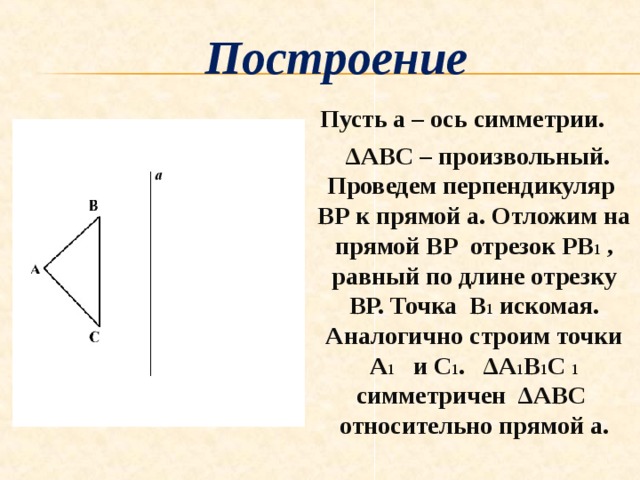
Пусть а – ось симметрии.

∆ АВС – произвольный. Проведем перпендикуляр ВР к прямой а. Отложим на прямой ВР отрезок РВ 1 , равный по длине отрезку ВР. Точка В 1 искомая. Аналогично строим точки А 1 и С 1 . ∆А 1 В 1 С 1 симметричен ∆АВС относительно прямой а.

Задачи:

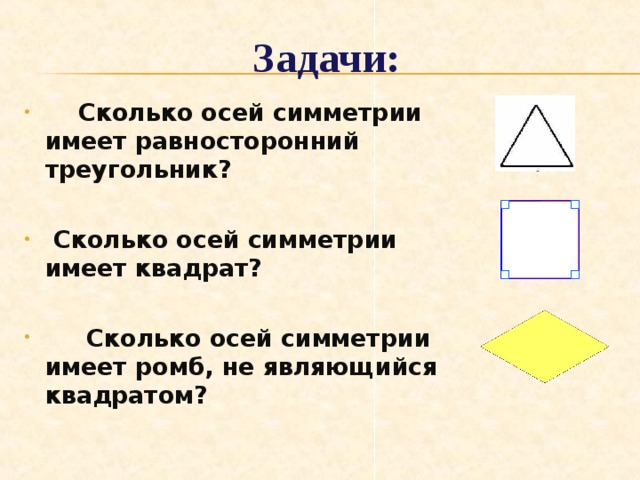
• Сколько осей симметрии имеет равносторонний треугольник?

• Сколько осей симметрии имеет квадрат?

• Сколько осей симметрии имеет ромб, не являющийся квадратом?

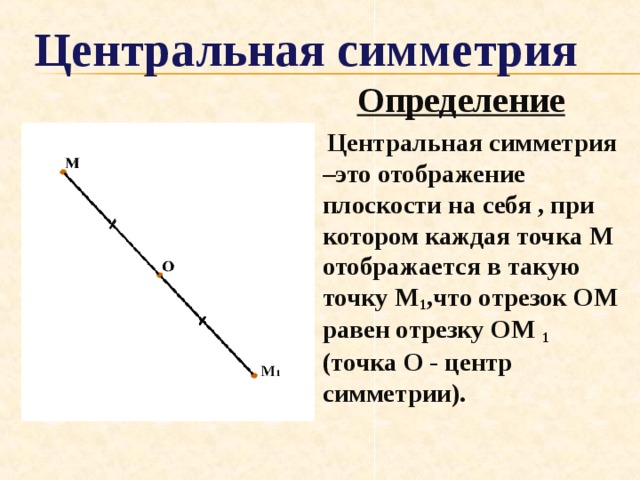
Центральная симметрия

Определение

Центральная симметрия –это отображение плоскости на себя , при котором каждая точка М отображается в такую точку М 1 ,что отрезок ОМ равен отрезку ОМ 1 (точка О - центр симметрии).

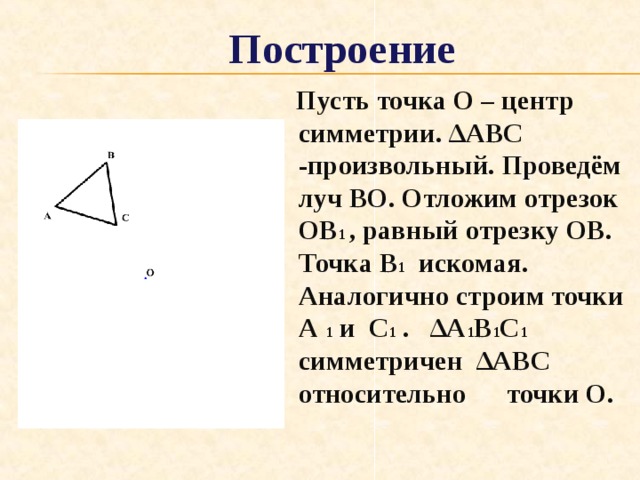
Построение

Пусть точка О – центр симметрии. ∆АВС -произвольный. Проведём луч ВО. Отложим отрезок ОВ 1 , равный отрезку ОВ. Точка В 1 искомая. Аналогично строим точки А 1 и С 1 . ∆А 1 В 1 С 1 симметричен ∆АВС относительно точки О.

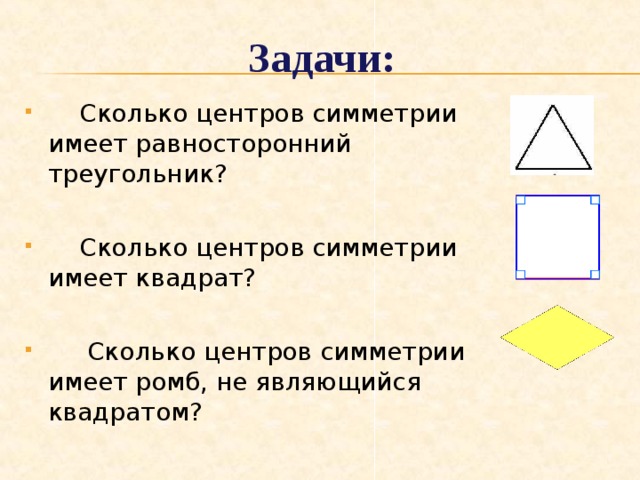
Задачи:

• Сколько центров симметрии имеет равносторонний треугольник?

• Сколько центров симметрии имеет квадрат?

• Сколько центров симметрии имеет ромб, не являющийся квадратом?

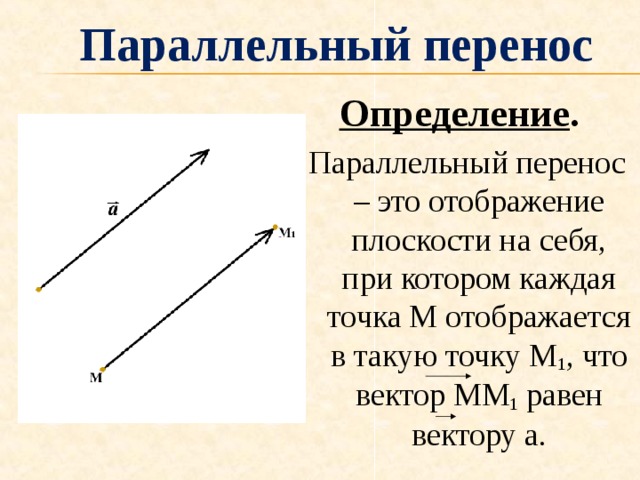
Параллельный перенос

Определение .

Параллельный перенос – это отображение плоскости на себя, при котором каждая точка М отображается в такую точку М 1 , что вектор ММ 1 равен вектору а.

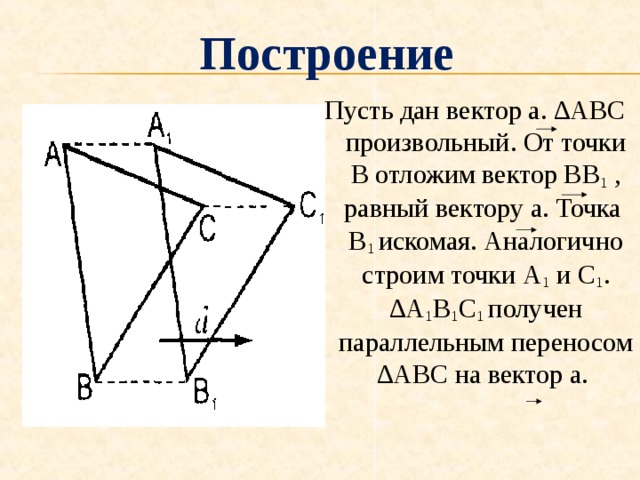
Построение

Пусть дан вектор а. ∆АВС произвольный. От точки В отложим вектор ВВ 1 , равный вектору а. Точка В 1 искомая. Аналогично строим точки А 1 и С 1 . ∆А 1 В 1 С 1 получен параллельным переносом ∆АВС на вектор а.

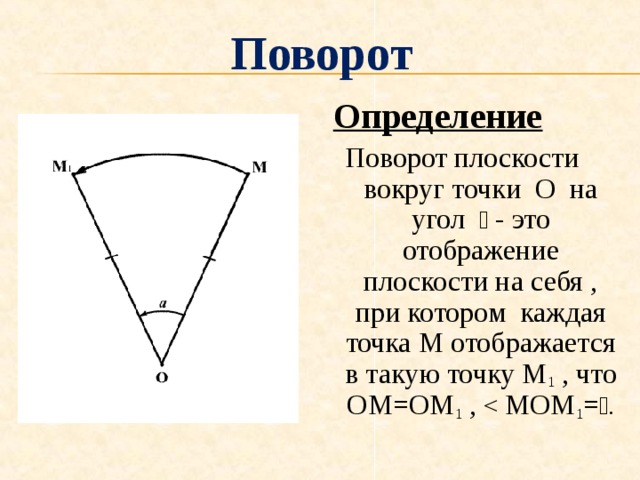
Поворот

Определение

Поворот плоскости вокруг точки О на угол  - это отображение плоскости на себя , при котором каждая точка М отображается в такую точку М 1 , что ОМ=ОМ 1 ,

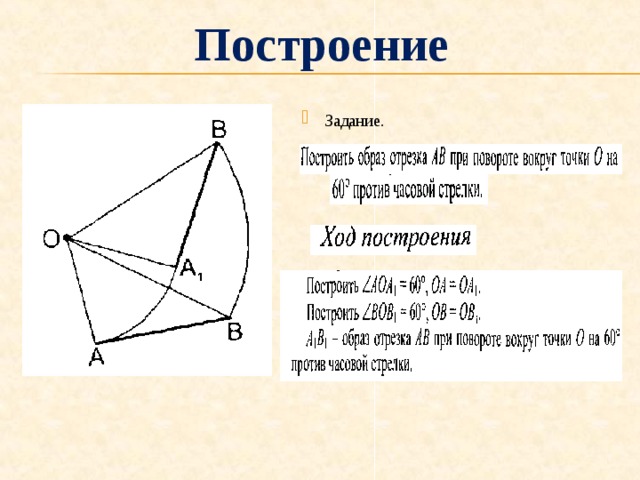
Построение

• Задание.

Симметрия в природе

Бабочка

Медуза

Морская звезда

Ель

Зеркальная симметрия

Лист

Лучевая симметрия

Итог урока:

• было трудно…
• я выполнял задания…
• я понял, что…
• теперь я могу…
• я научился…
• у меня получилось …
• я смог…
• меня удивило…
• мне захотелось…

Домашнее задание.

1. Сделать рисунки симметричных фигур (растения, животные и другие объекты).

2. Изготовить модели фигур, имеющие несколько осей и плоскостей симметрии (геометрия, химия)

3. Решить задачи по геометрии №1157, №1158, №1160

Использование ИКТ на уроке нужно для:

1. Привлечения внимания.

2.Дифференциации обучения.

3.Усиления мотивации к обучению.

4.Улучшения качества обучения и воспитания, что повышает информационную культуру у учащихся.

Уроки с использованием ИКТ помогают решить следующие дидактические задачи:

• систематизировать усвоенные знания;
• сформировать навыки самоконтроля;
• усвоить базовые знания по предмету;
• сформировать мотивацию к учению;
• оказать учебно-методическую помощь учащимся в самостоятельной работе
• над учебным материалом.

Компьютерные технологии позволяют:

• Выиграть время для более интенсивного обучения.
• Сделать урок интересным, разнообразным и наглядным.
• Вовлечь всех детей в учебный процесс.
• Вводить новое через компьютерные технологии.
• Развивать творчество учащихся.

• Увеличивать самостоятельность школьников. Больше внимания уделяется потребности личности в саморазвитии . Активизируется познавательная деятельность учащихся на уроках и в послеурочное время. Возможна реализация опережающего обучения, в том числе и для учащихся с низким и средним уровнем обученности. Максимально учитываются не только фактические знания, но и всесторонне оцениваются способности, умение работать в коллективе, индивидуальность мышления
• Увеличивать самостоятельность школьников. Больше внимания уделяется потребности личности в саморазвитии . Активизируется познавательная деятельность учащихся на уроках и в послеурочное время. Возможна реализация опережающего обучения, в том числе и для учащихся с низким и средним уровнем обученности. Максимально учитываются не только фактические знания, но и всесторонне оцениваются способности, умение работать в коллективе, индивидуальность мышления
• Увеличивать самостоятельность школьников. Больше внимания уделяется потребности личности в саморазвитии . Активизируется познавательная деятельность учащихся на уроках и в послеурочное время. Возможна реализация опережающего обучения, в том числе и для учащихся с низким и средним уровнем обученности. Максимально учитываются не только фактические знания, но и всесторонне оцениваются способности, умение работать в коллективе, индивидуальность мышления
• Увеличивать самостоятельность школьников. Больше внимания уделяется потребности личности в саморазвитии . Активизируется познавательная деятельность учащихся на уроках и в послеурочное время. Возможна реализация опережающего обучения, в том числе и для учащихся с низким и средним уровнем обученности. Максимально учитываются не только фактические знания, но и всесторонне оцениваются способности, умение работать в коллективе, индивидуальность мышления
• Увеличивать самостоятельность школьников.
• Больше внимания уделяется потребности личности в саморазвитии .
• Активизируется познавательная деятельность учащихся на уроках и в послеурочное время.
• Возможна реализация опережающего обучения, в том числе и для учащихся с низким и средним уровнем обученности.
• Максимально учитываются не только фактические знания, но и всесторонне оцениваются способности, умение работать в коллективе, индивидуальность мышления

Спасибо за внимание!

МЕЧТА

ИСПОЛНЕНИЕ