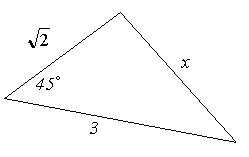Урок теорема косинусов 9 кл

Учитель : Калинина Евгения Геннадьевна, МОУ «СОШ №33» Г. Саранск

• Цели урока: Образовательные:

• Доказать теорему косинусов и показать ее применение при решении задач

• Способствовать усвоению всеми учащимися стандартного минимума по теме;

• Формировать  и совершенствовать  надпредметные умения обобщать путем  сравнения,   постановки и решения проблем, оперированием  уже знакомыми геометрическими понятиями и фактами, рассуждением  по аналогии;

• Развивающие:

•  развивать тригонометрический аппарат как средство решения геометрических задач;

• развивать психические  свойства: память, вербальную и образную, произвольное внимание, воображение.

• Воспитывающие: воспитывать чувство коллективизма.

Ход урока

1. Новый материал

Историческая справка: Впервые теорема косинусов была доказана учёным –математиком аль-Бируни (973-1048 г.г.). С помощью данной теоремы и теоремы синусов , можно будет полностью решить задачу: «Решить треугольник», т.е. как зная одни из основных элементов треугольника (их 6: 3 угла и 3 стороны), найти другие.

Теорема: Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.

Дано:

Треугольник АВС.

Доказать:

1.  ;

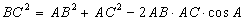2.  ;

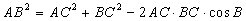3.  .

Доказательство.

Одно из самых красивых и простых доказательств теоремы косинусов является доказательство её в координатной плоскости.

Внесём в координатную плоскость произвольный треугольник ABC так, чтобы точка А совпала с началом координат, а прямая АВ лежала на прямой ОХ. Введём обозначения AB=c,AC=b,CB=a, a угол CAB=α(пока будем считать что α≠90°).
Тогда точка A имеет координаты (0;0), точка B(c;0). Через функцию sin и cos, а также сторону АС=b выведем координаты точки С. С(b×cosα;b×sinα). Координаты точки С остаются неизменными при тупом и остром угле α.
Зная координаты С и B, а также зная, что CB=a, найдя длину отрезка, мы можем составить равенство:



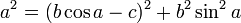
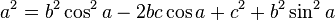
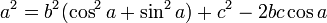
Так как
 (основное тригонометрическое тождество), то

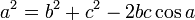
Теорема доказана.
Стоит отметить, что для прямого угла α, теорема также работает cos90°=0 и a²=b²+с² - известная всем теорема Пифагора.

1. Закрепление материала:

Задачи по готовым чертежам. Чертежи проектируются при помощи кодоскопа. При решении задач учащиеся каждый раз проговаривают формулировку теоремы.

Задача 1

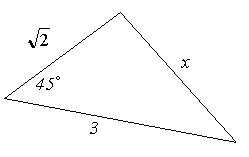
Ответ:  .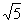

Задача 2

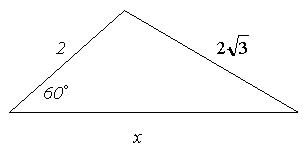
Ответ: 4.

Задача 3

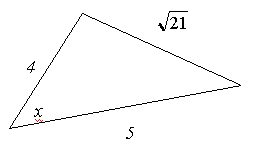
Ответ: 60°.

3.Итог урока

Проводится тест

1. Если квадрат стороны треугольника равен сумме квадратов двух других его сторон, то эта сторона лежит против:

а) тупого угла
б) прямого угл
в) острого угла

1. В  АВС известны длины сторон АВ и ВС. Чтобы найти сторону АС, необходимо знать величину:

а) угла А
б) угла В
в) угла С

1. Треугольник со сторонами 5, 6 и 7 см:

а) остроугольный
б) прямоугольный
в) тупоугольный

1. Если в  АВС   А=48°; 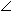  В=72°, то наибольшей стороной треугольника является сторона:

а) АВ
б) АС
в) ВС

1. Если квадрат стороны треугольника больше суммы квадратов двух других его сторон, то эта сторона лежит против:

а) острого угла
б) прямого угла
в) тупого угла

Самопроверка. Ответы:

4.Домашняя  работа: п. 98  №1025(б, в, г).