Условия задач школьного этапа олимпиады по математике в 7 классе

Условия задач школьного этапа олимпиады по математике в 7 классе

Задача № 1:

Квадрат числа состоит из цифр 0, 2, 3, 5. Найти его.(2бал.)

Задача № 2:

В магазин привезли 25 ящиков с яблоками трех сортов,
причем в каждом ящике лежали яблоки какого-то одного сорта.
Можно ли найти 9 ящиков с яблоками одного сорта?(3бал.)

Задача № 3:

Дан угол и точка M внутри него.
Провести прямую через эту точку так, чтобы ее отрезок между сторонами угла делился данной точкой пополам.(4бал.)

Задача № 4:

Автомобиль из A в B ехал со средней скоростью 50 км/ч., а обратно возвращался со скоростью 30 км/ч.
Какова его средняя скорость?(4бал.)

Задача № 5:

Ребятам дали задания перевести скорость черепахи из сантиметров в секунду в метры в минуту. Маша получила ответ 25 м/мин, но при этом считала, что в метре 60 см, а в минуте 100 секунд. Помогите Маше найти правильный ответ.( 6бал.)

Задача № 6:

В некоторый момент времени Аня измерила угол между часовой и минутной стрелками своих часов. Ровно через один час она снова измерила угол между стрелками. Угол оказался таким же. Каким мог быть этот угол?(6бал.)

(Разберите все случаи.)

Решения задач олимпиады

Задача № 1:

3025 = 55².

Задача № 2 :

1) 25:3= 8(ост 1)ящиков каждого, если поровну;

значит если все по 8 и остался ещё 1ящик;

2) 8+1=9ящиков какого-то сорта яблок;

Ответ: да, можно найти 9ящиков одного сорта.

Задача № 3:
Сделать точку M центром параллелограмма.

Пусть А - вершина угла.
1) Продолжим отрезок АМ за точку М на свою длину до точки С. (AM=MC)
2) Через точку C проведем прямые параллельные сторонам угла до их пересечения со сторонами угла в точках B и D. Тогда ABCD - параллелограмм, М - середина диагонали AC, значит М - середина диагонали BD (т.к. диагонали параллелограмма точкой пересечения делятся пополам), что и требовалось

Задача № 4:
Пусть весь путь равен S, тогда время туда s/50, обратно s/30, общее время в пути (туда-обратно) :
s/50 + s/30 = 8s/150
Средняя скорость это отношение всего пути (2s) ко времени (8s/150), получаем:
V = 2s : 8s/150 = 2s * 150 / 8s = 37,5 км/ч

Задача №5

Решение. Черепаха за одну Машину «минуту» преодолевает расстояние в 25 Машиных «метров», то есть за 100 секунд проползает 25 · 60 сантиметров. Тогда скорость черепахи равна (25·60)/100 = 15 см/сек. Значит, за 60 секунд черепаха проползет 15 · 60 сантиметров, то есть (15·60)/100  = 9 метров.

Ответ: 9 м/мин.

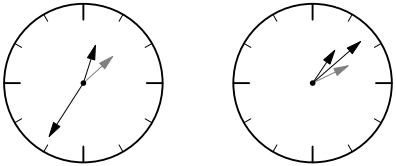
Задача №6

Решение. Через 1 час минутная стрелка остается на своем месте. При этом часовая стрелка повернулась на 30°. Раз угол не изменился, то минутная стрелка делит пополам один из углов между положениями часовой стрелки (либо тот, который 30°, либо дополнительный угол в 330°). Ответ: 15° либо 165°.