Векторы ( геометрия 9 класс)

Муниципальное бюджетное общеобразовательное учреждение

«средняя общеобразовательная школа №4»

Презентации к урокам математики

Заслуженный учитель РФ

Кулиашвили Елена Николаевна

Историческая справка

• Термин вектор (от лат. Vector – “ несущий “) впервые появился в 1845 г. у ирландского математика Уильяма Гамильтона (1805 – 1865) в работах по построению числовых систем.

Что такое вектор ?

Понятие вектора возникает там, где приходится иметь дело с объектами, которые характеризуются величиной и направлением: например, скорость, сила, давление. Такие величины называются векторными величинами или векторами .

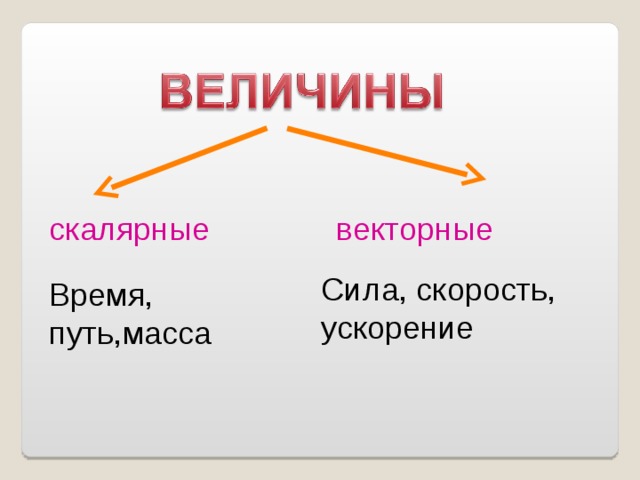
скалярные

векторные

Сила, скорость, ускорение

Время, путь,масса

ВЕКТОР или направленный отрезок – отрезок, у которого указано, какая из его граничных точек считается началом, а какая -- концом

В

А

Конец вектора

Начало вектора

Вектор АВ

• векторы обозначают двумя заглавными латинскими буквами со стрелкой над ними или одной строчной латинской буквой со стрелкой над ней
• любая точка плоскости является нулевым вектором
• длиной или модулем ненулевого вектора АВ называется длина отрезка АВ

Длина вектора

• Расстояние между началом и концом вектора называется длиной или модулем вектора. Длина вектора обозначается |а| или |АВ|.
• Длина нулевого вектора считается равной нулю.

A

B

|AB| = 6 |CD| = 5

|a| = 5 |NN| = 0

(каждая клетка на рисунке имеет сторону, равную единице измерения отрезков)

C

a

D

N

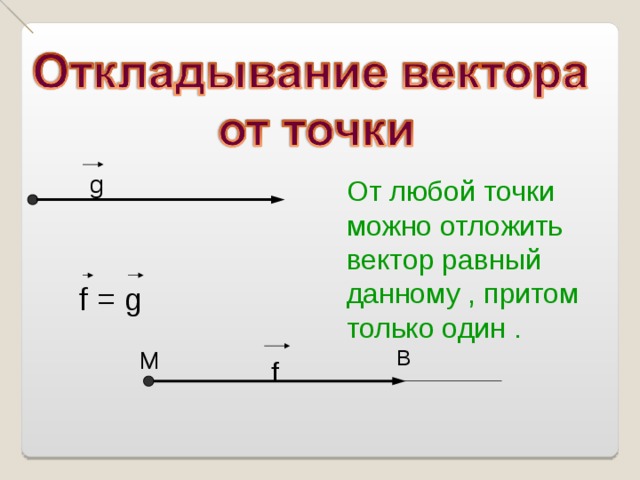
g

От любой точки можно отложить вектор равный данному , притом только один .

f = g

M

B

f

• ненулевые векторы называются коллинеарными , если они лежат либо на одной прямой, либо на параллельных прямых
• коллинеарные векторы могут быть направлены одинаково и называются сонаправленными или противоположно направлены и называются противоположно направленными

Коллинеарные векторы

• Ненулевые векторы называются коллинеарными , если они лежат либо на одной прямой, либо на параллельных прямых.
• Нулевой вектор считается коллинеарным любому вектору.

O

b

CD, KF, O, a, b – коллинеарные

O, a – коллинеарные

O, NP – коллинеарные

NP, m – не коллинеарные

N

D

a

K

P

F

C

m

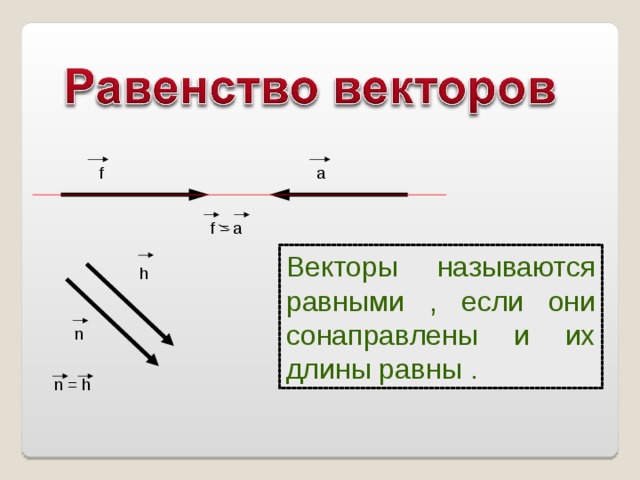
a

f

f = a

Векторы называются равными , если они сонаправлены и их длины равны .

h

n

n = h

Задача

• Какие из векторов, изображенных на рисунке:

• коллинеарны;
• сонаправлены;
• противоположно направлены;
• имеют равные длины?

Отложите эти векторы от одной точки.

d

c

a

b

Задача

• На рисунке изображена равнобедренная трапеция KLMN.

а) Укажите сонаправленные, противоположно направленные, равные вектора.

б) Укажите векторы, длины которых равны. Равны ли при этом сами векторы?

L

M

K

N

Задачи

• Даны вектор BC и точка D(1;-2). Отложите от точки D вектор, равный вектору BC.
• Как должен быть расположен ненулевой вектор a относительно прямой k , чтобы нашлись лежащие на этой прямой векторы, равные a ? Сколько таких векторов найдется? Отметьте на чертеже три из них.
• Векторы AB и DC равны. Докажите, что если точки A, B, C и D не лежат на одной прямой, то четырехугольник ABCD ― параллелограмм.

• На рисунке изображен параллелограмм ABCD.Укажите векторы, длины которых равны. Равны ли при этом сами векторы?

• В ромбе ABCD l AC l = 12см, l BD l = 16см. От вершины A отложен вектор AE, равный вектору BD. Найдите длину вектора EC.

B

C

A

D

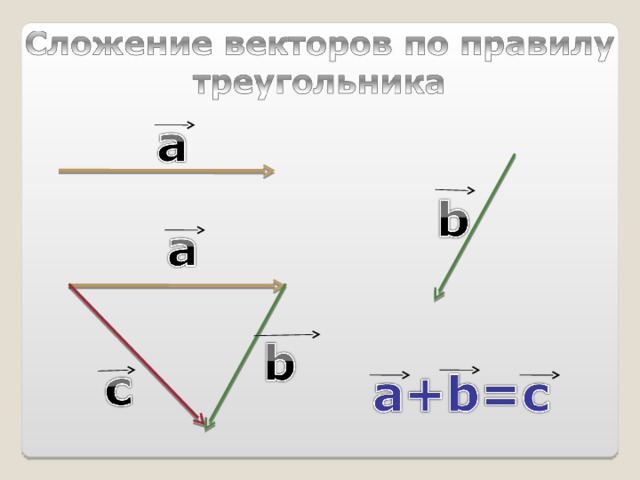
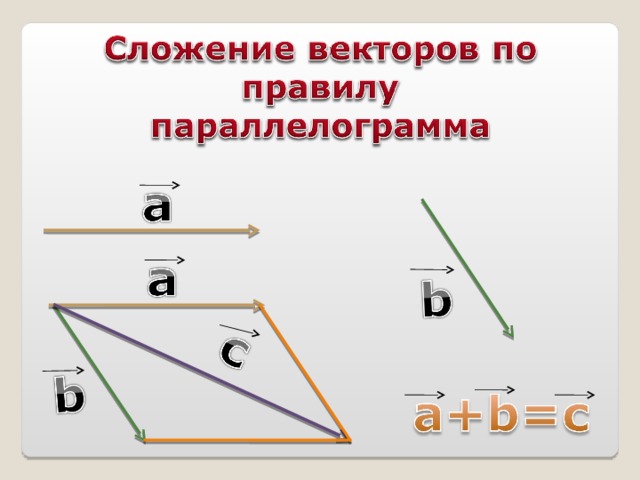
Для любых чисел k , l и любых векторов a , b справедливы равенства :

Для любых чисел k , l и любых векторов a , b справедливы равенства :

• (kl )a = k (la ) ( сочетательный закон )
• (k+l) a = ka + la ( первый распределительный закон )
• K ( a+b ) = ka + kb (второй распределительный закон ) .

• (kl )a = k (la ) ( сочетательный закон )
• (k+l) a = ka + la ( первый распределительный закон )
• K ( a+b ) = ka + kb (второй распределительный закон ) .

а

2а

3а