Векторы. Решение задач

Четырнадцатое октября

Применение векторов к решению задач

Для дальнейшей работы с данной презентацией вам необходимо сохранить её на ваше устройство.

• Сегодня мы рассмотрим примеры решения задач с применением векторов.

АВС D – ромб. Е ВС, ВЕ : ЕС = 3 : 1,

К – середина DC , АВ = , AD = . Выразите через

векторы и векторы:

Задача

a

b

a

b

В

AE

a

AK

E

А

С

Гаврилова Н.Ф. «Поурочные разработки по геометрии: 9 класс». – М.: ВАКО, 2007. – 320 с. – (В помощь школьному учителю)

b

K

D

3

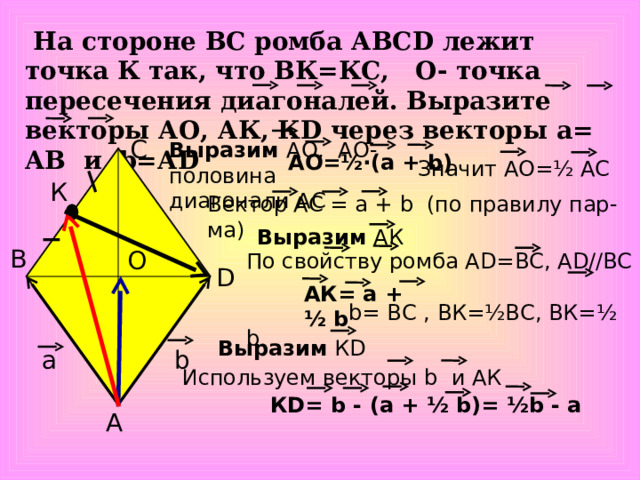
На стороне ВС ромба АВС D лежит точка К так, что ВК=КС, О- точка пересечения диагоналей. Выразите векторы АО, АК, К D через векторы а= АВ и b= А D

С

Выразим АО, АО-половина

диагонали АС

АО=½∙(а + b)

Значит АО=½ АС

К

Вектор АС = а + b (по правилу пар-ма)

Выразим АК

В

О

По свойству ромба А D= ВС, А D// ВС

b= ВС , ВК=½ВС, ВК=½ b

D

АК= а + ½ b

Выразим К D

а

b

Используем векторы b и АК

К D = b - (а + ½ b )= ½ b - a

А

На сторонах С D квадрата АВС D лежит точка Е так, что СЕ=Е D , О-точка пересечения диагоналей. Выразите векторы ВО, ВЕ через векторы а=ВА, b =АС

Дано : ABCD - квадрат. АВ=а, АС= b

Найти : ВО, ВЕ

Решение :

ВА+АО=ВО

АО=½АС

АО=½ b

ВО=а + ½ b

ВЕ=ВС + СЕ,

СЕ=½С D , С D =ВА=а

СЕ=½ a ,

ВС=ВА+АС= а + b

ВЕ= (а + b )+½а

На сторонах С D квадрата АВС D лежит точка P так, что С P = PD , О-точка пересечения диагоналей. Выразите векторы ВО, ВР, РА через векторы а=ВА, b =ВС

Дано : ABCD - квадрат. АВ=а, АС= b

Найти : ВО, ВР, РА

Решение :

ВО=½В D

ВО=½(а + b )

В D =а + b

В D= ВА+ВС

B Р=ВС+ СР

B Р= b +½а

СР=½С D ,

С D =ВА=а,

СР=½С D=½ a

РА=Р D + DA

Р D =½ CD

DA =- b

Р D =½а

D А и ВС –противоположные, DA =- b

РА=½а - b

РА=½а + (- b )

или РА = ВА-ВР

РА = а – ( b +½а)=½а- b

На сторонах ВС и С D параллелограмма АВС D

отмечены точки К и Е так, что ВК=КС, СЕ : Е D =2 : 3 Выразите векторы АК, АЕ, КЕ через векторы х=АВ, у =AD

Дано : ABCD - параллелограмм.

B К=К C, СЕ : Е D= 2 : 3.

Найти : АК, АЕ, КЕ

Решение :

АК=АВ+ВК

ВК=½ВС=½у

АК=х+½у

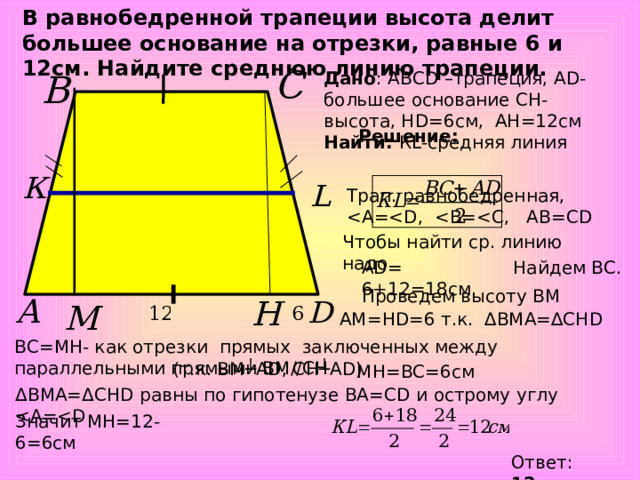
В равнобедренной трапеции высота делит большее основание на отрезки, равные 6 и 12см. Найдите среднюю линию трапеции.

Дано : АВС D –трапеция, А D -большее основание СН-высота, Н D =6см, АН=12см

Найти : К L -средняя линия

Решение :

Трап. равнобедренная,

Чтобы найти ср. линию надо

А D= 6 +12=1 8 c м.

Найдем ВС.

Проведем высоту ВМ

АМ=Н D =6 т.к. ∆ВМА=∆СН D

ВС=МН- как отрезки прямых заключенных между параллельными прямыми ВМ //CH

( т.к. ВМ ┴А D , СН┴А D )

МН=ВС=6см

Δ ВМА= Δ СН D равны по гипотенузе ВА=С D и острому углу

Значит МН=12-6=6см

Ответ : 12см

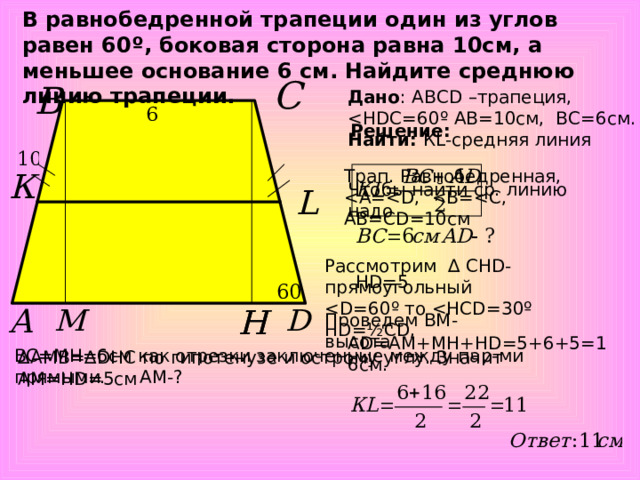
В равнобедренной трапеции один из углов равен 60 º , боковая сторона равна 10см, а меньшее основание 6 см. Найдите среднюю линию трапеции.

Дано : АВС D –трапеция,

Найти : К L -средняя линия

Решение :

Трап. Равнобедренная,

Чтобы найти ср. линию надо

Рассмотрим ∆ СН D- прямоугольный

Н D =5

Проведем ВМ-высота

AD =АМ+МН+Н D =5+6+5=16см.

ВС=МН=6см как отрезки заключенные между пар-ми прямыми. АМ- ?

∆ АМВ=∆ DHC по гипотенузе и острому углу. Значит АМ=Н D =5см

Домашнее задание

№ 1 Выразить векторы ВС, CD, AC, OC, OA через векторы а и b

№ 2 Выразить векторы DP , DM, AC через векторы а и b