Россия, с. Смоленское
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 19.05.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 16.05.2025 08:38
Мерчалова Надежда Ивановна
Преподаватель математики
57 лет
18 353
1 700 
Местоположение
Специализация
Виды симметрий в пространстве.
Категория:
Математика
24.01.2022 17:51
Просмотр содержимого документа
«Виды симметрий в пространстве.»
Виды симметрий в пространстве. Симметрия многогранников.
Движением называется преобразование, при котором сохраняются расстояния между точками.
Под движением пространства понимается отображение пространства на себя, при котором любые две точки A и B переходят (отображаются) в некие точки A1 и B1 так, что |AB| = |A1B1|
При движении в пространстве
- прямые переходят в прямые,
- полупрямые — в полупрямые,
- отрезки — в отрезки,
- сохраняются углы между прямыми.
Виды движения в пространстве
| 1. Центральная симметрия (симметрия относительно точки):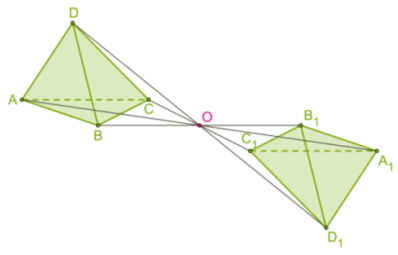
| 2. Осевая симметрия (симметрия относительно прямой):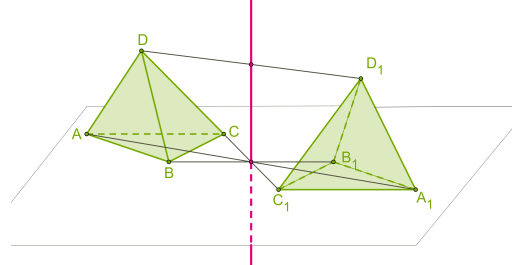
|
| 3. Зеркальная симметрия (симметрия относительно плоскости):
| 4. Параллельный перенос (точки переносятся на данный вектор):
|
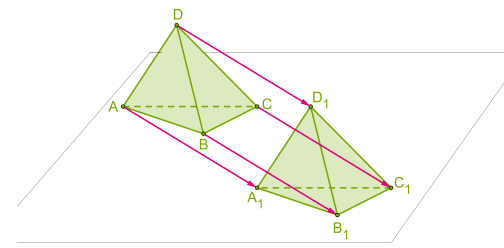
Симметрия – это закономерная повторяемость элементов (или частей) фигуры или какого-либо тела, при которой фигура совмещается сама с собой при некоторых преобразованиях (вращение вокруг оси, отражение в плоскости).
Понятие симметрии включает в себя такие понятия, как: ось симметрии, центр симметрии и плоскость симметрии.
1) Ось симметрии - воображаемая ось, при повороте вокруг которой на некоторый угол, фигура совмещается сама с собой в пространстве
2) Центр симметрии - это точка внутри многогранника, в которой пересекаются и делятся пополам прямые, соединяющие одинаковые элементы многогранника (грани, рёбра, углы)
3) Плоскость симметрии делит многогранник на 2 зеркально равные части
Симметрия в кубе.
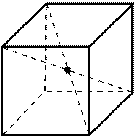
| Центр симметрии (центр куба) - точка пресечения диагоналей куба
|
|
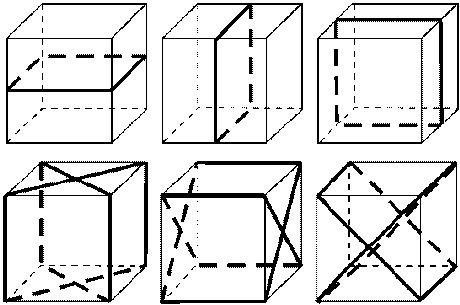
| Плоскости симметрии (9): 3 плоскости симметрии, проходящие через середины параллельных ребер и 6 плоскостей симметрии, проходящие через противолежащие ребра
|
|
| Оси симметрии (13): 3 оси, проходящие через центры противолежащих граней; 4 оси симметрии, проходящие через противолежащие вершины; 6 осей, проходящие через середины противолежащих рёбер |
|
Симметрия в параллелепипеде.
| Центр симметрии - точка пересечения диагоналей прямоугольного параллелепипеда. |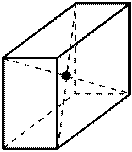
|
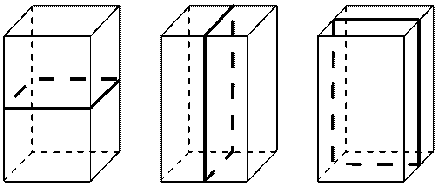
| Плоскость симметрии. 3 плоскости симметрии, проходящие через середины параллельных рёбер.
|
|
| Оси симметрии. 3 оси симметрии, проходящие через точки пересечения диагоналей противолежащих граней
|
|
Симметрия в призме.
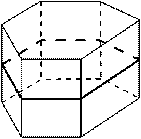
| Симметрия прямой призмы Одна плоскость симметрии, проходящая через середины боковых рёбер
|
|
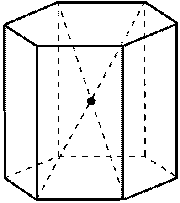
| Симметрия правильной призмы Центр симметрии При чётном числе сторон основания центр симметрии - это точка пересечения диагоналей правильной призмы
|
|
| Плоскости симметрии: плоскость, проходящая через середины боковых рёбер; при чётном числе сторон основания - плоскости, проходящие через противолежащие рёбра |
|
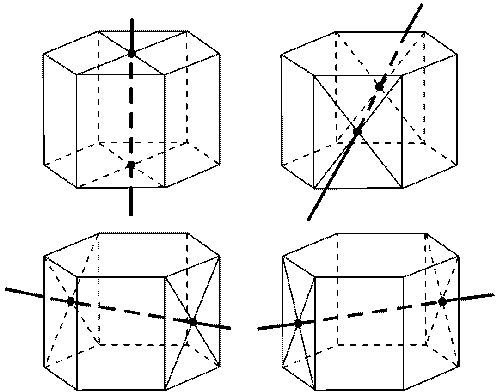
| Ось симметрии: при чётном числе сторон основания - ось симметрии проходит через центры оснований; оси симметрии, проходящие через точки пресечения диагоналей противолежащих боковых граней
|
|
Симметрия в пирамиде.
| Плоскости симметрии: при четном числе сторон основания — плоскости, проходящие через противолежащие боковые ребра и плоскости, проходящие через медианы, проведенные к основанию противолежащих боковых граней |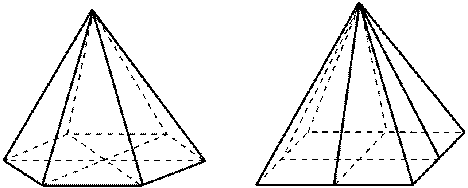
|
| Ось симметрии: при четном числе сторон основания — ось симметрии проходит через вершину правильной пирамиды и центр основания |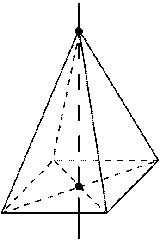
|
Выполнить тест по теме
«Виды симметрий в пространстве. Симметрия многогранников»
-
Сколько центров симметрии имеет параллелепипед?
-
Сколько осей симметрии имеет правильный треугольник?
-
Сколько плоскостей симметрии имеет правильная четырехугольная пирамида?
-
Какие из следующих печатных букв имеют ось симметрии?
а) И
б) В
в) Ж
г) Р
-
Какие из следующих печатных букв имеют центр симметрии?
а) Р
б) О
в) Ж
г) Д
-
Дан куб ABCDA1B1C1D1. О - точка пересечения его диагоналей. Какая точка симметрична вершине С1 относительно точки О?
-
Дан куб ABCDA1B1C1D1. О - точка пересечения его диагоналей. Какой отрезок симметричен ребру С1B1 относительно точки О?
а) BC
б) AD
в) A1D1
г) AB
-
Дан куб ABCDA1B1C1D1. О - точка пересечения его диагоналей. Какой отрезок симметричен ребру С1C относительно плоскости BB1D1?
а) AC
б) A1C1
в) A1A
г) BB1
-
Фигура обладает зеркальной симметрией, если она имеет ...
а) центр симметрии
б) ось симметрии
в) середину
г) плоскость симметрии
-
Плоскость имеет ...
а) центр симметрии
б) плоскость симметрии
в) середину
г) ось симметрии
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
