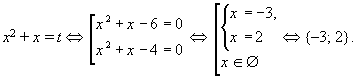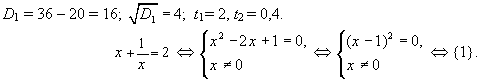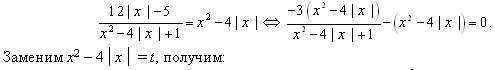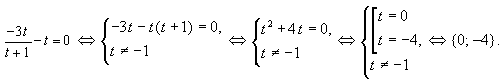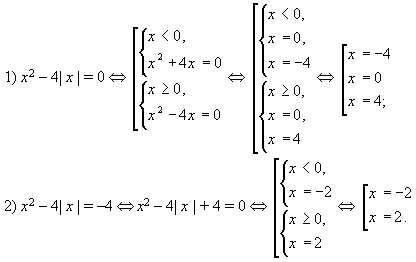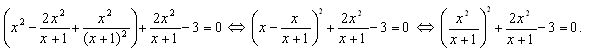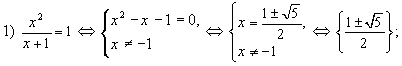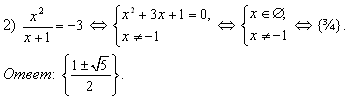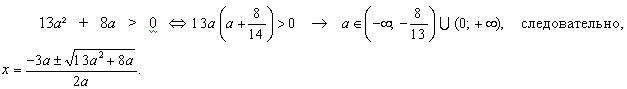Проектная работа по теме:
Виды уравнений и способы их решения
ВЫПОЛНИЛА:
Шериев Алим,
обучающийся 9В класса
РУКОВОДИТЕЛЬ:
Танашева З.Х.,
учитель математики
2023-2024
Оглавление
Введение……………………………………………………….…………….....стр. 3
РАЗДЕЛ I. Теоретическая часть
Сведения из истории уравнений…………………….………………....стр. 4
Основные понятия и свойства уравнений……………………………..стр. 6
Классификация уравнений..……………………………………..…….стр. 7
Стандартные методы решения уравнений.….………….………….....стр. 8
Нестандартные методы решения уравнений………………………...стр. 14
РАЗДЕЛ II. Практическая часть
2.1. Решение уравнений из второй части ОГЭ……………………………..стр. 19
2.2. Решение уравнений нестандартными способами………………….….стр. 22
Заключение…………………………………………………………….……..стр. 24
Список используемой литературы……………..………………………..….стр. 25
Приложение 1. Дидактический материал по решению уравнений
второй части ОГЭ…………………………………………………….….….стр. 26
Приложение 2. Дидактический материал по решению уравнений
более высокого уровня………………..…………………………………….стр. 27
Введение
Мне приходится делить своё время между
политикой и уравнением. Однако уравнение,
по-моему, гораздо важнее, потому что политика
существует только для данного момента,
а уравнение будет существовать вечно.
Альберт Эйнштейн
Практически всё, что окружает современного человека - это все так или иначе связано с математикой. А последние достижения в физике, технике и информационных технологиях не оставляют никакого сомнения, что и в будущем положение вещей останется прежним. Поэтому решение многих практических задач сводится к решению различных видов уравнений, которые достаточно часто сводятся к уравнениям второй степени (квадратным).
Теория уравнений в школьном курсе алгебры занимает ведущее место. На их изучение отводится времени больше, чем на любую другую тему школьного курса математики. Это связано с тем, что большинство жизненных задач сводится к решению различных видов уравнений.
Актуальность этой темы заключается в том, что на уроках алгебры, геометрии, физики, химии, биологии мы очень часто встречаемся с решением уравнений. Многие обучающиеся, сдающие ОГЭ по математике, мечтают набрать высший балл. Для этого надо уметь решать уравнения, так как умение решать уравнения встречается в нескольких заданиях в КИМ ОГЭ. Поэтому каждому выпускнику важно научиться решать уравнения, выбирая и применяя рациональный способ решения.
Для себя я определил проблемный вопрос: «Какие способы решения уравнений надо знать для успешного выполнения КИМ ОГЭ и для решения жизненных задач?» Поэтому я выбрал тему исследования, связанную с уравнениями, в ходе работы она получила название «Виды уравнений и способы их решения».
Цель работы: изучить виды уравнений и различные способы их решения, научиться применять их при решении и выбирать наиболее рациональный способ решения.
Исходя из данной цели, мною были поставлены следующие задачи:
- изучить историю развития уравнений;
- представить классификацию уравнений;
- рассмотреть стандартные и нестандартные методы решения уравнений;
- анализ КИМ ОГЭ;
- научиться решать уравнения различными способами;
- разработать дидактический материал и провести его апробацию на математическом кружке в 8 классе;
- разработать памятку по способам решения уравнений для одноклассников.
Объект исследования: уравнения.
Предмет исследования: способы решения уравнений.
Вид проекта: информационно-исследовательский.
Ход работы над проектом:
1. Изучение литературы по истории вопроса
2. Обобщение накопленных знаний об уравнениях и способах их решения из школьной программы
3. Изучение дополнительной литературы и других источников информации
4. Систематизация приемов решения уравнений
5. Разработка дидактического материала и памятки для одноклассников
6. Проведение занятия с обучающимися 8 класса
7. Защита проекта
РАЗДЕЛ I. Теоретическая часть
Сведения из истории уравнений
История изучения уравнений насчитывает много веков. Ещё за 3–4 тысячи лет до н.э. египтяне и вавилоняне, пользуясь таблицами и готовыми выработанными рецептами, умели решать некоторые уравнения. Разумеется, приёмы решения у них были вовсе не такими, как теперь. Греки, унаследовавшие математические знания египтян и вавилонян пошли дальше.
Наибольших успехов в решении уравнений добился выдающийся древнегреческий учёный. Диофант (III век), которого по праву называют «отцом алгебры».

Диофант умел решать очень сложные уравнения, примеряя для неизвестных буквенные обозначения, ввёл специальный символ для вычитания, использовал сокращения слов.
О нём потом писали:
Посредством уравнений, теорем
Он уйму всяких разрешил проблем:
И засуху предсказывал, и ливни –
Поистине его познанья дивны.
Стройное учение об уравнениях разработал среднеазиатский учёный Мухаммед аль-Хорезми (IX в.). Он написал книгу «Китабаль – Джебр Валь-Мукабала», что означает «Книга о восстановлении и противопостановлении». Это был первый в мире учебник алгебры. С этого времени алгебра становится самостоятельной наукой. Само слово «алгебра» произошло от слова «аль-фкебр» – восполнение: так аль-Хорезми называл перенос отрицательных слагаемых из одной части уравнения в другую с переменой знака.
В дальнейшем проблема решений уравнений занимала умы всех математиков.
Самыми известными математиками, внесшими вклад в развитие теории уравнений, были:
Архимед (около 287–212 до н. э. ) - древнегреческий ученый, математик и механик. При исследовании одной задачи, сводящейся к кубическому уравнению, Архимед выяснил роль характеристики, которая позже получила название дискриминанта.
Франсуа Виет жил в XVI в. Он внес большой вклад в изучение различных проблем математики. В частности, он ввел буквенные обозначения коэффициентов уравнения и установил связь между корнями квадратного уравнения.
Леонард Эйлер (1707 – 1783) - математик, механик, физик и астроном. Автор св. 800 работ по математическаму анализу, дифференциальных уравнений, геометрии, теории чисел, приближённым вычислениям, небесной механике, математике, оптике, баллистике, кораблестроению, теории музыки, и т. д. Оказал значительное влияниена развитие науки. Вывел формулы (Формулы Эйлера), выражающие тригонометрические функции переменного х через показательную функцию.
Лагранж Жозеф Луи (1736 — 1813 гг. ), французский математик и механик. Ему принадлежат выдающиеся исследования, среди них исследования по алгебре (симметрической функции корней уравнения, по дифференциальным уравнениям (теория особых решений, метод вариации постоянных).
Ж. Лагранж и А. Вандермонд - французские математики. В 1771 г. впервые применили способ решения систем уравнений (способ подстановки).
Гаусс Карл Фридрих (1777 —1855 гг. ) - немецкий математик. Написал книгу, в которой излагается теория уравнений деления круга (т. е. уравнений xn — 1 = 0), которая во многом была прообразом Галуа теории. Помимо общих методов решения этих уравнений, установил связь между ними и построением правильных многоугольников. Он, впервые после древнегреческих учёных, сделал значительный шаг вперёд в этом вопросе, а именно: нашёл все те значения n, для которых правильный n-угольник можно построить циркулем и линейкой. Изучал способ сложения. Сделал вывод, что системы уравнений можно между собой складывать, делить, и умножать.
О. И. Сомов – обогатил разные части математики важными и многочисленными трудами, среди них теория определённых алгебраических уравнений высших степеней.
Галуа Эварист (1811—1832 гг. ), - французский математик. Основной его заслугой является формулировка комплекса идей, к которым он пришёл в связи с продолжением исследований о разрешимости алгебраических уравнений, начатых Ж. Лагранжем, Н. Абелем и др. , создал теорию алгебраических уравнений высших степеней с одним неизвестным.
А. В. Погорелов (1919 – 1981 гг. ) - В его творчестве связаны геометрические методы с аналитическими методами теории дифференциальных уравнений с частными производными. Его труды оказали существенное влияние также на теорию нелинейных дифференциальных уравнений.
П. Руффини - итальянский математик. Посвятил ряд работ, доказательству неразрешимости уравнения 5-й степени, систематически использует замкнутость множества подстановок.
Не смотря на то, что ученые давно изучают уравнения, науке не известно, как и когда у людей возникла необходимость использовать уравнения. Известно только, что задачи, приводящие к решению простейших уравнений, люди решали с того времени, как стали людьми. Еще 3 - 4 тысячи лет до н. э. египтяне и вавилоняне умели решать уравнения. Правило решения этих уравнений, совпадает с современным, но неизвестно, как они до этого дошли.
В Древнем Египте и Вавилоне использовался метод ложного положения. Уравнение первой степени с одним неизвестным можно привести всегда к виду ах + Ь = с, в котором а, Ь, с целые числа. По правилам арифметических действий ах = с - b, если Ь с, то с b число отрицательное. Отрицательные числа были египтянам и многим другим более поздним народам неизвестны (равноправно с положительными числами их стали употреблять в математике только в семнадцатом веке). Для решения задач, которые мы теперь решаем уравнениями первой степени, был изобретен метод ложного положения. В папирусе Ахмеса 15 задач решается этим методом. Египтяне имели особый знак для обозначения неизвестного числа, который до недавнего прошлого читали «хау» и переводили словом «куча» («куча» или «неизвестное количество» единиц). Теперь читают немного менее неточно: «ага». Способ решения, примененный Ахмесом, называется методом одного ложного положения. При помощи этого метода решаются уравнения вида ах = b. Этот способ заключается в том, что каждую часть уравнения делят на а. Его применяли как египтяне, так и вавилоняне. У разных народов применялся метод двух ложных положений. Арабами этот метод был механизирован и получен ту форму, в которой он перешел в учебники европейских народов, в том числе в «Арифметику» Магницкого. Магницкий называет способ решения «фальшивым правилом» и пишет в части своей книги, излагающей этот метод: «Зело бо хитра есть сия часть, Яко можеши ею все класть. Не токмо что есть во гражданстве, Но и высших наук в пространстве, Яже числятся в сфере неба, Якоже мудрым есть потреба.»
Содержание стихов Магницкого можно вкратце передать так: эта часть арифметики весьма хитрая. При помощи ее можно вычислить не только то, что понадобится в житейской практике, но она решает и вопросы «высшие», которые встают перед «мудрыми». Магницкий пользуется «фальшивым правилом» в форме, какую ему придали арабы, называя его «арифметикой двух ошибок» или «методой весов».
Основные понятия и свойства уравнений
В алгебре рассматриваются два вида равенств – тождества и уравнения. Остановимся на основных понятиях.
Тождество - это равенство, которое выполняется при всех (допустимых) значениях входящих в него букв. Для записи тождества наряду со знаком = (равно) также используется знак = (равносильности).
Уравнение - это равенство, которое выполняется лишь при некоторых значениях входящих в него букв. Буквы, входящие в уравнение, по условию задачи могут быть неравноправны: одни могут принимать все свои допустимые значения (их называют параметрами или коэффициентами уравнения и обычно обозначают первыми буквами латинского алфавита: a, b, c...); другие, значения которых требуется отыскать, называют неизвестными (их обычно обозначают последними буквами латинского алфавита: х, у). В общем виде уравнение может быть записано так: F (х1, х2, …) = 0. В зависимости от числа неизвестных уравнение называют уравнением с одним, двумя и т. д. неизвестными.
Значение неизвестных, обращающие уравнение в тождество (верное равенство), называют решениями уравнения.
Решить уравнение – это значит найти множество его решений или доказать, что решений нет. В зависимости от вида уравнения множество решений уравнения может быть бесконечным, конечным и пустым.
Если все решения одного уравнения являются решениями другого уравнения, то такие уравнения называют эквивалентными.
Если все корни одного уравнения являются корнями второго уравнения, то второе уравнение называется следствием первого уравнения.
Значения неизвестного х, обращающие алгебраическое уравнение в тождество, называются корнями (решениями) алгебраического уравнения. Про корни говорят, что они удовлетворяют данному уравнению.
С алгебраическими выражениями, входящими в уравнения, можно выполнять операции, которые не меняют его корней, в частности:
к обеим частям уравнения прибавить любую функцию, которая определена при всех значениях из ОДЗ. Следствие. Члены уравнения можно переносить из одной части уравнения в другую;
обе части уравнения умножить на любую функцию, определенную и отличную от нуля при всех допустимых значениях неизвестного. Также можно делить и умножать на число, отличное от нуля;
в обеих частях уравнения стоят функции, принимающие только неотрицательные значения, то при возведении в одну и ту же четную степень получаем уравнение, равносильное данному. Появлению “посторонних корней” приводят преобразования:
а) приведение подобных членов – происходит расширение ОДЗ;
б) сокращение дроби на выражение, содержащие неизвестное (тоже происходит расширение ОДЗ);
в) умножение на выражение, содержащее неизвестное;
г) освобождение дроби от знаменателя, содержащего неизвестное. Необходимо обязательно делать проверку или лучше перейти к смешанной системе.
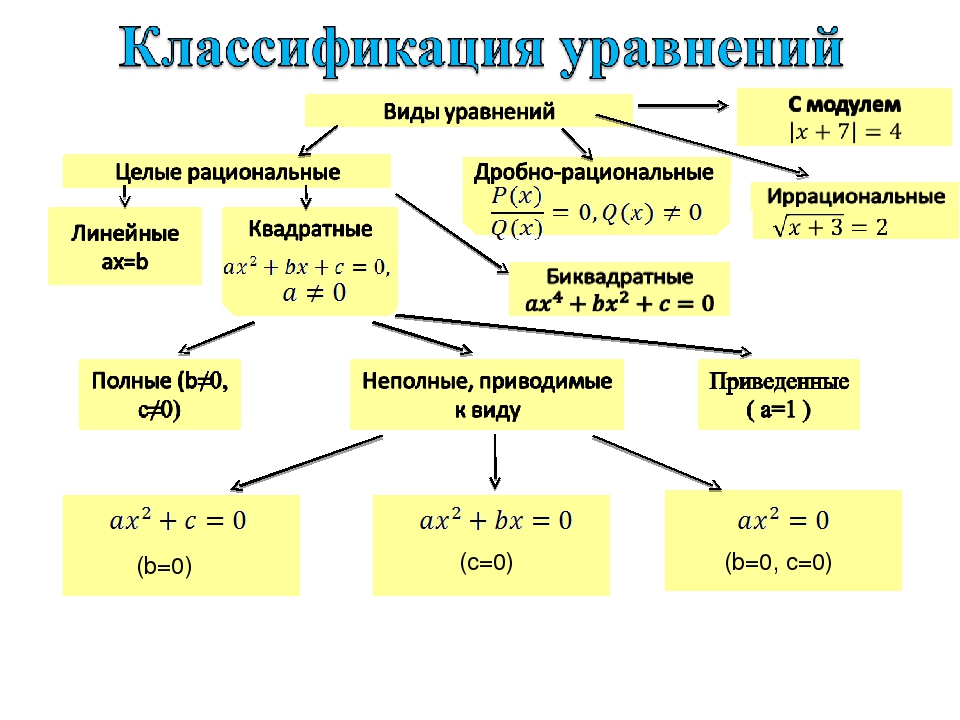
Классификация уравнений
Уравнения подразделяются на две большие группы: алгебраические и трансцендентные. Алгебраическим называется такое уравнение, в котором для нахождения корня уравнения используются только алгебраические действия, а именно четыре арифметических – сложение, вычитание, умножение и деление, а также возведение в степень и извлечение натурального корня. Трансцендентным называется уравнение, в котором для нахождения корня используются не алгебраические функции: например, тригонометрические, логарифмические и иные.
В курсе математики основной школы рассматриваются только алгебраические уравнения. Группу алгебраических уравнений можно условно разделить на такие виды уравнений как:
целые — с обеими частями, состоящими из целых алгебраических выражений по отношению к неизвестным;
дробные — содержащие целые алгебраические выражения в числителе и знаменателе;
иррациональные — алгебраические выражения здесь находятся под знаком корня;
с модулем - алгебраические выражения здесь находятся под знаком модуля.
Дробные, иррациональные и с модулем уравнения можно свести к решению целых уравнений.
Существует также и ещё одна классификация, которая основывается на степени, которая имеется в левой части многочлена. Исходя из этого, различают линейные, квадратные и кубические уравнения. Линейные уравнения также могут называться уравнениями первой степени, квадратные - второй, а кубические, соответственно, третьей.
Стандартные методы решения уравнений
Общие методы решения уравнений можно выделить следующие: по формулам, разложение на множители (вынесение общего множителя за скобки, способ группировки, с помощью формул сокращенного умножения), замена переменной, использование ограниченности и монотонности функций, графически.
Линейные уравнения – это уравнения вида: ах + b = 0, где a и b – некоторые постоянные.
- Если а не равно нулю, то уравнение имеет один единственный корень: х = - b : а ( ах + b; ах = - b; х = - b : а. ).
Например: решить линейное уравнение: 4х + 12 = 0.
Решение: Т. к а = 4, а b = 12, то х = - 12 : 4; х = - 3.
Проверка: 4 ( - 3) + 12 = 0; 0 = 0.
Т. к. 0 = 0, то -3 является корнем исходного уравнения.
Ответ: х = -3
- Если а равно нулю, и b равно нулю, то корнем уравнения ах + b = 0 является любое число.
Например: 0х + 0 = 0;
0 = 0. Т. к 0 равно 0, то корнем уравнения 0х + 0 = 0 является любое число.
- Если а равно нулю, а b не равно нулю, то уравнение ах + b = 0 не имеет корней.
Например:0х – 6 = 0;
0 = 6. Т. к 0 не равно 6, то 0х – 6 = 0 не имеет корней.
Квадратным уравнением (или уравнением второй степени) называется уравнение вида ax²+bx+c=0 , где x – переменная, a, b и c – некоторые числа,
причем a≠0.
- Решение квадратных уравнений по формулам:
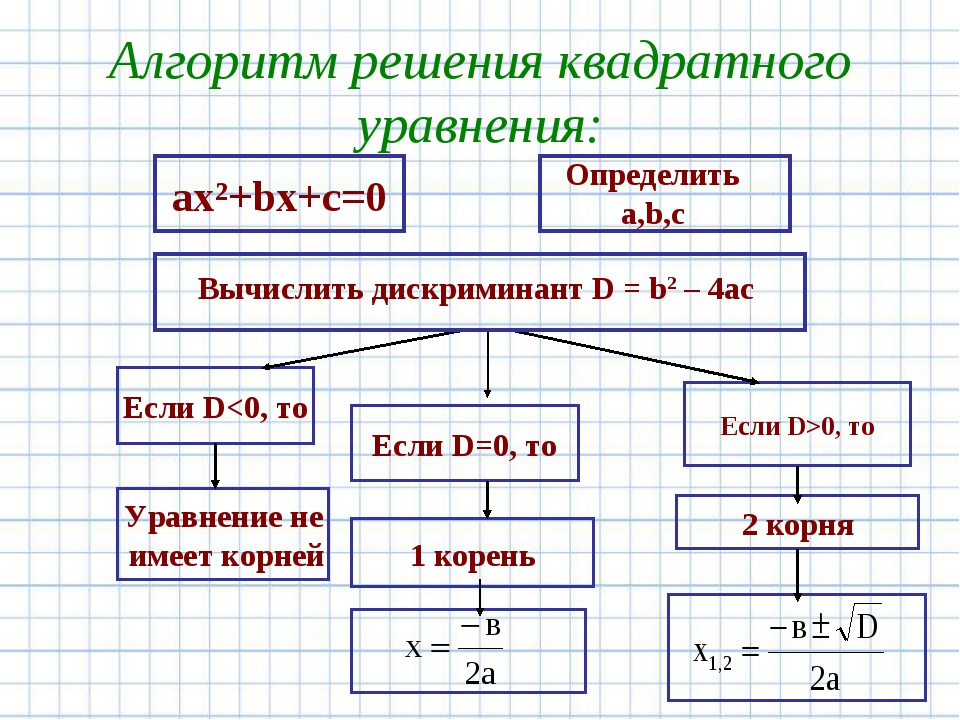
Например: 4х2 - 16х + 15 = 0.
Решение: а = 4, b = - 16, с = 15, D = b2 - 4ac = (-16)2 - 4·4·15= 16, D 0, уравнение имеет два различных корня;
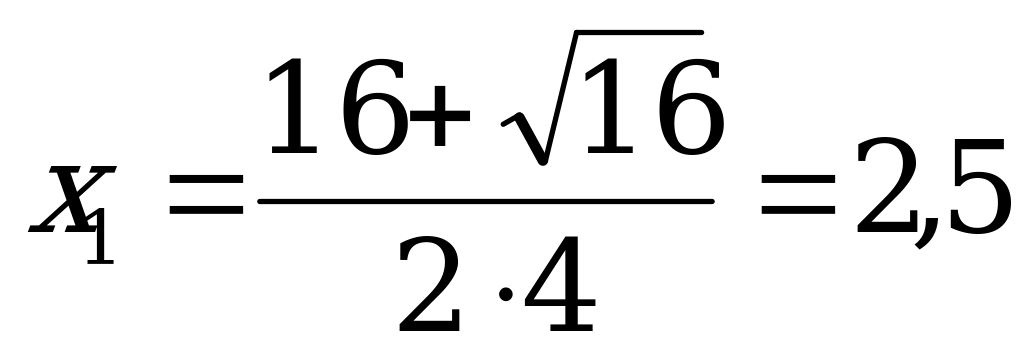 ;
; 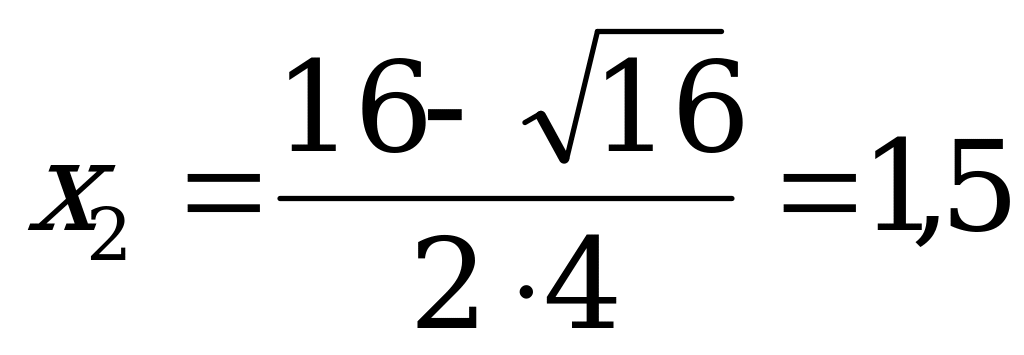
Ответ:1,5; 2,5.
- Решение квадратных уравнений со вторым четным коэффициентом по формулам:

- Решение квадратных уравнений по теореме Виета:
Приведенным квадратным уравнением называется уравнение вида 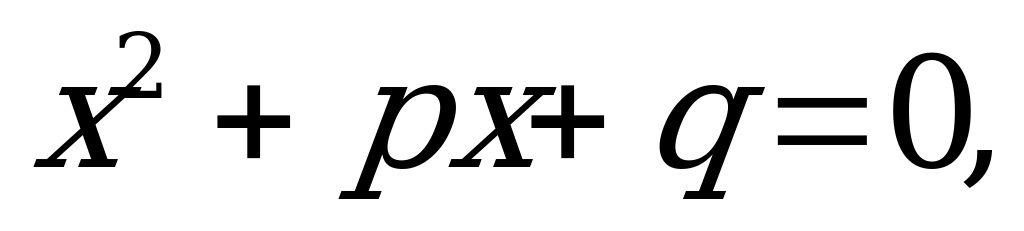 где старший коэффициент равен единице. Корни приведенного квадратного уравнения можно найти по следующей формуле:
где старший коэффициент равен единице. Корни приведенного квадратного уравнения можно найти по следующей формуле: 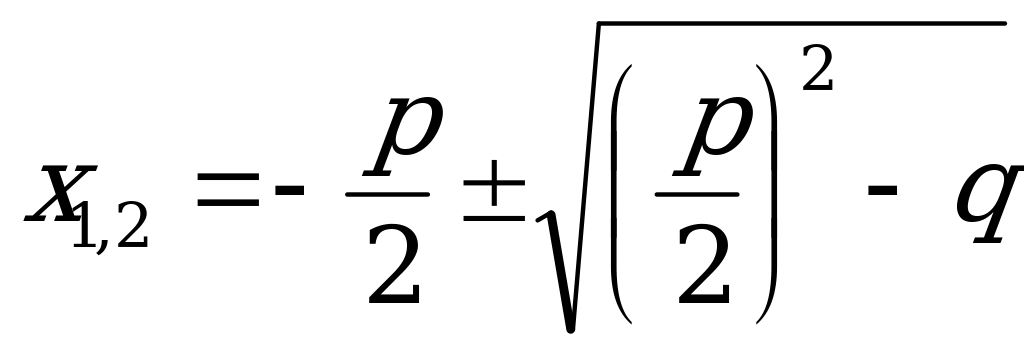 .
.
Запомнить эту формулу можно заучив следующий стишок.
P со знаком взяв обратным
На 2 мы его разделим,
И от корня аккуратно знаком  отделим,
отделим,
А под корнем очень кстати
Половина 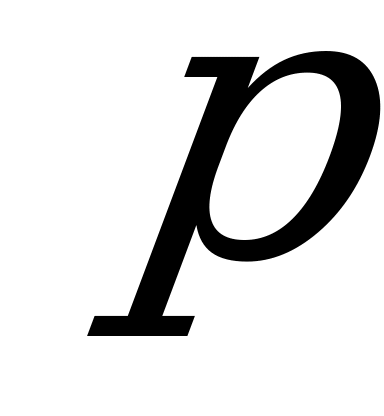 в квадрате,
в квадрате,
Минус 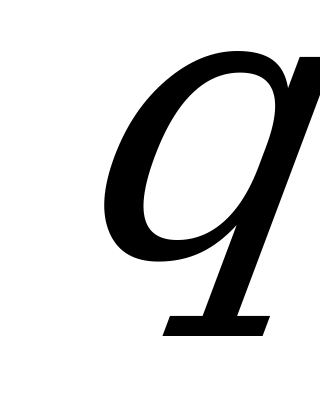 и вот решение небольшого уравнения.
и вот решение небольшого уравнения.
Чтобы квадратное уравнение 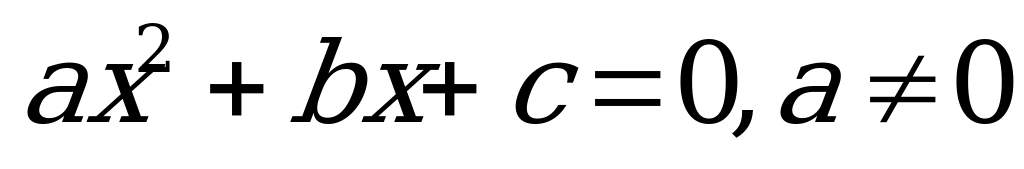 привести к приведенному виду, нужно все его члены разделить на a,
привести к приведенному виду, нужно все его члены разделить на a,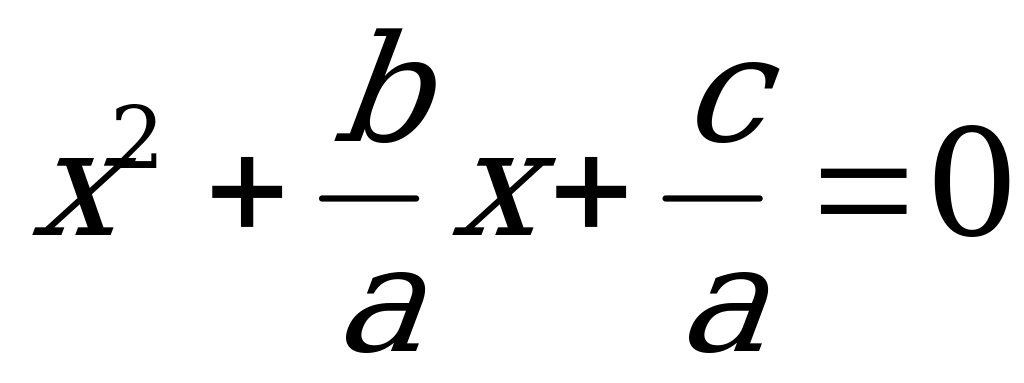 тогда
тогда
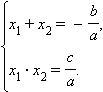
Если обозначить 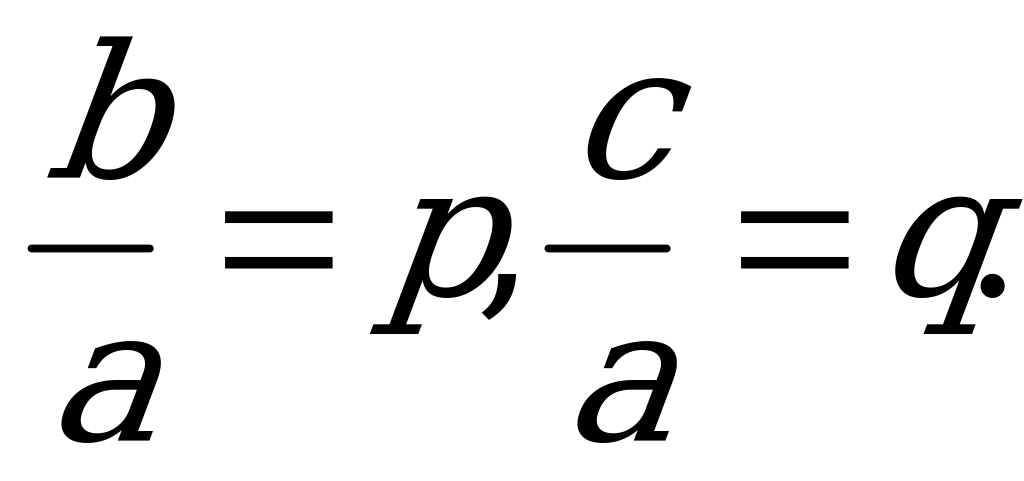 , то мы получим уравнение вида
, то мы получим уравнение вида 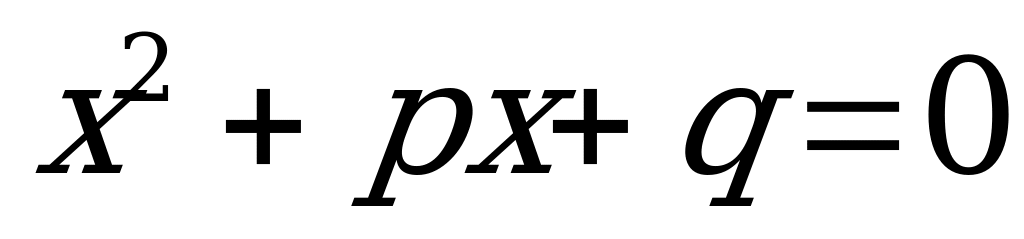 . Таким образом: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену. По коэффициентам p и q можно предсказать знаки корней.
. Таким образом: сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену. По коэффициентам p и q можно предсказать знаки корней.
а) Если сводный член q приведенного уравнения положителен (q 0), то уравнение имеет два одинаковых по знаку корня и это зависит от второго коэффициента:
- если р
- если р 0, то оба корня отрицательные.
б) Если свободный член q приведенного уравнения отрицателен (q 0 .
Например: Решим уравнение 4х2 - 16х + 15 = 0.
Решение. Перейдем к приведенному квадратному уравнению: х2 – 4х + 3,75 = 0, q=3,75 0 ,имеет два одинаковых по знаку корня
p=-41 + х2 = 4, х1 · х2 = 3,75; то х1= 1,5, х2= 2,5
Ответ:1,5; 2,5.
По праву достойна в стихах быть воспета
О свойствах корней теорема Виета.
Что лучше, скажи, постоянства такого:
Умножишь ты корни — и дробь уж готова:
В числителе с, в знаменателе а,
А сумма корней тоже дроби равна.
Хоть с минусом дробь эта, что за беда —
В числителе b, в знаменателе а.
- Решение квадратных уравнений с помощью свойств коэффициентов:
Пусть дано квадратное уравнение ах2+ bх + с = 0, где а ≠ 0.
Если а+ b + с = 0 (т.е. сумма коэффициентов равна нулю), то х1= 1, х2 = с/а.
Если a – b + c=0, то х1 =-1, х2 = -с/а
Например: х2 - 16х + 15 = 0.
Решение: а+ b+ с = 0 1 + (-16) + 15 = 0, то х1= 1, х2 = 15.
Например: 2х2+ 3х +1= 0. Так как 2 - 3+1=0, значит х1 = -1, х2 =-с/а= -1/2
- Решение неполных квадратных уравнений:

Например: а) -3x²+15=0 -3x²=-15 x²=5 x₁=√5 x2=-√5
б) 4x²+9x=0 x(4x+9)=0 x=0 или 4x+9=0
4x=-9
x= -2¼
в) 4x²+3=0 4x²=-3 x²=-¾ - нет корней, а значит и 4x²+3=0 –не имеет корней.
Биквадратное уравнение

Дробно-рациональные уравнения. Пусть f(x) и g(x) – некоторые функции, зависящие от переменной x. Дробно- рациональное уравнение – это уравнение вида f(x)/g(x)=0. Для того, чтобы решить дробно рациональное уравнение, надо вспомнить, что такое ОДЗ и когда оно возникает. ОДЗ – область допустимых значений переменной. В выражении вида f(x)/g(x)=0 ОДЗ: g(x)≠0 (знаменатель дроби не может быть равен нулю).

Например: 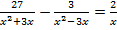
ОДЗ:
То есть 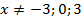 .
.
Перенесем все слагаемые в одну часть уравнения.
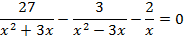
Для того чтобы вычесть дроби, приведем их к общему знаменателю.
Разложим каждый знаменатель на множители:
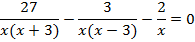
Общий знаменатель – 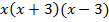 . Домножим первую дробь на
. Домножим первую дробь на 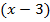 , вторую – на
, вторую – на 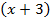 , третью – на
, третью – на 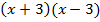
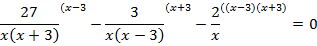
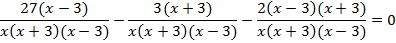
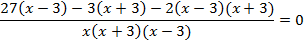
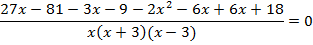
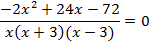
Приравниваем числитель дроби к 0.
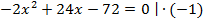
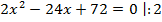
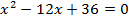
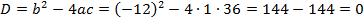

В ОДЗ входят любые значения переменной, кроме 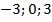 . Значит, число 6 является корнем исходного уравнения.
. Значит, число 6 является корнем исходного уравнения.
Иррациональными уравнениями называются уравнения, в которых переменная содержится под знаком корня. Чтобы решить иррациональное уравнение, надо просто возвести в нужную степень обе части уравнения, а потом решать его как простое рациональное уравнение. Но не забывать про ОДЗ, подкоренное выражение обязано быть неотрицательным.
Например: 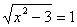
Возведем обе части уравнения в квадрат.
x2 - 3 = 1;
x2 = 4;
Полученное неполное квадратное уравнение имеет два корня -2 и 2.
Произведем проверку полученных корней, для этого произведем подстановку значений переменной x в исходное уравнение.
Проверка.
При x1 = -2 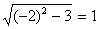 - верно:
- верно:
При x2 = 2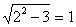 - верно.
- верно.
Отсюда следует, что исходное иррациональное уравнение имеет два корня -2 и 2.
Уравнение с модулем называются уравнения, в которых переменная содержится под знаком модуля. 
Простейшее уравнение с модулем │f(x)│= a равносильно совокупности
f(x)= a или f(x) = -a, если а больше 0 , если же а меньше 0, то уравнение решений не имеет.
Для решения уравнений с модулем чаще всего используют такие методы:
раскрытие модуля по определению;
возведение обеих частей уравнения в квадрат;
метод интервалов.
Например:

Нестандартные методы решения уравнений
1) Метод подбора. Это самый простейший способ. Он заключается в том, что подбирают все допустимые значения неизвестного путём перечисления.
Например:
Решить уравнение.
2х + 2 = 6.
Решение.
Пусть х = 1. Тогда
2 · 1 + 2 = 6;
4 = 6. Т. к 4 не равно 6, то наше предположение, что х = 1 было неверным.
Пусть х = 2.
2 · 2 + 2 = 6;
6 = 6. Т. к 6 равно 6, то наше предположение, что х = 2 было верным.
Ответ: х = 2.
2) Графический способ.
Он заключается в том, что строится график функций данного уравнения. Т. к в линейном уравнение у = 0, то график будет параллелен оси ординат. Точка пересечения графика с осью абсцисс будет решением данного уравнения.
Например:
Решить уравнение.
2х + 3 = 7.
Решение.
Пусть у = 7. Тогда у = 2х + 3.
Построим график функций обоих уравнений
3) Разложение левой части уравнения на множители
Решим уравнение 4х2 - 16х + 15 = 0.
Решение. Разложим левую часть на множители:
4х2 - 16х + 15 = х2 - 10х - 6х +15 = 2х(2х -5) - 3(2х - 5) = (2х - 5)(2х -3).
Следовательно, уравнение можно переписать так:
(2х - 5)(2х - 3) = 0
Произведение множителей равно нулю, если, по крайней мере, один из его множителей равен нулю. 2х - 5= 0 или 2х -3=0
х=2,5 х=1,5
Ответ: 1,5; 2,5.
4) Метод выделения полного квадрата
Решим уравнение 4х2 - 16х + 15 = 0.
Решение. Разделим обе части на 2: х2 - 4х + 3,75 = 0.
Выделим в левой части полный квадрат:
х2- 4х + 3,75 = х2 -2·2 х + 22 - 22 +3,75 = (х -2)2-0,25
тогда, данное уравнение можно записать так:
(х -2)2 -0,25 = 0, (х - 2)2 = 0,25, х - 2= 0,5 или х - 2= - 0,5
х = 2,5 х = 1,5
Ответ:1,5; 2,5.
5) Решение уравнений способом «переброски»
Рассмотрим квадратное уравнение ах2 + bх + с = 0,где а ≠ 0.
Умножая обе его части на а, получаем уравнение а2х2 + аbх +ас = 0.
Пусть ах = у, откуда х = у/а; тогда у2 + by + ас= 0.
Его корни у1и у2 найдем с помощью теоремы Виета и окончательно:
�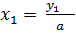 � и �
� и � �.
�.
При этом способе коэффициента умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
Решим уравнение 4х2 - 16х + 15 = 0.
Решение. «Перебросим» коэффициент 4 к свободному члену, в результате получим уравнение у2 – 16у + 60 = 0.
Согласно теореме Виета: у1=6, х1 = 6/4, x1 = 1,5
у2 =10; x2 = 10/4; x2 = 2,5.
Ответ:1,5; 2,5.
6) Графическое решение квадратного уравнения
Квадратное уравнение можно решать и графическим способом. Используя знания о квадратичной и линейной функциях и их графиках, можно решить квадратное уравнение так называемым функционально-графическим методом. Причем некоторые квадратные уравнения можно решить различными способами. Решим графически уравнение ах2+ bх + с = 0. Оно равносильно уравнению ах2 = - (bх + с). Постоим графики функций y = ах2и y = - bх - с в одной системе координат (рис.1). В точках х1 и х2 значения обеих функций равна. Следовательно, х1 и х2 являются корнями уравнения ах2 = - (bх + с) и равносильного ему уравнения ах2 + bх + с = 0. Если парабола и прямая пересекаются, то квадратное уравнение имеет два равных корня. Если же парабола и прямая не пересекаются и не касаются, то квадратное уравнение не имеет корней. Уравнение ах2 + bх + с = 0 можно решить иначе, построив параболу y = ах2 + bх + с = 0 и, найдя точки ее пересечения с осью Ох, если D≥0 (рис. 2).
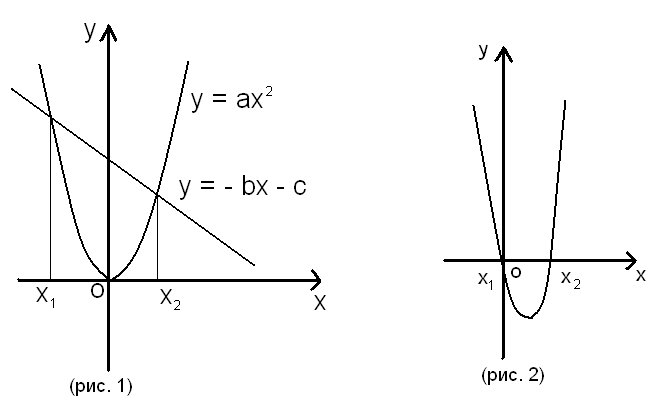
Решим уравнение 4х2 - 16х + 15 = 0.
Преобразуем уравнение к виду 4х2 = 16х - 15
Построим в одной системе координат графики функций y = 4х2– параболу и
y = 16х - 15 – прямую (рис.3)
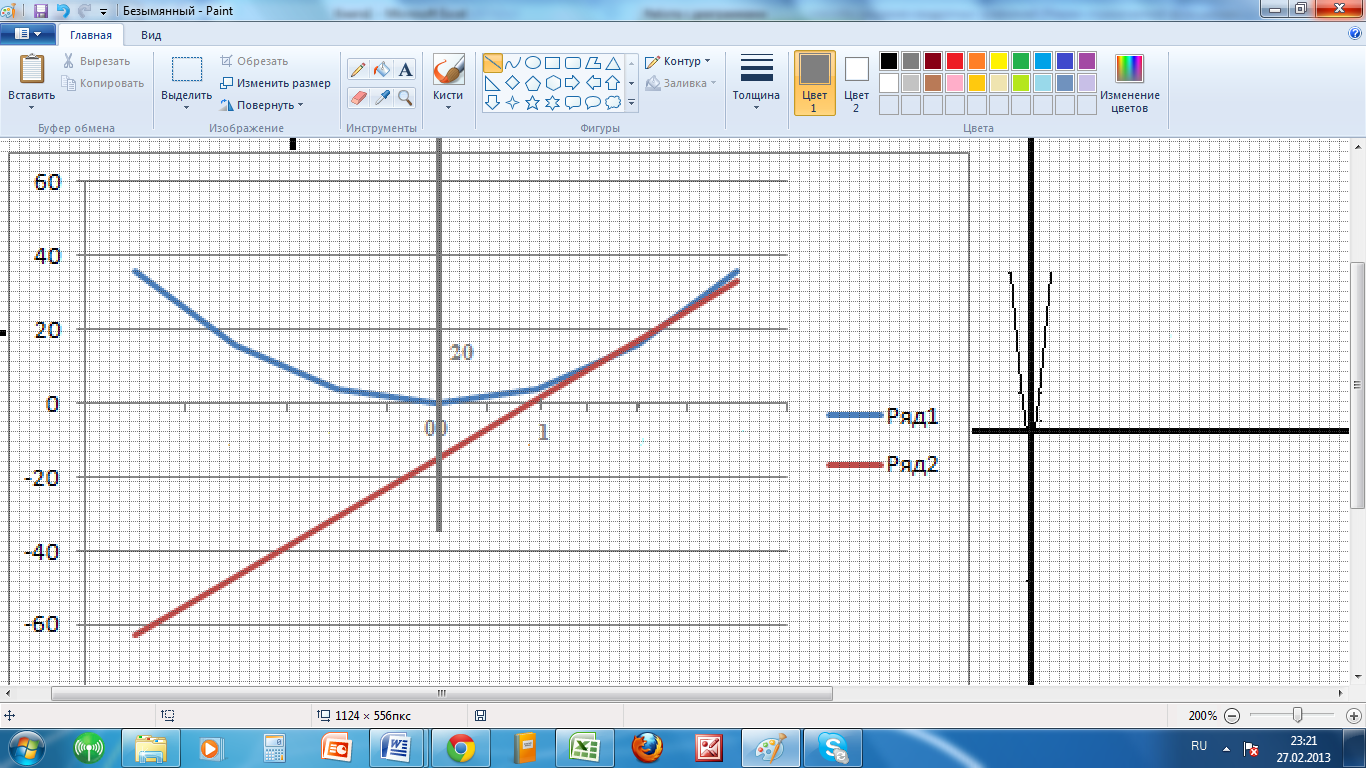
(Рис.3)
Ответ:1,5;2,5.
7) Решение квадратных уравнений с помощью циркуля и линейки
П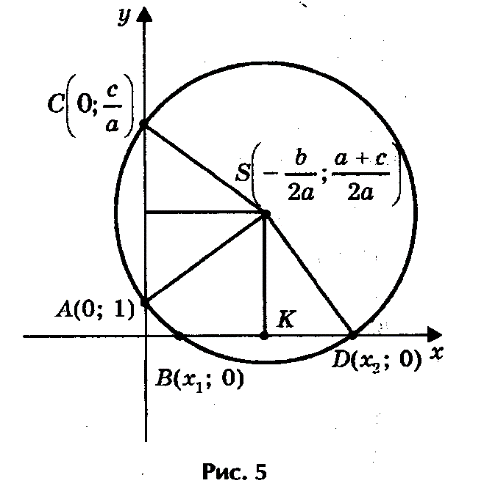 редлагаю следующий способ нахождения корней квадратного уравнения ах2 + bх + с = 0 с помощью циркуля и линейки (рис.5).Допустим, что искомая окружность пересекает ось абсцисс в точках В(х1; 0 ) и D (х2; 0), где х1 и х2 - корни уравнения ах2 + bх + с = 0, и проходит через точки А(0; 1) и С(0; c/a) на оси ординат. Тогда по теореме о секущих имеем OB·OD = OA·OC, откуда OC = OB ·OD/ OA= х1х2/ 1 = c/a. Центр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд ACи BD, поэтому
редлагаю следующий способ нахождения корней квадратного уравнения ах2 + bх + с = 0 с помощью циркуля и линейки (рис.5).Допустим, что искомая окружность пересекает ось абсцисс в точках В(х1; 0 ) и D (х2; 0), где х1 и х2 - корни уравнения ах2 + bх + с = 0, и проходит через точки А(0; 1) и С(0; c/a) на оси ординат. Тогда по теореме о секущих имеем OB·OD = OA·OC, откуда OC = OB ·OD/ OA= х1х2/ 1 = c/a. Центр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд ACи BD, поэтому 
И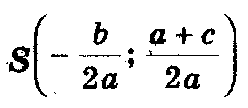 так:
так:
1) построим точки S- (центр окружности) и A(0; 1);
2) проведем окружность с радиусом SA;
3) абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.
При этом возможны три случая.
1) Радиус окружности больше ординаты центра (ASSK, или Ra + c/2a), окружность пересекает ось Ох в двух точках (рис. 6а) В(х1; 0) и D(х2; 0), где х1 и х2 - корни квадратного уравнения ах2 + bх + с = 0.
2) Радиус окружности равен ординате центра (AS = SB, или R = a + c/2a), окружность касается оси Ох (рис.6б) в точке В (х1; 0), где х1 - корень квадратного уравнения.
3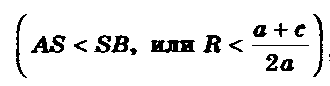 ) Радиус окружности меньше ординаты центра
) Радиус окружности меньше ординаты центра
окружность не имеет общих точек с осью абсцисс (рис. 6в), в этом случае уравнение не имеет решения.(Рис.6):
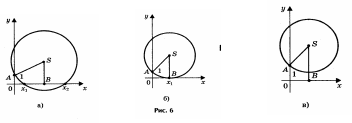 а) б) в)
а) б) в)

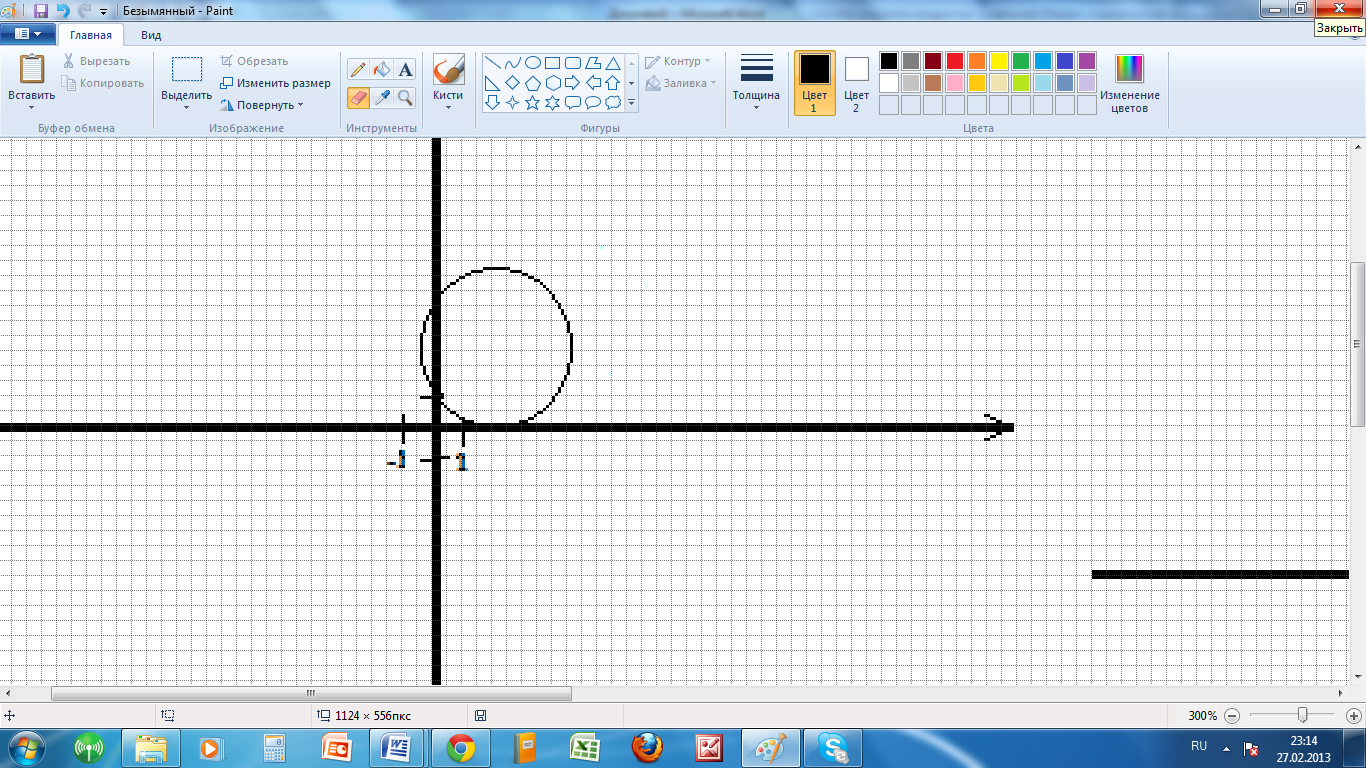
Решим уравнение 4х2 - 16х + 15 =0(рис.7).
Решение. Определим координаты точки центра
окружности по формулам:
�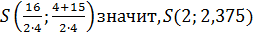 �(Рис.7)
�(Рис.7)
проведем окружность радиуса SA, где А (0; 1).
Ответ:1,5; 2,5.
8) Геометрический способ решения квадратных уравнений. В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. Приведу ставший знаменитым пример из «Алгебры» ал - Хорезми.
Решим уравнение х2 + 10х = 39.
В оригинале эта задача формулируется следующим образом: «Квадрат и десять корней равны 39»
Решение. Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2,5, следовательно, площадь каждого равна 2,5х. Полученную фигуру дополняют затем до нового квадрата ABCD, достраивая в углах четыре равных квадрата, сторона каждого их них 2,5, а площадь 6,25.
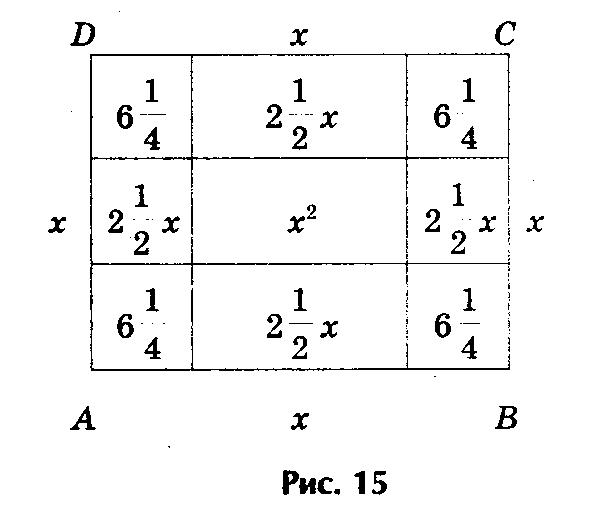
Площадь S квадрата ABCD можно представить, как сумму площадей: первоначального квадрата х2, четырех прямоугольников (4· 2,5х = 10х) и четырех пристроенных квадратов (6,25· 4 = 25), т.е. S =х2 + 10х + 25. Заменяя х2 + 10х числом 39, получим, что S = 39 + 25 = 64, откуда следует, что сторона квадрата ABCD, т.е. отрезок АВ = 8. Для искомой стороны х первоначального квадрата получим
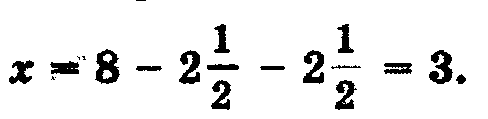
9) Приведение к виду (f(x))2=(g(x))2.
Путем преобразований уравнение приводится к виду (kx)2=(mx±n)2.
Пример: �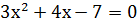 �, | :7
�, | :7
�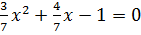 �,
�,
�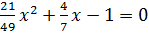 �,
�,
�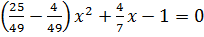 �,
�,
�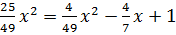 �,
�,
�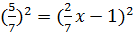 �,
�,
�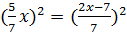 �,
�,
|5x|=|2x-7|,
1)5x=2x-7, 2)5x=7-2x,
5x-2x=-7, 5x+2x=7,
3x=-7, 7x=7,
x=�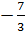 �, x=1.
�, x=1.
10) Уменьшение степени уравнения (использование теоремы Безу). Данный способ широко применяется при решении алгебраических уравнений высших степеней.
Теорема Безу. При делении многочлена n-й степени относительно x на двучлен x-a остаток равен значению делимого при x=a.
Следствие из теоремы Безу. Если уравнение а0хn + a1xn-1+ … + an-1x+an = 0, где все коэффициенты целые, имеет целые корни, то это делители свободного члена.
Пример:�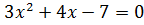 �,
�,
�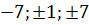 �,
�,
�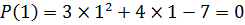 �,
�,
�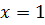 �,
�,
�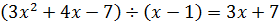 �,
�,
�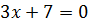 �,
�,
�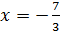 �.
�.
11) Разложение на множители способом группировки. При решении квадратных уравнений часто применяется метод разложения на множители (с помощью вынесения за скобки общего множителя, формул сокращенного умножения или способа группировки).
Пример:�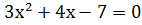 �,
�,
�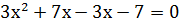 �,
�,
� �,
�,
�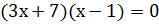 �,
�,

РАЗДЕЛ II. Практическая часть
2.1. Решение уравнений из второй части ОГЭ
Проанализировав контрольно-измерительные материалы ОГЭ, я пришел к выводу, что для успешного решения уравнений из второй части экзамена необходимо знать следующие способы решения уравнений: разложение на множители способом группировки, замена переменной, извлечение корней кубической степени, разложение на множители с помощью формулы разности квадратов, решение уравнений с учетом ОДЗ, решение квадратных уравнений, решение линейных уравнений, уравнение с параметром, решение рациональных уравнений.
В данном разделе мною разбиты на группы все уравнения второй части из ОГЭ и приведены их решения.
1. Решение уравнений разложение на множители способом группировки.
Для обучающихся 8 класса я провел занятие по способам решений уравнений. Для своих одноклассников подготовил памятку, разработал домашнее задание на отработку решений уравнений второй части ОГЭ (см. Приложение 1) и предложил своим одноклассникам решить уравнения более повышенного уровня (см. Приложение 2).
2.2. Решение уравнений нестандартными способами
1. Уравнение третьей степени, в стандартном виде. Метод решения – разложения на линейные множители (теорема Безу):
x³ + x² + 11x – 21 = 0.
Так как это уравнение рациональное целое с целыми коэффициентами, то оно имеет целые корни, являющиеся делителями свободного члена: 21: 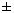 1;
1; 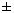 3;
3; 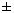 7;
7; 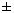 21. x1 = 1 является корнем (убеждаемся подстановкой), поэтому многочлен левой части уравнения делится на двучлен х – 1.
21. x1 = 1 является корнем (убеждаемся подстановкой), поэтому многочлен левой части уравнения делится на двучлен х – 1.
(x3 + 9x2 + 11x – 21) : (x – 1) = x2 + 10x + 21;
x3 + 9x2 + 11x – 21 = (x – 1)(x2 + 10x + 21).
Решим уравнение x² + 10x + 21 = 0. По теореме Виета корни:
x2 = –3, x3 = –7, x1 = 1.
Ответ: {–7; –3; 1}.
2. x(x + 1)(x – 1)(x + 2) = 24.
Это уравнение четвертой степени. Метод решения – группировка. Если левая часть уравнения представлена в виде разложения на линейные множители, а в правой – число и выносящиеся: (x + a)(x + b)(x + b)(x + c) = A и a + b = c + d, в этом случае возможна группировка множителей.
(x(x + 1))*((x – 1)(x + 2)) = 24;
(x² + x)*(x² + x – 2) = 24.
Сделаем замену x² + x = t и получим уравнение
t(t – 2) – 24 = 0,
t2 – 2t – 24 = 0.
Корни по теореме Виета: t1 = 6, t2 = –4.
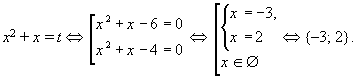
Ответ: {–3; 2}.
3. 5 – 12x³ + 14x² = 12x – 5, 5x² – 12x³ + 14x² – 12x + 5 = 0 – возвратное уравнение членов степени. Так как x = 0 не является корнем данного уравнения, разделим почленно на x² и сгруппируем: 
Сделаем замену: 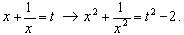
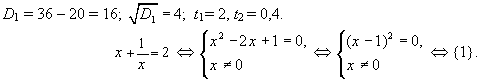
Ответ: {1}.
4. 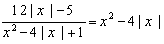 – это дробно-рациональное уравнение, содержащее модуль.
– это дробно-рациональное уравнение, содержащее модуль.
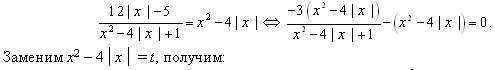
Заменим x2 – 4│х│ = t, получим:
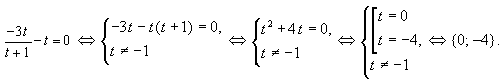
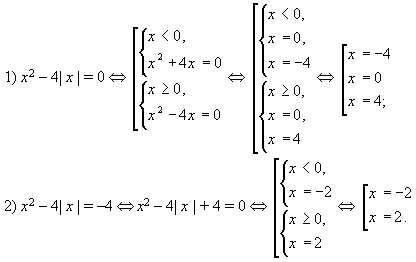
Ответ: {0; 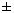 2;
2; 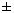 4}
4}
Алгоритм: а) находим нули модуля; б) дискриминант уравнения разбиваем на промежутки; в) раскрываем модуль на каждом из промежутков; г) выбираем ответ, учитывая данный промежуток; д) ответ – совокупность решений.
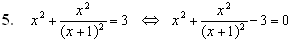 – это дробно-рациональное уравнение. Выделим квадрат разности:
– это дробно-рациональное уравнение. Выделим квадрат разности:
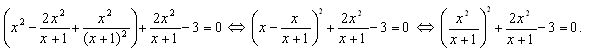
Введем новую переменную 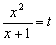 и получим уравнение вида t² + 2t – 3 = 0. По теореме Виета корни этого уравнения t = 1 или t = –3.
и получим уравнение вида t² + 2t – 3 = 0. По теореме Виета корни этого уравнения t = 1 или t = –3.
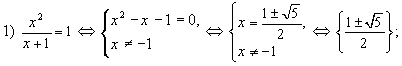
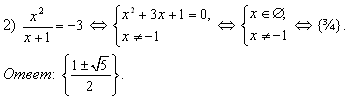
6. ax² + 3ax – (a + 2) = 0 – это квадратное уравнение с параметром. При решении уравнения с параметрами необходимо выяснить, при каких значениях параметров уравнение имеет корни и сколько их в зависимости от параметров при которых это выражение действительно определяет корни уравнения, то есть найти при каком значении параметра:  г) x – единственный корень.
г) x – единственный корень.
Решение:
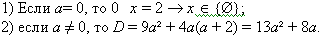
При D 0 уравнение имеет два различных действительных корня, то есть при
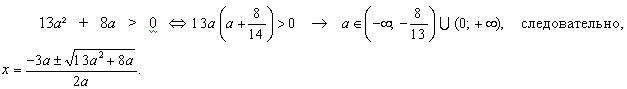
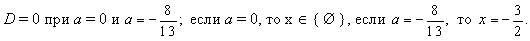
При D
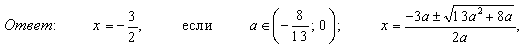
если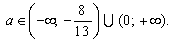
Заключение
На основании всего выше изложенного можно сделать вывод, что уравнения необходимы в современном мире не только для решения практических задач, но и в качестве научного инструмента. Поэтому так много ученых изучали этот вопрос и продолжают изучать.
Человечество прошло длительный путь от незнания к знанию, непрерывно заменяя на этом пути неполное и несовершенное знание всё более полным и совершенным. В ходе выполнения своей исследовательской работы я считаю, что с поставленной целью и задачами я справился, мне удалось обобщить и систематизировать изученный материал по выше указанной теме.
Выполненная работа показывает, что использование различных способов при решении уравнений является важным звеном в изучении математики, развивает внимание и сообразительность. Также не менее важно умение правильно выбирать рациональный способ решения конкретно для каждого уравнения.
В процессе работы над проектом, была создана система нестандартных приемов решения уравнений и разработано домашнее задание, на основе которого проведена успешная апробация этих приемов. Данный материал можно рекомендовать для внеклассных, элективных и факультативных занятий по математике. Учителя могут использовать его как методическое пособие при изучении темы «Решение уравнений», а также, для организации подготовки к ОГЭ. Материалом этого проекта могут воспользоваться и те, кто любит математику, и те, кто сдает экзамен по математике.
23
Решая уравнения разными способами, я понял, что есть способы удобные в применении, а есть неудобные или скорее непривычные. Более рациональные способы для решения уравнений – это способы, которые предлагаются в учебниках алгебры, но они не всегда рациональны. Некоторые способы решения такие, как применение теоремы Виета и свойство коэффициентов помогают сэкономить время, что немаловажно при решении заданий на контрольных работах и экзаменах. Самым неудобными способами для меня показались – графический, геометрический и с помощью циркуля и линейки.
Список используемой литературы
1. Ван дер Варден Б.А. Пробуждающаяся наука. Математика древнего Египта, Вавилона и Греции. [Текст] Б.А. Ван дер Варден - М., ГИФМЛ, 1959. - 462 с.
2. Гельфман Э.Г. Квадратные уравнения. [Текст] Э.Г. Гельфман - Москва, 1997. 273с.
3. ГлейзерГ.И. История математики в школе/ Г.И.Глейзер-М.: Просвещение, 1982- 340с.
4. Плужников И. Десять способов решения квадратных уравнений// Математика в школе. -2000.-№40
5. http://revolution.allbest.ru/
6. http://mat.1september.ru/2001/42/no42_01.htm
7. Википедия https://ru.wikipedia.org/wiki/%D0%A3%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5
8. Сведения из истории уравнений https://sites.google.com/site/vmireuravnenij/svedenia-iz-istorii-uravnenij
9. https://f55dc317-a-62cb3a1a-s-sites.googlegroups.com/site/vmireuravnenij/svedenia-iz-istorii uravnenij/%D0%94%D0%B8%D0%BE%D1%84%D0%B0%D0%BD%D1%82.gif?attachauth=ANoY7cqWwgeBYnJcoYYvidAVCZMKAobdZvppTQ5XkdmLeNqpQ8YCJQdb49zunJEcWNbj9xERYhUqqyP4_R0bcLVMrfD8guSGMrWceKnXfeIb5Kwg8kKkkKJwRS3NNd3qIrkgeadCODBGorikyX6dWx2PBsxmFvA5_ae9ptTL_Cz9A72Fn4lRXVULxrdbF5WZbIWYKmBtovRgrfeYW6GREKk7jpKL7lEiCm4NhyUJ50A1yDA3-XnlVQlqb6GQPG_D9AYOpmoYsg7OFH7B3eYzwA5v-UOuJ6Kvwg8ctqCq-oEQGwKbDT_tpXY%3D&attredirects=0
10. https://math-oge.sdamgia.ru/
Приложение 1. Дидактический материал
по решению уравнений второй части ОГЭ
Решите уравнение 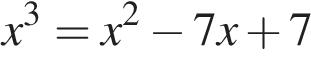 .
.
Решите уравнение (x − 2)(x − 4)(x − 6) = (x − 4)(x − 5)(x − 6).
Решите уравнение (х + 7)3 = 49(x + 7).
Решите уравнение (x − 1)(x2 + 4x + 4) = 4(x + 2).
5. Решите уравнение 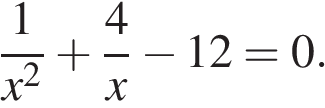
6. Решите уравнение 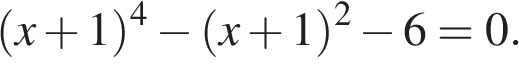
Решите уравнение x6 = (6x − 8)3.
Решите уравнение 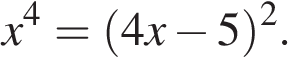
Решите уравнение 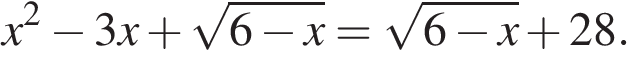
Решите уравнение 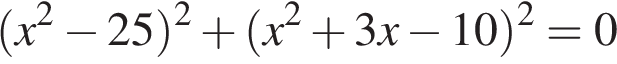 .
.
11. Решите уравнение 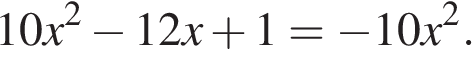
Приложение 2. Дидактический материал
по решению уравнений более сложного уровня
1. Решить уравнение x³ – 5x² + 5x + a = 0, если известно, что один из его корней равен 1.
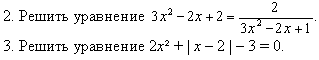
4. Решить уравнение 78x4 – 133х³ + 48х² – 133х + 78 = 0.
5. Для каждого значения параметра а решить уравнение ax² – (2a + 7)x + a + 3 = 0.
6. Найдите все значения параметра b, при которых уравнение 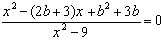 имеет ровно один корень.
имеет ровно один корень.
7*. Решить уравнение x4 + 4х + 3 = 0.

















 редлагаю следующий способ нахождения корней квадратного уравнения ах2 + bх + с = 0 с помощью циркуля и линейки (рис.5).Допустим, что искомая окружность пересекает ось абсцисс в точках В(х1; 0 ) и D (х2; 0), где х1 и х2 - корни уравнения ах2 + bх + с = 0, и проходит через точки А(0; 1) и С(0; c/a) на оси ординат. Тогда по теореме о секущих имеем OB·OD = OA·OC, откуда OC = OB ·OD/ OA= х1х2/ 1 = c/a. Центр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд ACи BD, поэтому
редлагаю следующий способ нахождения корней квадратного уравнения ах2 + bх + с = 0 с помощью циркуля и линейки (рис.5).Допустим, что искомая окружность пересекает ось абсцисс в точках В(х1; 0 ) и D (х2; 0), где х1 и х2 - корни уравнения ах2 + bх + с = 0, и проходит через точки А(0; 1) и С(0; c/a) на оси ординат. Тогда по теореме о секущих имеем OB·OD = OA·OC, откуда OC = OB ·OD/ OA= х1х2/ 1 = c/a. Центр окружности находится в точке пересечения перпендикуляров SF и SK, восстановленных в серединах хорд ACи BD, поэтому 
 а) б) в)
а) б) в)