Вписанные и описанные окружности

Вписанные и описанные окружности

Подготовила Клянчина Дарина Проверила Музыкантова Елена Константиновна

2023

Содержание:

• Вписанная окружность.

• В многоугольнике.
• В треугольнике.

2. Описанная окружность.

• В многоугольнике.
• В треугольнике.

3. Задачи.

Вписанная и описанная окружность в треугольнике:

Окружность называют  вписанной  в угол, если она лежит внутри угла и касается его сторон. Центр окружности, вписанной в угол, лежит на биссектрисе этого угла.

Окружность называют описанной около треугольника, если все вершины треугольника расположены на окружности

Вписанная и описанная окружность в многоугольнике:

Если в данный выпуклый многоугольник можно вписать окружность, то биссектрисы всех внутренних углов данного многоугольника пересекаются в одной точке, которая является центром вписанной окружности.

Радиус вписанной в многоугольник окружности равен отношению его площади S к его полупериметру P:

r=S/P. Описанная окружность  многоугольника — окружность, содержащая все вершины многоугольника. Центром является точка (принято обозначать O) пересечения серединных перпендикуляров к сторонам многоугольника.

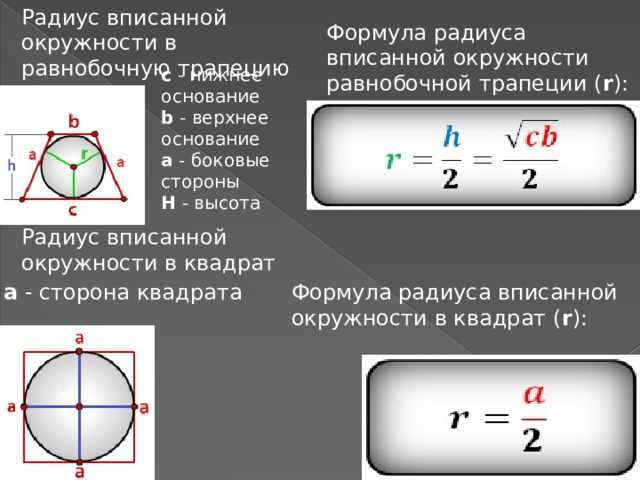
Радиус вписанной окружности в равнобочную трапецию

Формула радиуса вписанной окружности равнобочной трапеции ( r ):

с  - нижнее основание

b  - верхнее основание

a  - боковые стороны

H  - высота

Радиус вписанной окружности в квадрат

a  - сторона квадрата

Формула радиуса вписанной окружности в квадрат ( r ):

Радиус вписанной окружности в ромб

1.  Формулы радиуса вписанной окружности если известны: диагональ, стороны и угол

Формула радиуса вписанной окружности в ромб через диагональ и угол (  r  ) :

a  - сторона  ромба

D  - большая диагональ

d  - меньшая диагональ

α  - острый угол

О  - центр вписанной окружности

r  - радиус вписанной окружности

Формула радиуса вписанной окружности в ромб через диагонали (  r  ) :

Формула радиуса вписанной окружности в ромб через диагональ и сторону (  r  ) :

Формула радиуса вписанной окружности в ромб через сторону и угол (  r  ) :

2.  Радиус вписанной окружности ромба, равен половине его высоты

Формула радиуса вписанной окружности в ромб (  r  ) :

a  - сторона  ромба

h  - высота

О  - центр вписанной окружности

r  - радиус вписанной окружности

Формула радиуса вписанной окружности в правильный многоугольник, ( r ):

Радиус вписанной окружности в правильный многоугольник

a  - сторона многоугольника

N  - количество сторон многоугольника

Формула радиуса вписанной окружности в шестиугольник, ( r ):

Радиус вписанной окружности в шестиугольник

a  - сторона шестиугольника

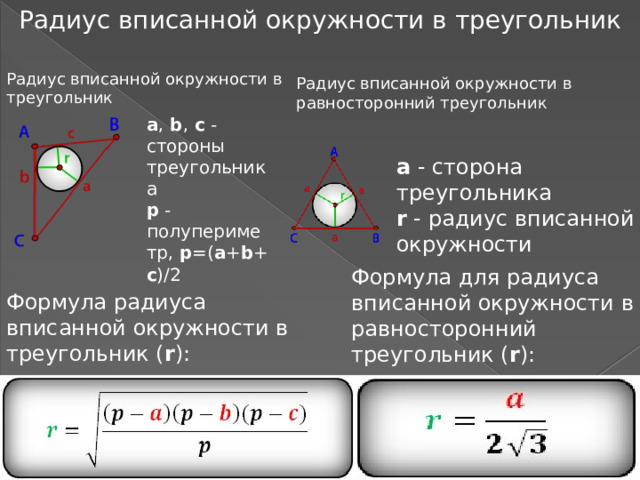
Радиус вписанной окружности в треугольник

Радиус вписанной окружности в треугольник

Радиус вписанной окружности в равносторонний треугольник

a ,  b ,  c  - стороны треугольника

p  - полупериметр,  p =( a + b + c )/2

a  - сторона треугольника

r  - радиус вписанной окружности

Формула для радиуса вписанной окружности в равносторонний треугольник ( r ):

Формула радиуса вписанной окружности в треугольник ( r ):

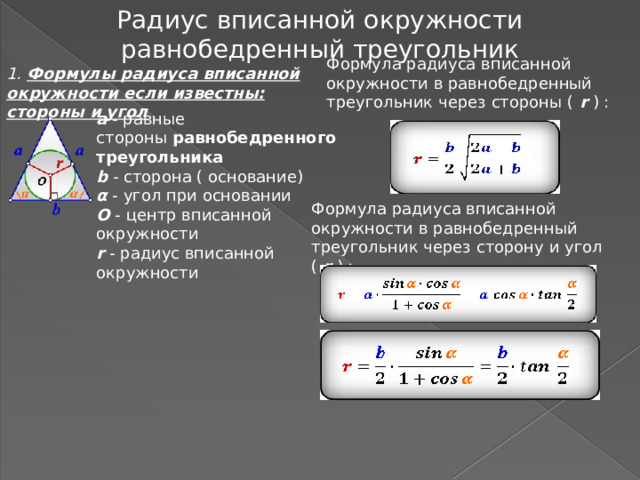
Радиус вписанной окружности равнобедренный треугольник

Формула радиуса вписанной окружности в равнобедренный треугольник через стороны (  r  ) :

1.  Формулы радиуса вписанной окружности если известны: стороны и угол

a  - равные стороны  равнобедренного треугольника

b  - сторона ( основание)

α  - угол при основании

О  - центр вписанной окружности

r  - радиус вписанной окружности

Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и угол (  r  ) :

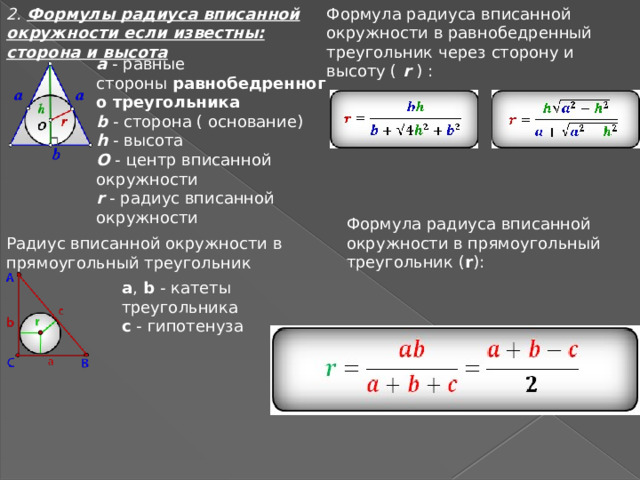
2.  Формулы  радиуса вписанной окружности  если известны: сторона и высота

Формула радиуса вписанной окружности в равнобедренный треугольник через сторону и высоту (  r  ) :

2.  Формулы радиуса вписанной окружности если известны: сторона и высота

a  - равные стороны  равнобедренного треугольника

b  - сторона ( основание)

h  - высота

О  - центр вписанной окружности

r  - радиус вписанной окружности

Формула радиуса вписанной окружности в прямоугольный треугольник ( r ):

Радиус вписанной окружности в прямоугольный треугольник

a ,  b  - катеты треугольника

с  - гипотенуза

Радиус описанной окружности трапеции по сторонам и диагонали

a  - боковые стороны трапеции

c  - нижнее основание

b  - верхнее основание

d  - диагональ

p  - полупериметр треугольника  DBC

p = (a+d+c)/2

Формула радиуса описанной окружности равнобокой трапеции, ( R )

Формула радиуса описанной окружности квадрата ( R )

Радиус описанной окружности квадрата равен половине его диагонали

a  - сторона квадрата

d  - диагональ

Радиус описанной окружности прямоугольника равен половине его диагонали

Формула радиуса описанной окружности прямоугольника ( R ):

a ,  b  - стороны прямоугольника

d  - диагональ

Радиус описанной окружности правильного многоугольника

Формула радиуса описанной окружности правильного многоугольника, ( R ):

a  - сторона шестиугольника

d  - диагональ шестиугольника

Радиус описанной окружности правильного шестиугольника

Радиус описанной окружности правильного шестиугольника ( R ):

a  - сторона многоугольника

N  - количество сторон многоугольника

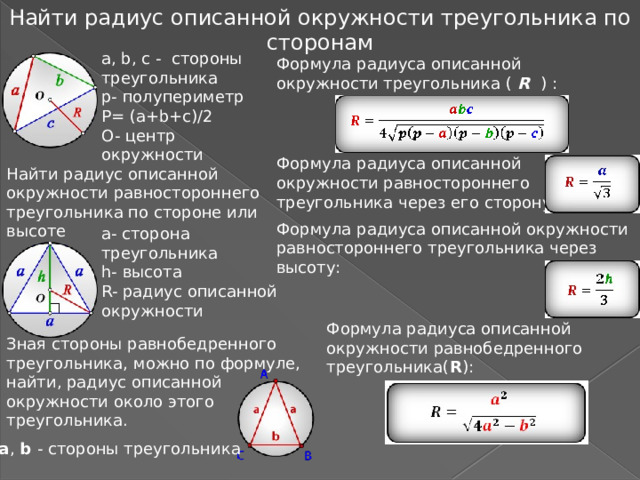
Найти радиус описанной окружности треугольника по сторонам

а, b, c -  стороны треугольника

p- полупериметр

P= (a+b+c)/2

O- центр окружности

Формула радиуса описанной окружности треугольника (  R    ) :

Формула радиуса описанной окружности равностороннего треугольника через его сторону:

Найти радиус описанной окружности равностороннего треугольника по стороне или высоте

Формула радиуса описанной окружности равностороннего треугольника через высоту:

а- сторона треугольника

h- высота

R- радиус описанной окружности

Формула радиуса описанной окружности равнобедренного треугольника( R ):

Зная стороны равнобедренного треугольника, можно по формуле, найти, радиус описанной окружности около этого треугольника.

a ,  b  - стороны треугольника

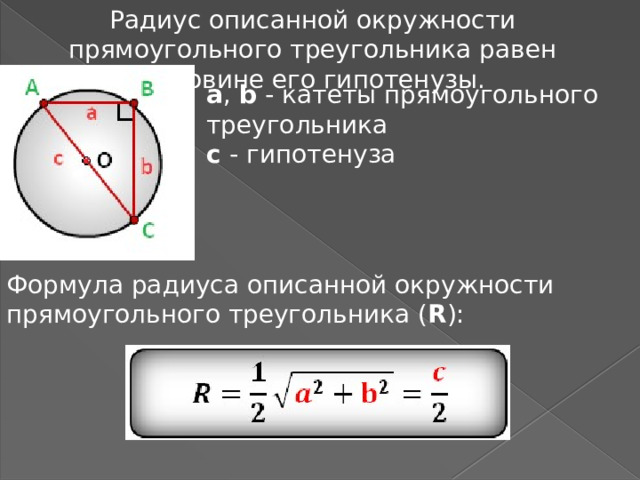
Радиус описанной окружности прямоугольного треугольника равен половине его гипотенузы.

a ,  b  - катеты прямоугольного треугольника

c  - гипотенуза

Формула радиуса описанной окружности прямоугольного треугольника ( R ):

Задачи:

Задача 1:

:

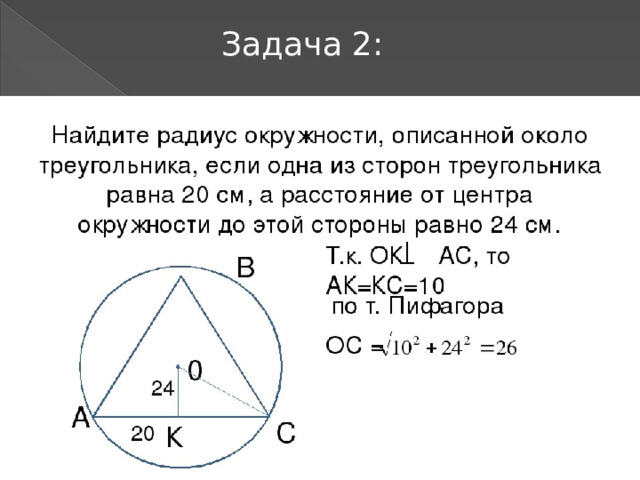
Задача 2:

Задача 3:

Задача 4:

Источники:

• https://www-formula.ru /
• https://infourok.ru /
• https://egemaximum.ru /
• https :// mavink.com/post/532D0C71B9B263E0CB19BBBE8F62EA571AAM1956B8
• http :// duckproxy.com/indexa.php?q=aHR0cDovL3d3dy5teXNoYXJlZC5ydS9zbG
• lkZS83Nzg5Nzcv
• https :// slide-share.ru/praktikum-12po-resheniyuplanimetricheskikh-zadachumk-lyuboj-201274
• https://www.yaklass.ru /

Спасибо за внимание!