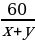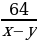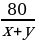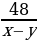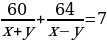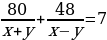Задачи на движение по реке, решаемые с помощью уравнения
При решении таких задач необходимо учитывать следующее:
За х принимаем или собственную скорость объекта (скорость в стоячей воде), или скорость течения реки.
Переменную х вводим в зависимости от условия задачи. Если известна скорость течения реки, то за х принимаем собственную скорость объекта. Если известна собственная скорость объекта, то за х принимаем скорость течения реки. Если неизвестны обе скорости, то вводим две переменные. Если обе скорости известны, то за х принимаем то, что неизвестно по условию задачи.
Составляем таблицу об объектах, о которых говорится в условии задачи
| Пояснения (объект, который движется) | Скорость, км/ч | Расстояние, км | Время, ч |
| По течению реки |
|
|
|
| Против течения реки |
|
|
|
| Плот |
|
|
|
| По озеру |
|
|
|
В таблице заполняем столбик «Скорость», учитывая, что
Скорость по течению = собственная скорость + скорость течения реки.
Скорость против течения = собственная скорость – скорость течения реки.
Скорость плота= скорости течения реки.
Скорость по озеру= собственной скорости объекта.
4) Заполняем по условию задачи еще один столбик
5) по таблице заполняем незаполненный столбик, учитывая
Время = расстояние : скорость
Расстояние = скорость * время
6) по последнему заполненному столбику составляем уравнение, учитывая условие задачи.
Рассмотрим примеры задач.
Задача 1. Спортивная лодка прошла расстояние 45 км против течения реки и такое же расстояние по течению реки, затратив на весь путь 14 ч. Определите собственную скорость лодки, если скорость течения реки 2 км/ч
Решение.
Пусть х км/ч собственная скорость лодки
Таблица
| Спортивная лодка | Скорость, км/ч | Расстояние, км | Время, ч |
| По течению реки | Х+2 | 45 | 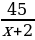
|
| Против течения реки | Х-2 | 45 | 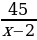
|
По условию задачи спортивная лодка на путь по течению и на путь против течения затратила 14 часов. Составим и решим уравнение.
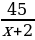 +
+ 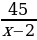 = 14.
= 14.
х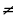 2, х
2, х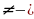 2
2
45(х-2) + 45(х+2) = 14(х-2)(х+2),
45х-90 + 45х +90 = 14(х2 -4),
90х=14(х2 -4),
45х=7(х2 -4),
7х2 -45х- 28=0,
Д= 2809,
х1=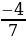 , х2=7.
, х2=7.
По смыслу задачи, скорость величина положительная, этому условию удовлетворяет число 7. Итак, собственная скорость спортивной лодки 7 км/ч.
Ответ: 7 км/ч
Задача 2. Лодка может проплыть 18 км по течению реки и еще 2 км против течения за то же время, какое потребуется плоту, чтобы проплыть 8 км по этой реке. Найдите скорость течения реки, если известно, что собственная скорость лодки 8 км/ч.
Решение.
1Пусть х км/ч скорость течения реки
Таблица
|
| Скорость, км/ч | Расстояние, км | Время, ч |
| Лодка по течению реки | 8+х | 18 | 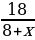
|
| Лодка против течения реки | 8-х | 2 | 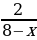
|
| Плот | х | 8 | 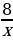
|
По условию задачи время лодки в пути и плота одно и то же. Составим и решим уравнение.
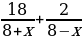 =
= 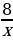
х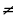 8, х
8, х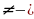 8. х
8. х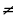 0,
0,
18х(8-х) +2х(8+х)= 8(8-х)(8+х),
9х(8-х) +х(8+х)= 4(64-х2),
72х – 9х2 +8х+ х2= 256 – 4х2.
4х2 -80х +256= 0,
х2 – 20х+ 64= 0,
х1=4, х2 = 16.
Оба корня удовлетворяют уравнению. По смыслу задачи скорость течения реки должна быть меньше собственной скорости лодки, этому условию удовлетворяет число 4. Итак, скорость течения реки 4 км/ч .
Ответ: 4 км/ч
Задача 3. Группа туристов отправляется на лодке от лагеря по течению реки с намерением вернуться обратно через 5 часов. Скорость течения реки 2 км/ч, собственная скорость лодки 8 км/ч. На какое наибольшее расстояние по реке они могут отплыть, если перед возвращением планируют пробыть на берегу 3 час?
Решение.
Пусть на х км группа туристов может отплыть по реке.
2) Таблица
| Группа туристов | Скорость, км/ч | Расстояние, км | Время, ч |
| По течению реки | 8+2=10 | х | 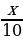
|
| Против течения реки | 8-2=6 | х | 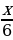
|
По условию задачи группа туристов должна вернуться назад через 5 часов, затратив время на движение по течению реки и против течения реки и отдых на берегу 3 часа. Составим и решим уравнение
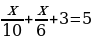 ,
, 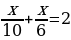 ,
,
3х+5х= 60,
8х=60,
2х=15,
х=7,5
На 7,5 км группа туристов может отплыть по реке.
Ответ 7,5 км
Задача 4. За 7 часов катер прошел 60 км по течению реки и 64 км против течения. В другой раз катер за 7 часов прошел 80 км по течению реки и 48 км против течения. Определите собственную скорость катера и скорость течения реки.
Решение.
Пусть х км/ч собственная скорость лодки, у км/ч – скорость течения реки
Таблица
| Катер | Скорость, км/ч | Расстояние, км | Время, ч |
| В первый раз |
|
|
|
| По течению реки | х+у | 60 | 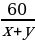
|
| Против течения реки | х-у | 64 | 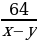
|
| Во второй раз |
|
|
|
| По течению реки | х+у | 80 | 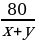
|
| Против течения реки | х-у | 48 | 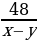
|
По условию задачи катер в первый раз на путь по течению и на путь против течения затратил 7 часов. Получим уравнение
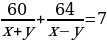
Катер во второй раз на путь по течению и на путь против течения затратил 7 часов. Получим уравнение
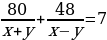
Составим и решим систему уравнений.
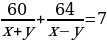
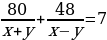
Ответ:18 км/ч; 2 км/ч







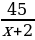
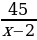
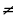 2, х
2, х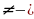 2
2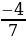 , х2=7.
, х2=7.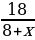
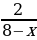
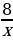
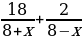 =
= 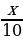
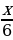
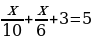 ,
, 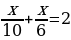 ,
,